Énergie potentielle mécanique

L'énergie potentielle mécanique est une énergie qui est échangée par un corps lorsqu'il se déplace tout en étant soumis à une force conservative.

Elle est exprimée en joules (c'est-à-dire en newton mètre, ou kg m² s⁻²). Cette énergie potentielle, définie à une constante arbitraire près, ne dépend que de la position du corps dans l'espace. Elle est appelée potentielle car elle peut être emmagasinée par un corps et peut ensuite être transformée par exemple en énergie cinétique lorsque le corps est mis en mouvement.

De manière plus précise, la variation d'énergie potentielle d'un corps lorsqu'il se déplace entre deux points est l'opposé du travail fourni par la force à laquelle il est soumis entre ces deux points.

Ainsi le travail d'une force conservative vérifie la relation:

$\mathrm {\delta } W_{F}=-\mathrm {d} E_{p}$

Un exemple simple est celui d'un corps terrestre tenu en hauteur (et donc possédant une énergie potentielle de pesanteur du fait de sa hauteur) qui, une fois lâché, transforme cette énergie potentielle en énergie cinétique quand sa vitesse augmente lors de sa chute.

Généralités

Chaque force conservative donne naissance à une énergie potentielle. On peut ainsi distinguer :

• énergie potentielle de pesanteur,
• énergie potentielle gravitationnelle,
• énergie potentielle élastique,
• énergie potentielle électrostatique,
• énergie potentielle magnétique,
• énergie potentielle d'inertie d'entraînement (dans certaines situations simples),
• énergie potentielle de pression.

L'énergie potentielle est définie à une constante additive près. Celle-ci n'a aucune influence sur les résultats puisque l'énergie potentielle est utilisée dans des opérations de dérivation (calcul d'une force conservative) ou de variation (calcul d'un travail). Ces deux opérations faisant disparaître la constante, le choix de cette dernière est donc purement arbitraire et sa détermination se fait généralement de façon à simplifier les calculs.

Utilisation de l'énergie potentielle

Le calcul de l'énergie potentielle puis l'utilisation de l'expression de l'énergie mécanique peut permettre la détermination de l'équation du mouvement du système. Cette méthode est souvent plus judicieuse que l'utilisation du principe fondamental de la dynamique.

Méthode énergétique pour la résolution du mouvement du pendule simple

Dans le cas du mouvement du pendule simple, on a comme paramètre $\theta$, l'angle que fait le pendule avec la verticale, et l, la longueur du fil.

On se place dans le repère polaire $(0,{\vec {U_{r}}},{\vec {U_{\theta }}})$. Le système considéré est la masse $m$ dans le référentiel galiléen.

Pendule simple.

• L'énergie cinétique du système vaut :

$E_{c}={\frac {1}{2}}ml^{2}{\dot {\theta }}^{2}$

• L'énergie potentielle de pesanteur vaut, à une constante près :

$E_{pe}=-mgl\cos(\theta )+{\text{cste}}\!$

En choisissant cette constante nulle, on obtient :

$E_{pe}=-mgl\cos(\theta )\!$

• On calcule ensuite le travail dissipé par la force de tension ${\vec {T}}$:

$\mathrm {\delta } W_{T}={\vec {T}}\cdot {\vec {\mathrm {d} r}}=-T\cdot {\vec {U_{r}}}\cdot l\,\mathrm {d} \theta \cdot {\vec {U_{\theta }}}=0$

La tension du fil étant normale au mouvement de la masse m (on a supposé le fil tendu pendant le mouvement, donc la vitesse purement orthoradiale), la force de tension du fil ne travaille pas. Ainsi, le système est uniquement soumis à des forces qui ne travaillent pas (${\vec {T}}$) et à des forces conservatives (le poids ${\vec {p}}$), et son énergie mécanique se conserve.

• On écrit l'expression de l'énergie mécanique :

$E_{m}=E_{c}+E_{pe}={\frac {1}{2}}ml^{2}{\dot {\theta }}^{2}-mgl\cos(\theta )$

L'énergie mécanique du système se conserve : on dit que cette énergie est conservative.

En dérivant par rapport au temps l'expression de l'énergie mécanique obtenue, on trouve :

$ml^{2}{\dot {\theta }}{\ddot {\theta }}+mgl\sin(\theta ){\dot {\theta }}=0$

Lorsque la vitesse angulaire ${\dot {\theta }}$ est non nulle, on peut simplifier l'équation sous la forme :

${\ddot {\theta }}+{\frac {g}{l}}\sin(\theta )=0$

Cette équation différentielle de second ordre décrit le mouvement du pendule simple.

Condition d'équilibre

À partir de la relation entre le travail et l'énergie potentielle on obtient la relation suivante, avec ${\vec {u}}$ le vecteur caractérisant le mouvement:

$\ \delta W_{F}={\vec {F}}\cdot {\vec {\mathrm {d} u}}=F\times \mathrm {d} u\times \cos({\widehat {fu}})=-\mathrm {d} E_{p}$

On a ainsi : $F\times \cos({\widehat {fu}})=-{\frac {\mathrm {d} E_{p}}{\mathrm {d} u}}$

Dans le cas où le système est soumis à cette seule force, on sait d'après les lois de Newton que le système est en équilibre si

${\vec {F}}={\vec {0}}$ (et le moment des forces est nul).

On en déduit une condition d'équilibre pour un système possédant une énergie potentielle :

${\frac {\mathrm {d} E_{p}}{\mathrm {d} u}}=0$

Puits d'énergie potentielle

Le système est donc en équilibre quand son énergie potentielle admet des minimums et des maximums locaux.

On peut alors différencier les positions d'équilibre stables et instables selon que l'énergie potentielle est respectivement minimale ou maximale. La stabilité d'un équilibre peut ainsi être déduite du signe de la dérivée seconde de l'énergie potentielle :

${\frac {\mathrm {d} ^{2}E_{p}}{\mathrm {d} u^{2}}}>0$ pour un équilibre stable (minimum de l'énergie potentielle), et a contrario ${\frac {\mathrm {d} ^{2}E_{p}}{\mathrm {d} u^{2}}}<0$ pour un équilibre instable (maximum de l'énergie potentielle).

On peut aussi soulever les notions de :

• puits d'énergie potentielle, lorsque le graphe de l'énergie potentielle en fonction du paramètre décrivant le mouvement admet un puits. Si le système n'a pas assez d'énergie mécanique pour sortir du puits, il est contraint de rester entre deux positions et peut éventuellement osciller ;
• barrière d'énergie potentielle, lorsque l'énergie potentielle tend vers l'infini quand le système s'approche d'une certaine position. Le système ne peut alors pas aller au-delà de cette position et est contraint de revenir en arrière.

Exemples

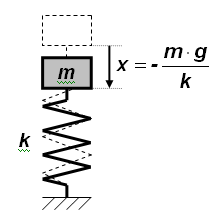
Considérons un système composé d'une masse m soumise à l'action de la gravité et suspendue à un ressort de raideur k. Dans ce cas, l'énergie potentielle du système est égale à la somme d'une énergie potentielle de pesanteur $m\,g\,x$ et d'une énergie potentielle élastique ${\frac {1}{2}}k\,x^{2}$ :

$E_{p}=m\,g\,x+{\frac {1}{2}}k\,x^{2}$

Énergie potentielle Énergie potentielle du système masse-ressort en fonction de la position de la masse

En considérant l'axe ${\vec {i}}$ vertical dirigé vers le haut, la condition d'équilibre donne alors :

${\vec {\nabla }}E_{p}={\frac {\mathrm {d} E_{p}}{\mathrm {d} x}}\,{\vec {i}}=(m\,g+k\,x)\,{\vec {i}}={\vec {0}}$

dont on déduit la condition d'équilibre :

$x=-{\frac {m\,g}{k}}$

Comme on peut le voir sur le graphique plus haut, cette position d'équilibre correspond au minimum strict de l'énergie potentielle du système, c'est donc une position d'équilibre stable (théorème de Lejeune Dirichlet).

Voir aussi

Articles connexes

• Énergie mécanique
• Énergie potentielle
• Énergie potentielle élastique
• Potentiel chimique