Référence (philosophie)
En philosophie du langage, la référence ou dénotation est l'objet dont parle un mot ou une expression. Par exemple l'expression « Astre du jour » fait référence à (ou désigne) l'objet auquel le mot « Soleil » fait également référence. Le mot « Soleil » n'est pas conceptuellement équivalent à l'expression « astre du jour », bien qu'ils réfèrent tous deux au même objet.
Le sens d’une expression se distingue alors de sa référence. Le sens est la manière dont est décrit son objet, tandis que la référence est l'objet décrit (ou le lien entre l'expression – ou un simple mot – et cet objet). Aujourd'hui, la plupart des philosophes du langage partagent l'idée selon laquelle la référence d'une phrase descriptive est ce qui permet de vérifier la description, mais ils se divisent sur le statut des noms propres.
L'histoire du concept de référence[modifier | modifier le code]
La référence directe chez John Stuart Mill[modifier | modifier le code]
Le philosophe John Stuart Mill argumenta que le sens d'un nom propre était sa référence. Il a décidé cela en remarquant que « Dartmouth » (littéralement « L'embouchure de la rivière Dart ») ne voulait pas dire « L'embouchure de la rivière Dart », par contre, même s'il n'y avait jamais eu de rivière auprès de 'Dartmouth', son sens serait la ville qu'il indique. Généralisant, il apparaît que le sens d'un nom propre est sa référence, et non pas une description associée au nom.
La référence indirecte chez Russell, Frege[modifier | modifier le code]
Des penseurs postérieurs ont critiqué cette analyse des noms propres, et ont développé des systèmes alternatifs. Ces systèmes ont été très influents, bien que l'œuvre récente de Kripke ait fait planer le doute sur eux.
La critique de Mill par Frege[modifier | modifier le code]
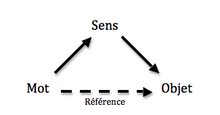
Frege a introduit la distinction entre la référence et le sens afin de résoudre le problème de la signification cognitive des mots. Par exemple, Frege a constaté qu'il est possible de ne pas savoir que « Éosphoros est Phosphoros », même si ces objets sont identiques. Ce ne serait pas possible si le sens des mots étaient leurs référents (comme le dit Mill). Il semble que Éosphoros et Phosphoros n'ont pas le même sens même s'ils ont le même référent, d'où il suit que le sens et la référence d'un mot ne sont pas identiques. Le sens de Éosphoros c'est « première lueur vue à l'aube », alors que le sens de Phosphoros c'est « porteur de lueur », bien que la référence de chaque mot soit Vénus.
La formalisation de Frege par Russell[modifier | modifier le code]
La théorie du langage de Bertrand Russell, tributaire de l'œuvre de Frege, était une théorie de la référence indirecte. Ce dernier distinguait d'abord entre une « référence » et un « sens ». Le référent ou la référence est l'objet dans le monde réel ; le sens est la description ou le concept qui est subjectivement lié au mot.
Russell s'intéressait aux descriptions définies (p. ex. la table) et indéfinies (p. ex. une table). Selon Russell, il fallait retrouver la forme logique de ces énoncés, ce qu'il faisait en transformant, à l'aide de quantificateurs existentiels, les descriptions définies en descriptions indéfinies.
Ainsi, la proposition « le roi de France est chauve », était traduite par Russell, en termes logiques clarifiant sa signification :
- La clause ontologique : il existe un x qui est roi de France ;
- La clause d'unicité : il n'y a qu'un seul x qui soit tel ;
- L'assertion : et x est chauve.
L'article défini disparaît ainsi de la description définie telle que retranscrite par Russell, étant diffusée dans l'ensemble de la proposition.
Russell critique explicitement Frege sur l’idée que “le roi de France” est chauve “devrait être dépourvu de sens; mais elle n’est pas dépourvue de sens[1] , puisqu’elle est tout simplement fausse”. En réalité, Frege ne dit pas qu’une proposition comportant un terme vide est dépourvue de sens, seulement qu’elle est dépourvue de dénotation.(« l'actuel roi de France »). Or, Russell montre que cet énoncé est faux, mais n'est pas dépourvu de vérité. Autrement dit, des expressions telles que « l'actuel roi de France » ou la « montagne d'or » ne nous obligent pas à postuler des entités inexistantes, comme le croyait Russell lui-même dans les Principes de la mathématique, ni à violer le principe du tiers exclu[1].
La transcription logique de la forme grammaticale d'une description définie sous forme d'une description indéfinie peut aussi être faite pour un nom propre[1]. Or, pour Russell, des noms tels que Socrate ou Pégase ne sont pas des noms logiquement propres[1] : ce sont en réalité des abréviations de descriptions (le philosophe qui est mort à Athènes, etc.). En effet, les seuls noms propres, au sens logique, sont pour Russell les concepts qui s'appliquent « à un individu dont le locuteur a une connaissance directe acquaintance. » [1]. Les autres noms propres, grammaticaux, sont des abréviations de descriptions, qui ne décrivent pas un individu (particular) mais un « système compliqué de classes et de séries ».
La description définie de « le roi de France est chauve » peut aussi être exprimée sous une forme logique plus stricte, comme suit :
On lit donc : « Il existe un x tel que : x est roi de France ; et pour tout y qui est roi de France, cet y est x ; et x est chauve. »
Notes et références[modifier | modifier le code]
- Russell, The Philosophy of Logical Atomism, traduit in Ecrits de logique philosophique, cité par D. Marconi, ibidem.


