Polynôme de Jones
Le polynôme de Jones en théorie des nœuds est un invariant polynomial des nœuds (incomplet) introduit par Vaughan Jones en 1984. Plus précisément, c'est un invariant d'un nœud orienté ou d'un entrelacs orienté, qui est un polynôme de Laurent à coefficients entiers en la variable .
Propriétés[modifier | modifier le code]
Le polynôme de Jones est caractérisé par le fait qu'il prend la valeur 1 pour le nœud trivial et vérifie la « relation d'écheveau (en) » (skein relation) suivante :
où , et sont des diagrammes d'entrelacs orientés qui ne diffèrent que dans une petite région de la façon suivante
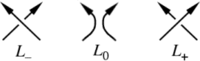
Le polynôme de Jones, contrairement au polynôme d'Alexander, permet parfois de distinguer un nœud de son image par un miroir. Si est l'image du nœud par un miroir, on a la relation suivante :
- .
Le polynôme de Jones du nœud de trèfle est .
Bibliographie[modifier | modifier le code]
- (en) Louis Kauffman, « State models and the Jones polynomial », Topology, vol. 26, no 3, , p. 395-407










