« Cryptographie sur les courbes elliptiques » : différence entre les versions
mAucun résumé des modifications |
Ϛ (discuter | contributions) reprise intégrale :) |
||
| Ligne 2 : | Ligne 2 : | ||
[[File:Adding P,Q.PNG|vignette|alt=addition de points|Additions de points sur une courbe elliptique]] |
[[File:Adding P,Q.PNG|vignette|alt=addition de points|Additions de points sur une courbe elliptique]] |
||
La '''cryptographie sur les courbes elliptiques''' regroupe un ensemble de techniques [[Cryptographie|cryptographiques]] qui utilisent une ou plusieurs propriétés des [[Courbe elliptique|courbes elliptiques]], ou plus généralement d'une [[variété abélienne]]. L'usage des courbes elliptiques en cryptographie a été suggéré, de manière indépendante, par [[Neal Koblitz]] et [[Victor Miller]] en [[1985]]<ref>{{article|langue=en|auteur=Neal Koblitz|titre=Elliptic curve cryptosystems|périodique=Mathematics of Computation|numéro=48|année=1987|pages=203-209|doi=10.1090/S0025-5718-1987-0866109-5}}.</ref>{{,}}<ref>{{article|langue=en|auteur=Victor S. Miller|titre=Use of elliptic curves in cryptography|périodique=Crypto|volume=218|pages=417-426|année=1985|doi=10.1007/3-540-39799-X_31}}.</ref>. L'utilisation de ces propriétés permet d'améliorer les primitives cryptographiques existantes, par exemple en réduisant la taille des [[Clé de chiffrement|clés cryptographiques]], ou de construire de nouvelles primitives cryptographiques qui n'étaient pas connues auparavant<ref>{{Ouvrage|langue=Anglais|auteur1=Henri Cohen, Gerhard Frey, Roberto Avanzi, Christophe Doche, Tanja Lange, Kim Nguyen et Frederik Vercauteren|prénom1=|nom1=|prénom2=|nom2=|prénom3=|nom3=|titre=Handbook of elliptic and hyperelliptic curve cryptography|passage=|lieu=|éditeur=Chapman & Hall/CRC|date=2006|pages totales=|isbn=9781584885184|oclc=58546549|lire en ligne=https://www.worldcat.org/oclc/58546549}}</ref>. |
|||
En 2005, la [[National Security Agency|NSA]] a officiellement annoncé la Suite B de ses recommandations cryptographiques, qui utilise exclusivement la cryptographie sur les courbes elliptiques pour l'[[échange de clé]] et les [[Signature numérique|signatures numériques]]. |
|||
Les [[clé de chiffrement|clés]] employées pour un chiffrement par courbe elliptique sont plus courtes qu'avec un système fondé sur le problème de la factorisation comme [[Rivest Shamir Adleman|RSA]]<ref>{{Lien web|lang=en|url=https://www.keylength.com/|titre=Criptographic Key Length Recommendation|site=BlueKrypt}}.</ref>. Un autre attrait de la cryptographie sur les courbes elliptiques est qu'un [[opérateur bilinéaire]] peut être défini entre les groupes. Cet opérateur se construit à l'aide du [[couplage de Weil]] ou du [[couplage de Tate]]. Les opérateurs bilinéaires se sont récemment vus appliqués de nombreuses façons en cryptographie, par exemple pour le [[schéma basé sur l'identité|chiffrement basé sur l'identité]]. Un point négatif est que les opérations de [[chiffrement]] et de [[déchiffrement]] peuvent avoir une plus grande [[Théorie de la complexité (informatique théorique)|complexité]] que pour d'autres méthodes. |
|||
== Histoire et motivation == |
|||
La résistance d'un système fondé sur les courbes elliptiques repose sur le problème du [[logarithme discret]] dans le [[groupe (mathématiques)|groupe]] correspondant à la courbe elliptique. {{Référence nécessaire|Les développements théoriques sur les courbes étant relativement récents, la cryptographie sur courbe elliptique n'est pas très connue et souffre d'un grand nombre de brevets qui empêchent son développement.}} |
|||
== |
=== Koblitz et Miller === |
||
{{Article détaillé|Courbe elliptique|}} |
|||
Dans le groupe associé à une courbe elliptique, le problème du logarithme discret est considéré comme difficile. On peut donc naturellement y définir l'[[échange de clés Diffie-Hellman basé sur les courbes elliptiques]]. |
|||
La motivation initiale pour l'introduction des courbes elliptiques est qu'il existe des algorithmes sous-exponentiels pour résoudre le problème du [[logarithme discret]] sur les [[corps de nombres]], en particulier le [[Crible algébrique|crible généralisé du corps de nombre]]. Or c'est sur la difficulté du logarithme discret que s'appuient une partie des primitives cryptographiques utilisées pour l'[[échange de clé]] ou la [[Signature numérique|signature]]. Pour assurer un [[niveau de sécurité]] suffisant, il faut donc travailler dans des corps de nombres assez large, ce qui implique un coût d'implémentation, de transmission, et un temps de calcul augmentés d'autant. |
|||
[[Alice et Bob]] se mettent d'accord (publiquement) sur une courbe elliptique <math>E(a,b,p)</math>, c'est-à-dire qu'ils choisissent une [[courbe elliptique]] <math>y^2 = x^3+ax+b\mod p</math>. Ils se mettent aussi d'accord (toujours publiquement) sur un point <math>P</math> situé sur la courbe. |
|||
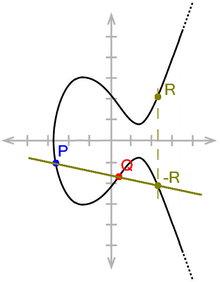
En 1985, Koblitz et Miller remarquent que de tels algorithmes ne sont pas connus pour résoudre le logarithme discret dans le groupe des points rationnels d'une [[courbe elliptique]] est une [[variété algébrique]], c'est-à-dire une collection de points satisfaisant une équation du type <math>y^2 = ax^3 + bx + c</math> avec <math>x, y</math> appartenant à un [[corps fini]]. De manière remarquable, les solutions de cette équation peuvent être dotées d'une [[Groupe (mathématiques)|loi de groupe]]. Complétées d'un fictif « point à l'infini », qui joue le rôle de l'[[élément neutre]], ces solutions forment un [[groupe abélien]] fini. Qui plus est, ces opérations possèdent une interprétation géométrique. On peut donc calculer des « additions » de points sur la courbe. |
|||
On définit <math> n P = P + P + \ldots P </math> (n fois) où l'opération + correspond à la somme de 2 points définie par le symétrique du troisième point d'intersection de la droite définie par les 2 points originaux avec la courbe elliptique. Dans le cas où les deux points à ajouter sont identiques, on considère que la droite qui les joint est la tangente à la courbe elliptique passant par l'un d'entre eux. Un tel point est ''rationnel''. |
|||
Si le groupe est d'ordre premier, il est [[Groupe cyclique|cyclique]], c'est-à-dire qu'il existe un point <math>P = (x, y)</math> qui engendre le groupe par additions successives. Cela est tout à fait analogue à la situation dans les corps finis, où un élément <math>g</math> engendre le sous-groupe <math>\langle g \rangle = \{1, g^2, \dotsc, g^{k}\}</math>. Ainsi, toutes les constructions qui s'appuient sur un groupe du type <math>\langle g \rangle</math> peuvent immédiatement utiliser à la place le groupe <math>E</math> des points rationnels d'une courbe elliptique. |
|||
Secrètement, Alice choisit un entier <math>d_A</math>, et Bob un entier <math>d_B</math>. Alice envoie à Bob le point <math>d_A P</math>, et Bob envoie à Alice <math>d_B P</math>. Chacun de leur côté, ils sont capables de calculer <math>d_A(d_B P) = d_B(d_A P) = d_A d_B P</math> qui est un point de la courbe, et constitue leur clef secrète commune. |
|||
Par exemple, l'[[échange de clé]] de [[Échange de clés Diffie-Hellman|Diffie-Hellman]] se transporte directement en [[Échange de clés Diffie-Hellman basé sur les courbes elliptiques|un algorithme sur courbes elliptiques]]. |
|||
Si Eve a espionné leurs échanges, elle connaît <math>E(a,b,p), P, d_A P, d_B P</math>. Pour pouvoir calculer <math>d_A d_B P</math>, il faut pouvoir calculer <math>d_A</math> connaissant <math>P</math> et <math>d_A P</math>. C'est ce que l'on appelle résoudre le [[logarithme discret]] sur une courbe elliptique. Or, actuellement, si les nombres sont suffisamment grands, on ne connaît pas de méthode efficace pour résoudre ce problème en un temps raisonnable. |
|||
Au moment de leur introduction en cryptographie par Koblitz et Miller, seuls les algorithmes génériques, comme l'[[Baby-step giant-step|algorithme de Shanks]], pouvaient résoudre le logarithme discret dans le groupe de points d'une courbe elliptique. Cela rendait l'attaque beaucoup plus difficile sur une courbe elliptique que sur un corps de nombre. En conséquence, il était possible de conserver un niveau de sécurité satisfaisant, tout en diminuant la taille des données manipulées, d'où un gain de vitesse, une réduction des coûts d'implémentation et de transmission. |
|||
== Implémentation == |
|||
=== |
=== Plongements et attaque MOV === |
||
Il est toutefois apparu rapidement que certaines courbes elliptiques ne sont pas appropriées à cet usage. C'est notamment le cas des courbes supersingulières, pour lesquelles il est possible de ramener le problème du logarithme discret dans un corps fini (où on peut utiliser un algorithme plus efficace pour attaquer). D'une manière générale, toute courbe elliptique sur <math>\mathbb F_q</math> possède un degré de plongement <math>k</math>, tel que le problème du logarithme discret sur la courbe se plonge dans un problème du logarithme discret sur <math>\mathbb F_q^k</math>. Ce plongement est donné par l'[[accouplement de Weil]], un élémént efficacement calculable <math>e(P,Q)</math> qui satisfait notamment <math>e(P,nQ) = e(P,Q)^n = e(nP, Q)</math>. C'est le principe de l'attaque MOV, décrite en 1993 par Menezes, Okamoto et Vanstone<ref>{{Article|langue=Anglais|auteur1=|prénom1=A. J.|nom1=Menezes|prénom2=T.|nom2=Okamoto|prénom3=S. A.|nom3=Vanstone|titre=Reducing elliptic curve logarithms to logarithms in a finite field|périodique=IEEE Transactions on Information Theory|volume=39|numéro=5|date=September 1993|issn=0018-9448|doi=10.1109/18.259647|lire en ligne=http://ieeexplore.ieee.org/document/259647/|consulté le=2018-03-19|pages=1639–1646}}</ref>. |
|||
{{article détaillé|Algorithme de Schoof}} |
|||
D'autres accouplements ont été employés pour monter des attaques similaires, notamment l'[[accouplement de Tate]] et ses variantes (Ate, Eta etc.)<ref>{{Article|langue=en|prénom1=Dan|nom1=Boneh|titre=Pairing-Based Cryptography: Past, Present, and Future|périodique=Advances in Cryptology – ASIACRYPT 2012|série=Lecture Notes in Computer Science|éditeur=Springer, Berlin, Heidelberg|date=2012-12-02|isbn=9783642349607|doi=10.1007/978-3-642-34961-4_1|lire en ligne=https://link.springer.com/chapter/10.1007/978-3-642-34961-4_1|consulté le=2018-03-19|pages=1–1}}</ref>. |
|||
=== Longueur des clés === |
|||
La contre-mesure consiste à choisir, ou construire lorsque c'est possible, des courbes ayant un degré de plongement assez élevé. |
|||
{{refnec|Pour une sécurité de 128 bits, on utilise une courbe sur le corps <math>\mathbb{F}_q</math>, où <math>q \approx 2^{256}</math>}}. |
|||
=== Cryptographie à base de couplages === |
|||
{{Article détaillé|Cryptographie à base de couplages|}} |
|||
En 2002, [[Antoine Joux|Joux]] montre comment utiliser l'accouplement de Weil pour effectuer un [[échange de clé]] tripartite efficace. C'est le point de départ de la cryptographie à base de couplages, qui offre une manière nouvelle de construire des primitives cryptographiques, sous une hypothèse différente que celle de la difficulté du calcul du logarithme discret, et permet de concevoir des primitives pour lesquelles aucune autre implémentation n'est connue. Un autre intérêt de cette approche est la réalisation de schémas de signature numérique courts, comme le [[Signature de Boneh-Lynn-Shacham|schéma de Boneh-Lynn-Shacham]] en 2004<ref>{{Article|langue=en|prénom1=Dan|nom1=Boneh|prénom2=Ben|nom2=Lynn|prénom3=Hovav|nom3=Shacham|titre=Short Signatures from the Weil Pairing|périodique=Journal of Cryptology|volume=17|numéro=4|date=2004-09-01|issn=0933-2790|issn2=1432-1378|doi=10.1007/s00145-004-0314-9|lire en ligne=https://link.springer.com/article/10.1007/s00145-004-0314-9|consulté le=2018-03-19|pages=297–319}}</ref>. |
|||
=== Endomorphismes efficaces : GLV et GLS === |
|||
Sur certaines courbes, il existe en sus de l'opération d'addition entre points un [[endomorphisme]] <math>\phi : E \to E</math> tel que <math>\phi(P) = \lambda P</math> pour un certain <math>\lambda</math>. Si <math>\phi</math> est efficacement calculable, par exemple une opération arithmétique simple sur les coordonnées, alors il permet un « raccourci » : au lieu de calculer <math>\lambda P = P + P + \cdots + P</math> par une succession d'additions, on l'obtient en un seul coup par application de <math>\phi</math>. En fait, il est possible d'accélérer le calcul d'un multiple arbitraire <math>nP</math> en décomposant <math>n = n_1 + \lambda n_2</math> et en calculant <math>nP = n_1 P + n_2 \phi(P)</math> de sorte à répartir l'effort de calcul entre les deux parties. C'est l'idée de la méthode GLV dûe à Gallant, Lambert et Vanstone en 2001<ref>{{Article|langue=en|prénom1=Robert P.|nom1=Gallant|prénom2=Robert J.|nom2=Lambert|prénom3=Scott A.|nom3=Vanstone|titre=Faster Point Multiplication on Elliptic Curves with Efficient Endomorphisms|périodique=Advances in Cryptology — CRYPTO 2001|série=Lecture Notes in Computer Science|éditeur=Springer, Berlin, Heidelberg|date=2001-08-19|isbn=3540446478|doi=10.1007/3-540-44647-8_11|lire en ligne=https://link.springer.com/chapter/10.1007/3-540-44647-8_11|consulté le=2018-03-19|pages=190–200}}</ref>. En 2009, Galbraith, Lin et Scott décrivent une manière de construire des courbes ayant des endomorphismes efficaces, dites courbes GLS<ref>{{Article|langue=en|prénom1=Steven D.|nom1=Galbraith|prénom2=Xibin|nom2=Lin|prénom3=Michael|nom3=Scott|titre=Endomorphisms for Faster Elliptic Curve Cryptography on a Large Class of Curves|périodique=Advances in Cryptology - EUROCRYPT 2009|série=Lecture Notes in Computer Science|éditeur=Springer, Berlin, Heidelberg|date=2009-04-26|isbn=9783642010002|doi=10.1007/978-3-642-01001-9_30|lire en ligne=https://link.springer.com/chapter/10.1007/978-3-642-01001-9_30|consulté le=2018-03-19|pages=518–535}}</ref>. |
|||
=== Cryptographie à base d'isogénies === |
|||
Une [[isogénie]] est un [[morphisme de groupes]] entre les points de deux courbes elliptiques, qui préserve l'élément neutre. Les isogénies des courbes elliptiques possèdent une riche structure, appelée le [[volcan d'isogénies]]. Pour les courbes supersingulières, cette structure est un [[graphe de Ramanujan]] et il devient possible de construire des protocoles cryptographiques reposant sur les propriétés de ce graphe. Un des intérêts de ce point de vue c'est qu'il est complètement indépendant de la question du logarithme discret. Ainsi la cryptographie à base d'isogénies constitue l'une des pistes de recherche en [[cryptographie post-quantique]]. |
|||
=== Cryptographie sur courbes hyperelliptiques === |
|||
{{Article détaillé|Cryptographie sur les courbes hyperelliptiques|}} |
|||
Pour des raisons d'efficacité, il est possible de travailler sur des variétés abéliennes de genre plus grand (généralement de genre 2). Il existe sur les courbes de genre trop grand des méthodes d'indice qui permettent de résoudre le logarithme discret efficacement, ce qui diminue l'intérêt de telles courbes. La théorie des courbes hyperelliptique est moins bien comprise toutefois que celle des courbes elliptiques. |
|||
=== Courbes de Montgomery === |
|||
Une particularité de l'expression <math>y^2 = ax^3 + bx + c</math> est qu'il existe en général, pour une valeur de <math>x</math> donnée, deux valeurs de <math>y</math> possibles, symétriques par rapport à l'axe des abscisses. Ainsi en principe, il est possible de calculer sur une courbe elliptique uniquement à partir de la coordonnée <math>x</math>, si on ne se préoccupe pas du signe de <math>y</math>. Cette idée est rendue concrète par l'utilisation de courbes de Montgomery (aussi appelées surfaces de Kummer, surtout pour les courbes de genre plus grand) qui sont définies comme le quotient de la courbe par l'involution <math>y \mapsto -y</math>. L'intérêt de ne travailler qu'avec une coordonnée est une réduction de la quantité de données manipulées ou transmises, et pour des courbes bien choisies, une réduction du nombre d'opérations effectuées. |
|||
=== Courbes d'Edwards === |
|||
{{Article détaillé|Courbe d'Edwards|}} |
|||
Le calcul d'un multiple <math>nP = P + P + \cdots + P</math> se fait généralement par [[Exponentiation rapide|addition et doublement]]. En général, il y a donc une différence entre l'opération d'addition et de doublement ; et une différence supplémentaire, dans chaque cas, entre une opération impliquant le point à l'infini et une opération ne l'impliquant pas. Ainsi celui qui veut implémenter de tels algorithmes doit être prudent, sans quoi il s'expose potentiellement à une [[Attaque par canal auxiliaire|attaque par canaux auxiliaires]]. Sur les [[Courbe d'Edwards|courbes d'Edwards]], découvertes par Harold Edwards en 2007<ref>{{Article|langue=en-US|prénom1=Harold|nom1=Edwards|titre=A normal form for elliptic curves|périodique=Bulletin of the American Mathematical Society|volume=44|numéro=3|date=2007|issn=0273-0979|issn2=1088-9485|doi=10.1090/s0273-0979-07-01153-6|lire en ligne=http://www.ams.org/home/page/|consulté le=2018-03-19|pages=393–422}}</ref> et introduites en cryptographie par Bernstein et Lange<ref>{{Article|langue=en|prénom1=Daniel J.|nom1=Bernstein|prénom2=Tanja|nom2=Lange|titre=Faster Addition and Doubling on Elliptic Curves|périodique=Advances in Cryptology – ASIACRYPT 2007|série=Lecture Notes in Computer Science|éditeur=Springer, Berlin, Heidelberg|date=2007-12-02|isbn=9783540768999|doi=10.1007/978-3-540-76900-2_3|lire en ligne=https://link.springer.com/chapter/10.1007/978-3-540-76900-2_3|consulté le=2018-03-19|pages=29–50}}</ref>, il est possible d'utiliser une même opération pour addition, doublement, avec ou sans points à l'infini, ce qui élimine structurellement ces canaux auxiliaires et facilite l'implémentation. |
|||
=== Attaque en point initial et twists === |
|||
Dans certains cas, par exemple sur une courbe de Montgomery, ou lors d'une [[Attaque par faute|attaque par fautes]], il est possible qu'un utilisateur manipule sans le savoir un point qui n'appartient pas à la courbe elliptique. S'il applique néanmoins les opérations d'addition et de doublement, et révèle le résultat, il peut en fait renseigner l'adversaire sur des données secrètes. C'est notamment le cas lors d'une opération de signature, où le signataire calcule un point de la forme <math>P \mapsto k P</math> avec <math>k</math> secret. Dans des conditions normales, retrouver <math>k</math> nécessite de résoudre un problème de logarithme discret, qui est difficile sur la courbe utilisée pour la signature ; mais si l'adversaire parvient à manipuler <math>P</math> alors <math>kP</math> peut appartenir à une courbe beaucoup plus faible, sur laquelle l'adversaire sait calculer le logarithme discret. |
|||
Dans le cas d'une courbe de Montgomery, l'adversaire peut aisément modifier un unique bit de la coordonnée <math>x</math>, ce qui force sa cible à travailler sur un twist quadratique de la courbe elliptique, c'est-à-dire une courbe d'équation <math>dy^2 = ax^3 + bx + c</math> où <math>d</math> n'est pas un [[résidu quadratique]]. Si une courbe n'est pas choisie avec précaution, il est possible d'attaquer au moyen de ses twists. |
|||
=== Factorisation par courbes elliptiques === |
|||
{{Article détaillé|Factorisation de Lenstra par les courbes elliptiques|}} |
|||
La factorisation de [[Hendrik Lenstra|Lenstra]] par les courbes elliptiques est un [[algorithme probabiliste]] rapide pour la [[décomposition en produit de facteurs premiers]] qui emploie les [[Courbe elliptique|courbes elliptiques]]. |
|||
== Courbes utilisées en cryptographie == |
|||
* [[Curve25519]], d'équation <var>y</var><sup>2</sup> = <var>x</var><sup>3</sup> + 486662<var>x</var><sup>2</sup> + <var>x,</var> une courbe de Montgomery conçue pour l'[[Échange de clés Diffie-Hellman basé sur les courbes elliptiques|échange de clé de Diffie-Hellman]]. |
|||
* Ed25519, twist quadratique de la précédente, une courbe d'Edwards conçue pour la signature numérique [[ECDSA]] ou [[EdDSA]]. |
|||
* NIST P-256, définie par la NSA dans sa Suite B. |
|||
* secp256k1, utilisée pour les signatures [[Bitcoin]], une courbe GLV. |
|||
* Familles Barreto-Naehrig, Miyaji-Nakabayashi-Takano, Brezing-Weng, Kachisa-Shaefer-Scott pour la cryptographie à base de couplages<ref>{{Article|langue=en|prénom1=David|nom1=Freeman|prénom2=Michael|nom2=Scott|prénom3=Edlyn|nom3=Teske|titre=A Taxonomy of Pairing-Friendly Elliptic Curves|périodique=Journal of Cryptology|volume=23|numéro=2|date=2010-04-01|issn=0933-2790|issn2=1432-1378|doi=10.1007/s00145-009-9048-z|lire en ligne=https://link.springer.com/article/10.1007/s00145-009-9048-z|consulté le=2018-03-19|pages=224–280}}</ref>. |
|||
* Courbes supersingulières, utilisées pour la cryptographie à base d'isogénies. |
|||
== Notes et références == |
== Notes et références == |
||
{{Ars Cryptographica}} |
|||
{{Références|taille=36}} |
{{Références|taille=36}} |
||
Version du 19 mars 2018 à 19:58
La cryptographie sur les courbes elliptiques regroupe un ensemble de techniques cryptographiques qui utilisent une ou plusieurs propriétés des courbes elliptiques, ou plus généralement d'une variété abélienne. L'usage des courbes elliptiques en cryptographie a été suggéré, de manière indépendante, par Neal Koblitz et Victor Miller en 1985[1],[2]. L'utilisation de ces propriétés permet d'améliorer les primitives cryptographiques existantes, par exemple en réduisant la taille des clés cryptographiques, ou de construire de nouvelles primitives cryptographiques qui n'étaient pas connues auparavant[3].
En 2005, la NSA a officiellement annoncé la Suite B de ses recommandations cryptographiques, qui utilise exclusivement la cryptographie sur les courbes elliptiques pour l'échange de clé et les signatures numériques.
Histoire et motivation
Koblitz et Miller
La motivation initiale pour l'introduction des courbes elliptiques est qu'il existe des algorithmes sous-exponentiels pour résoudre le problème du logarithme discret sur les corps de nombres, en particulier le crible généralisé du corps de nombre. Or c'est sur la difficulté du logarithme discret que s'appuient une partie des primitives cryptographiques utilisées pour l'échange de clé ou la signature. Pour assurer un niveau de sécurité suffisant, il faut donc travailler dans des corps de nombres assez large, ce qui implique un coût d'implémentation, de transmission, et un temps de calcul augmentés d'autant.
En 1985, Koblitz et Miller remarquent que de tels algorithmes ne sont pas connus pour résoudre le logarithme discret dans le groupe des points rationnels d'une courbe elliptique est une variété algébrique, c'est-à-dire une collection de points satisfaisant une équation du type avec appartenant à un corps fini. De manière remarquable, les solutions de cette équation peuvent être dotées d'une loi de groupe. Complétées d'un fictif « point à l'infini », qui joue le rôle de l'élément neutre, ces solutions forment un groupe abélien fini. Qui plus est, ces opérations possèdent une interprétation géométrique. On peut donc calculer des « additions » de points sur la courbe.
Si le groupe est d'ordre premier, il est cyclique, c'est-à-dire qu'il existe un point qui engendre le groupe par additions successives. Cela est tout à fait analogue à la situation dans les corps finis, où un élément engendre le sous-groupe . Ainsi, toutes les constructions qui s'appuient sur un groupe du type peuvent immédiatement utiliser à la place le groupe des points rationnels d'une courbe elliptique.
Par exemple, l'échange de clé de Diffie-Hellman se transporte directement en un algorithme sur courbes elliptiques.
Au moment de leur introduction en cryptographie par Koblitz et Miller, seuls les algorithmes génériques, comme l'algorithme de Shanks, pouvaient résoudre le logarithme discret dans le groupe de points d'une courbe elliptique. Cela rendait l'attaque beaucoup plus difficile sur une courbe elliptique que sur un corps de nombre. En conséquence, il était possible de conserver un niveau de sécurité satisfaisant, tout en diminuant la taille des données manipulées, d'où un gain de vitesse, une réduction des coûts d'implémentation et de transmission.
Plongements et attaque MOV
Il est toutefois apparu rapidement que certaines courbes elliptiques ne sont pas appropriées à cet usage. C'est notamment le cas des courbes supersingulières, pour lesquelles il est possible de ramener le problème du logarithme discret dans un corps fini (où on peut utiliser un algorithme plus efficace pour attaquer). D'une manière générale, toute courbe elliptique sur possède un degré de plongement , tel que le problème du logarithme discret sur la courbe se plonge dans un problème du logarithme discret sur . Ce plongement est donné par l'accouplement de Weil, un élémént efficacement calculable qui satisfait notamment . C'est le principe de l'attaque MOV, décrite en 1993 par Menezes, Okamoto et Vanstone[4].
D'autres accouplements ont été employés pour monter des attaques similaires, notamment l'accouplement de Tate et ses variantes (Ate, Eta etc.)[5].
La contre-mesure consiste à choisir, ou construire lorsque c'est possible, des courbes ayant un degré de plongement assez élevé.
Cryptographie à base de couplages
En 2002, Joux montre comment utiliser l'accouplement de Weil pour effectuer un échange de clé tripartite efficace. C'est le point de départ de la cryptographie à base de couplages, qui offre une manière nouvelle de construire des primitives cryptographiques, sous une hypothèse différente que celle de la difficulté du calcul du logarithme discret, et permet de concevoir des primitives pour lesquelles aucune autre implémentation n'est connue. Un autre intérêt de cette approche est la réalisation de schémas de signature numérique courts, comme le schéma de Boneh-Lynn-Shacham en 2004[6].
Endomorphismes efficaces : GLV et GLS
Sur certaines courbes, il existe en sus de l'opération d'addition entre points un endomorphisme tel que pour un certain . Si est efficacement calculable, par exemple une opération arithmétique simple sur les coordonnées, alors il permet un « raccourci » : au lieu de calculer par une succession d'additions, on l'obtient en un seul coup par application de . En fait, il est possible d'accélérer le calcul d'un multiple arbitraire en décomposant et en calculant de sorte à répartir l'effort de calcul entre les deux parties. C'est l'idée de la méthode GLV dûe à Gallant, Lambert et Vanstone en 2001[7]. En 2009, Galbraith, Lin et Scott décrivent une manière de construire des courbes ayant des endomorphismes efficaces, dites courbes GLS[8].
Cryptographie à base d'isogénies
Une isogénie est un morphisme de groupes entre les points de deux courbes elliptiques, qui préserve l'élément neutre. Les isogénies des courbes elliptiques possèdent une riche structure, appelée le volcan d'isogénies. Pour les courbes supersingulières, cette structure est un graphe de Ramanujan et il devient possible de construire des protocoles cryptographiques reposant sur les propriétés de ce graphe. Un des intérêts de ce point de vue c'est qu'il est complètement indépendant de la question du logarithme discret. Ainsi la cryptographie à base d'isogénies constitue l'une des pistes de recherche en cryptographie post-quantique.
Cryptographie sur courbes hyperelliptiques
Pour des raisons d'efficacité, il est possible de travailler sur des variétés abéliennes de genre plus grand (généralement de genre 2). Il existe sur les courbes de genre trop grand des méthodes d'indice qui permettent de résoudre le logarithme discret efficacement, ce qui diminue l'intérêt de telles courbes. La théorie des courbes hyperelliptique est moins bien comprise toutefois que celle des courbes elliptiques.
Courbes de Montgomery
Une particularité de l'expression est qu'il existe en général, pour une valeur de donnée, deux valeurs de possibles, symétriques par rapport à l'axe des abscisses. Ainsi en principe, il est possible de calculer sur une courbe elliptique uniquement à partir de la coordonnée , si on ne se préoccupe pas du signe de . Cette idée est rendue concrète par l'utilisation de courbes de Montgomery (aussi appelées surfaces de Kummer, surtout pour les courbes de genre plus grand) qui sont définies comme le quotient de la courbe par l'involution . L'intérêt de ne travailler qu'avec une coordonnée est une réduction de la quantité de données manipulées ou transmises, et pour des courbes bien choisies, une réduction du nombre d'opérations effectuées.
Courbes d'Edwards
Le calcul d'un multiple se fait généralement par addition et doublement. En général, il y a donc une différence entre l'opération d'addition et de doublement ; et une différence supplémentaire, dans chaque cas, entre une opération impliquant le point à l'infini et une opération ne l'impliquant pas. Ainsi celui qui veut implémenter de tels algorithmes doit être prudent, sans quoi il s'expose potentiellement à une attaque par canaux auxiliaires. Sur les courbes d'Edwards, découvertes par Harold Edwards en 2007[9] et introduites en cryptographie par Bernstein et Lange[10], il est possible d'utiliser une même opération pour addition, doublement, avec ou sans points à l'infini, ce qui élimine structurellement ces canaux auxiliaires et facilite l'implémentation.
Attaque en point initial et twists
Dans certains cas, par exemple sur une courbe de Montgomery, ou lors d'une attaque par fautes, il est possible qu'un utilisateur manipule sans le savoir un point qui n'appartient pas à la courbe elliptique. S'il applique néanmoins les opérations d'addition et de doublement, et révèle le résultat, il peut en fait renseigner l'adversaire sur des données secrètes. C'est notamment le cas lors d'une opération de signature, où le signataire calcule un point de la forme avec secret. Dans des conditions normales, retrouver nécessite de résoudre un problème de logarithme discret, qui est difficile sur la courbe utilisée pour la signature ; mais si l'adversaire parvient à manipuler alors peut appartenir à une courbe beaucoup plus faible, sur laquelle l'adversaire sait calculer le logarithme discret.
Dans le cas d'une courbe de Montgomery, l'adversaire peut aisément modifier un unique bit de la coordonnée , ce qui force sa cible à travailler sur un twist quadratique de la courbe elliptique, c'est-à-dire une courbe d'équation où n'est pas un résidu quadratique. Si une courbe n'est pas choisie avec précaution, il est possible d'attaquer au moyen de ses twists.
Factorisation par courbes elliptiques
La factorisation de Lenstra par les courbes elliptiques est un algorithme probabiliste rapide pour la décomposition en produit de facteurs premiers qui emploie les courbes elliptiques.
Courbes utilisées en cryptographie
- Curve25519, d'équation y2 = x3 + 486662x2 + x, une courbe de Montgomery conçue pour l'échange de clé de Diffie-Hellman.
- Ed25519, twist quadratique de la précédente, une courbe d'Edwards conçue pour la signature numérique ECDSA ou EdDSA.
- NIST P-256, définie par la NSA dans sa Suite B.
- secp256k1, utilisée pour les signatures Bitcoin, une courbe GLV.
- Familles Barreto-Naehrig, Miyaji-Nakabayashi-Takano, Brezing-Weng, Kachisa-Shaefer-Scott pour la cryptographie à base de couplages[11].
- Courbes supersingulières, utilisées pour la cryptographie à base d'isogénies.
Notes et références
- (en) Neal Koblitz, « Elliptic curve cryptosystems », Mathematics of Computation, no 48, , p. 203-209 (DOI 10.1090/S0025-5718-1987-0866109-5).
- (en) Victor S. Miller, « Use of elliptic curves in cryptography », Crypto, vol. 218, , p. 417-426 (DOI 10.1007/3-540-39799-X_31).
- (en) Henri Cohen, Gerhard Frey, Roberto Avanzi, Christophe Doche, Tanja Lange, Kim Nguyen et Frederik Vercauteren, Handbook of elliptic and hyperelliptic curve cryptography, Chapman & Hall/CRC, (ISBN 9781584885184, OCLC 58546549, lire en ligne)
- (en) A. J. Menezes, T. Okamoto et S. A. Vanstone, « Reducing elliptic curve logarithms to logarithms in a finite field », IEEE Transactions on Information Theory, vol. 39, no 5, , p. 1639–1646 (ISSN 0018-9448, DOI 10.1109/18.259647, lire en ligne, consulté le )
- (en) Dan Boneh, « Pairing-Based Cryptography: Past, Present, and Future », Advances in Cryptology – ASIACRYPT 2012, Springer, Berlin, Heidelberg, lecture Notes in Computer Science, , p. 1–1 (ISBN 9783642349607, DOI 10.1007/978-3-642-34961-4_1, lire en ligne, consulté le )
- (en) Dan Boneh, Ben Lynn et Hovav Shacham, « Short Signatures from the Weil Pairing », Journal of Cryptology, vol. 17, no 4, , p. 297–319 (ISSN 0933-2790 et 1432-1378, DOI 10.1007/s00145-004-0314-9, lire en ligne, consulté le )
- (en) Robert P. Gallant, Robert J. Lambert et Scott A. Vanstone, « Faster Point Multiplication on Elliptic Curves with Efficient Endomorphisms », Advances in Cryptology — CRYPTO 2001, Springer, Berlin, Heidelberg, lecture Notes in Computer Science, , p. 190–200 (ISBN 3540446478, DOI 10.1007/3-540-44647-8_11, lire en ligne, consulté le )
- (en) Steven D. Galbraith, Xibin Lin et Michael Scott, « Endomorphisms for Faster Elliptic Curve Cryptography on a Large Class of Curves », Advances in Cryptology - EUROCRYPT 2009, Springer, Berlin, Heidelberg, lecture Notes in Computer Science, , p. 518–535 (ISBN 9783642010002, DOI 10.1007/978-3-642-01001-9_30, lire en ligne, consulté le )
- (en-US) Harold Edwards, « A normal form for elliptic curves », Bulletin of the American Mathematical Society, vol. 44, no 3, , p. 393–422 (ISSN 0273-0979 et 1088-9485, DOI 10.1090/s0273-0979-07-01153-6, lire en ligne, consulté le )
- (en) Daniel J. Bernstein et Tanja Lange, « Faster Addition and Doubling on Elliptic Curves », Advances in Cryptology – ASIACRYPT 2007, Springer, Berlin, Heidelberg, lecture Notes in Computer Science, , p. 29–50 (ISBN 9783540768999, DOI 10.1007/978-3-540-76900-2_3, lire en ligne, consulté le )
- (en) David Freeman, Michael Scott et Edlyn Teske, « A Taxonomy of Pairing-Friendly Elliptic Curves », Journal of Cryptology, vol. 23, no 2, , p. 224–280 (ISSN 0933-2790 et 1432-1378, DOI 10.1007/s00145-009-9048-z, lire en ligne, consulté le )
Voir aussi
Bibliographie
- (en) Ian F. Blake, Gadiel Seroussi et Nigel P. Smart, Elliptic Curves in Cryptography, Cambridge University Press, (ISBN 9780521653749)
- (en) Darrel Hankerson, Alfred J. Menezes et Scott Vanstone, Guide to Elliptic Curve Cryptography, Springer-Verlag, (ISBN 9780387218465)
- (en) Lawrence C. Washington, Elliptic Curves: Number Theory and Cryptography, Chapman & Hall/CRC, (ISBN 9781420071474)
Articles connexes
Liens externes
- « Chiffrer avec des courbes elliptiques », sur bibmath.net
- (en) ECC a gentle introduction





























