Triangulation de Delaunay

En mathématiques et plus particulièrement en géométrie algorithmique, la triangulation de Delaunay d'un ensemble $P$ de points du plan est une triangulation $DT(P)$ telle qu'aucun point de $P$ n'est à l'intérieur du cercle circonscrit d'un des triangles de $DT(P)$ . Les triangulations de Delaunay maximisent le plus petit angle de l'ensemble des angles des triangles, évitant ainsi les triangles « allongés ». Cette triangulation a été inventée par le mathématicien russe Boris Delaunay, dans un article publié en 1924^[1].

D'après la définition de Delaunay^[1], le cercle circonscrit d'un triangle constitué de trois points de l'ensemble de départ est vide s'il ne contient pas d'autres sommets que les siens. Ainsi, les autres points sont autorisés sur le périmètre en lui-même mais pas à l'intérieur strict du cercle circonscrit.

La condition de Delaunay affirme qu'un réseau de triangles est une triangulation de Delaunay si tous les cercles circonscrits des triangles du réseau sont vides. Ceci constitue la définition originale en deux dimensions. En remplaçant les cercles par des sphères circonscrites, il est possible d'étendre la définition à la dimension trois.

Il n'existe pas de triangulation de Delaunay pour un ensemble de points alignés. De toute manière, la triangulation n'est dans ce cas pas définie.

Pour 4 points cocycliques, tels que les sommets d'un rectangle, la triangulation de Delaunay n'est pas unique. Trivialement, les triangulations utilisant chacune des deux diagonales satisfont la condition de Delaunay.

Il est possible de généraliser cette notion pour des mesures non euclidiennes, sans garantie de l'existence ou de l'unicité de la triangulation.

Relation avec les diagrammes de Voronoï

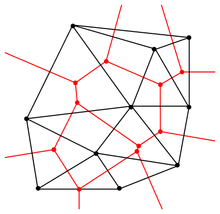
La triangulation de Delaunay d’un ensemble discret $P$ de points est le graphe dual du diagramme de Voronoï associé à $P$ .

Passage de la triangulation de Delaunay au diagramme de Voronoï

Les sommets du diagramme de Voronoï sont les centres des cercles circonscrits des triangles de la triangulation de Delaunay. Les arêtes du diagramme de Voronoï sont sur les médiatrices des arêtes de la triangulation de Delaunay (cependant les arêtes de Voronoï sont des segments ou demi-droites qui n'ont pas nécessairement d'intersection sur le centre de ces médiatrices, comme on peut le voir sur la figure ci-contre).

Passage du diagramme de Voronoï à la triangulation de Delaunay

Chaque germe du diagramme de Voronoï constitue un sommet dans la triangulation de Delaunay. Ces sommets sont reliés entre eux par une arête si et seulement si les cellules sont adjacentes.

DEL(P)=\{(a,b)\in P^{2}\mid Vor_{P}(a)\cap Vor_{P}(b)\neq \varnothing \}

.

En dimension quelconque

Pour un ensemble $P$ de points dans l'espace Euclidien en n dimensions, une triangulation de Delaunay est une triangulation $DT(P)$ telle qu'aucun point de $P$ ne se trouve dans l'hypersphère circonscrite d'un simplexe de $DT(P)$ .

Une triangulation de Delaunay dans le plan est unique si les points sont dans une position généraleposition générale, c'est-à-dire en dimension 2 s'il n'y a pas trois points alignés ou quatre points cocycliques et, en dimension $d$ , il suffit qu'il n'y ait pas $d+1$ points dans le même hyperplan et $d + 2$ sur la même hypersphère.

Le problème de la construction de la triangulation de Delaunay d'un ensemble de points en dimension $n$ dans un espace euclidien peut être ramené au problème de la construction de l'enveloppe convexe d'un ensemble de points en dimension $n + 1$ . Pour ce faire, on attribue à chaque point $p$ une coordonnée supplémentaire, que l'on fixe à $|p|^{2}$ , on prend le fond de l'enveloppe convexe et on retourne en dimension $n$ en supprimant la dernière coordonnée. Comme l'enveloppe convexe est unique, la triangulation l'est aussi tant que toutes les faces de l'enveloppe convexe sont des simplexes. Si une face n'est pas un simplexe, cela signifie que $n + 2$ points se trouvent sur la même hypersphère et donc que les points ne sont pas en position générale.

Propriétés

Soient $n$ le nombre de points et $d$ le nombre de dimensions.

L'union de tous les simplexes d'une triangulation constitue l'enveloppe convexe des points.
La triangulation de Delaunay contient au plus $O(n^{\lceil d/2\rceil })$ simplexes.
Dans le plan, c'est-à-dire pour $d = 2$ , s'il y a $b$ sommets dans l'enveloppe convexe, alors toute triangulation a exactement $2 n - 2 - b$ triangles (voir la caractéristique d'Euler).
Dans le plan, chaque sommet est en moyenne entouré de six triangles.
Si un cercle passant par deux des points de l'ensemble n'en contient aucun autre dans son intérieur, alors le segment reliant les deux points est un segment de la triangulation de cet ensemble.
La triangulation de Delaunay d'un ensemble de points dans un espace de dimension d est la projection de l'enveloppe convexe des projections des points sur une paraboloïde de dimension d + 1.

Une définition visuelle : le basculement

D'après les propriétés précédentes, on peut remarquer qu'avec deux triangles ABD et BCD donnés (voir figure), la somme des angles α et γ est inférieure ou égale à 180° si et seulement si ces triangles respectent la condition de Delaunay.

C'est une propriété importante car elle permet de déterminer une technique de construction. Si deux triangles ABD et CBD ne respectent pas la condition de Delaunay, il faut remplacer l'arête commune BD par l'arête commune AC (ce qui constitue le basculement), pour obtenir deux triangles ABC et ACD qui respectent la condition de Delaunay :

Cette triangulation ne respecte pas la propriété précédente : la somme de α et γ vaut plus que 180°.
La nouvelle triangulation ne vérifie pas la condition de Delaunay : les cercles circonscrits ne sont pas vides.
Le basculement d'arête produit une triangulation de Delaunay.

Algorithmes

Tous les algorithmes de construction d'une triangulation de Delaunay reposent sur des opérations rapides permettant de déterminer la position d'un point par rapport à un cercle circonscrit à un triangle, et de structures de données efficaces pour conserver les triangles et les sommets.

Dans le plan, pour vérifier si un point D se trouve dans le cercle circonscrit à A, B et C, il suffit d'évaluer le déterminant de la matrice suivante :

${\begin{vmatrix}A_{x}&A_{y}&A_{x}^{2}+A_{y}^{2}&1\\B_{x}&B_{y}&B_{x}^{2}+B_{y}^{2}&1\\C_{x}&C_{y}&C_{x}^{2}+C_{y}^{2}&1\\D_{x}&D_{y}&D_{x}^{2}+D_{y}^{2}&1\end{vmatrix}}={\begin{vmatrix}A_{x}-D_{x}&A_{y}-D_{y}&(A_{x}^{2}-D_{x}^{2})+(A_{y}^{2}-D_{y}^{2})\\B_{x}-D_{x}&B_{y}-D_{y}&(B_{x}^{2}-D_{x}^{2})+(B_{y}^{2}-D_{y}^{2})\\C_{x}-D_{x}&C_{y}-D_{y}&(C_{x}^{2}-D_{x}^{2})+(C_{y}^{2}-D_{y}^{2})\\\end{vmatrix}}>0$

Si A, B et C sont placés dans le sens anti-horaire, le déterminant est positif si et seulement si D se trouve dans le cercle circonscrit.

Algorithmes de basculement

Comme mentionné ci-dessus, si un triangle n'est pas de Delaunay, il est possible de basculer l'un de ses côtés. On construit ainsi un algorithme direct : on génère d'abord une triangulation quelconque, puis on bascule les arêtes jusqu'à ce que tous les triangles soient de Delaunay. Cette méthode peut nécessiter $O(n 2)$ basculements d'arêtes et ne peut se généraliser en dimension 3 ou supérieure^[2].

Incrémentation

La manière la plus directe de générer efficacement une triangulation de Delaunay est d'ajouter les sommets un par un en recalculant la triangulation des parties du graphe affectées par cet ajout. Lorsqu'un sommet s est ajouté, le triangle contenant s est séparé en trois puis on leur applique l'algorithme de basculement. Fait de manière naïve, cela se fera en temps O(n) : il faut chercher parmi tous les triangles pour trouver celui qui contient s et tous les triangles vont ensuite potentiellement basculer. Comme il faut faire cela pour chaque sommet, le temps total d'exécution est en $O(n 2)$ .

Si les sommets sont insérés dans un ordre aléatoire, chaque insertion ne va faire basculer, en moyenne, que O(1) triangles, même si parfois beaucoup plus vont basculer^[3].

Pour améliorer la recherche de la position du point, il est possible de stocker l'historique des partitionnements et des basculements effectués : chaque triangle garde en mémoire un pointeur vers les deux ou trois triangles qui l'ont remplacé. Pour trouver le triangle qui contient s, commencer à un triangle racine, puis suivre les pointeurs jusqu'à arriver à un triangle qui n'a pas été remplacé. En moyenne, cela se fera en temps O(log n). Ainsi, pour rechercher le triangle conteneur de chaque sommet, cela se fera en temps O(n log n)^[2]. La technique peut être généralisée à des espaces de dimension quelconque, comme l'ont prouvé Edelsbrunner et Shah^[4], mais la complexité temporelle peut être exponentielle, y compris si la triangulation finale est petite.

Une autre manière, afin d'éviter la recherche de triangles, vise à introduire les points suivant l'ordre lexicographique. On associe le nouveau point à son prédécesseur ensuite on parcourt de part et d'autre l'enveloppe convexe pour former et légaliser les nouveaux triangles qui sont relatifs à ce nouveau point. Cette méthode est limitée car pour introduire un nouveau point qui n'est pas lexicographiquement supérieur aux autres, il faudra tout reconstruire. Elle requiert la connaissance parfaite de l'ensemble de points.

L'algorithme de Bowyer-Watson est une autre approche de construction incrémentale. Il donne une alternative au basculement en supprimant les triangles (ou simplexes) dont les cercles (ou hypersphère) circonscrits contiennent le nouveau point et en re-triangulant la cavité en étoile ainsi formé.

Diviser pour régner

Lee et Schachter ont mis au point un algorithme diviser pour régner appliqué à la triangulation en deux dimensions qui a ensuite été amélioré par Guibas et Stolfi^[5] puis par Dwyer. Dans cet algorithme, une ligne est récursivement dessinée pour séparer les points en deux ensembles. La triangulation de Delaunay est calculée pour chacun des ensembles puis ils sont fusionnés. Avec quelques astuces, la fusion peut se faire en O(n). Ainsi, le temps total de calcul est en O(n log n)^[6].

Applications

L'arbre euclidien couvrant de poids minimum d'un ensemble de points est un sous-ensemble de la triangulation de Delaunay de ces mêmes points. Ce résultat permet de calculer efficacement cet arbre.

Pour modéliser un terrain ou d'autres objets à partir d'un ensemble de points donnés, la triangulation de Delaunay fournit un bon ensemble de triangles qui pourront ensuite être utilisés comme polygones dans le modèle.

Les triangulations de Delaunay sont souvent utilisées pour construire les mailles de la méthode des éléments finis à cause de la garantie sur les angles et grâce à la vitesse des algorithmes. Typiquement, le domaine dont on veut construire les mailles est décrit comme un gros complexe simplicial. Pour que le maillage soit stable numériquement, il faut qu'il soit raffiné, par exemple en utilisant l'algorithme de Ruppert (en). Jonathan Shewchuk a publié une bibliothèque libre sur les triangles^[7].

Les triangulations de Delaunay sont également utilisés en volumes finis, notamment en mécanique des fluides, pour générer des maillages non structurés sur des géométries complexes^[8].

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Delaunay triangulation » (voir la liste des auteurs).

↑ ^{a et b} B. Delaunay, « Sur la sphère vide », Proceedings du Congrès international des mathématiciens de 1924, p. 695-700.
↑ ^{a et b} (en) Mark de Berg, Otfried Cheong, Marc van Kreveld et Mark Overmars, Computational Geometry: Algorithms and Applications, Berlin, Springer-Verlag, 2008, 3^e éd. (ISBN 978-3-540-77973-5, LCCN 2008921564, lire en ligne).
↑ (en) L. Guibas, D. Knuth et M. Sharir (en), « Randomized incremental construction of Delaunay and Voronoi diagrams », Algorithmica, vol. 7,‎ 1992, p. 381-413 (lire en ligne).
↑ (en) Herbert Edelsbrunner (en) et Nimish Shah, « Incremental Topological Flipping Works for Regular Triangulations », Algorithmica, vol. 15,‎ 1996, p. 223-241 (lire en ligne).
↑ Voir référence dans (en) Samuel Peterson, Undergraduate, « Computing Constrained Delaunay Triangulations », sur Université du Minnesota, 1998.
↑ (en) G. Leach, « Improving Worst-Case Optimal Delaunay Triangulation Algorithms », juin 1992.
↑ (en) Triangle.
↑ (en) N. P. Weatherill, « Delaunay triangulation in computational fluid dynamics », Computers & Mathematics with Applications, vol. 24, n^o 5,‎ 1^er septembre 1992, p. 129–150 (ISSN 0898-1221, DOI 10.1016/0898-1221(92)90045-J, lire en ligne, consulté le 4 février 2019)

Voir aussi

Articles connexes

Lien externe

Cours sur la triangulation de Delaunay

[Delaunay1924-1] {a et b} B. Delaunay, « Sur la sphère vide », Proceedings du Congrès international des mathématiciens de 1924, p. 695-700.

[deBerg-2] {a et b} (en) Mark de Berg, Otfried Cheong, Marc van Kreveld et Mark Overmars, Computational Geometry: Algorithms and Applications, Berlin, Springer-Verlag, 2008, 3^e éd. (ISBN 978-3-540-77973-5, LCCN 2008921564, lire en ligne).

[3] (en) L. Guibas, D. Knuth et M. Sharir (en), « Randomized incremental construction of Delaunay and Voronoi diagrams », Algorithmica, vol. 7,‎ 1992, p. 381-413 (lire en ligne).

[4] (en) Herbert Edelsbrunner (en) et Nimish Shah, « Incremental Topological Flipping Works for Regular Triangulations », Algorithmica, vol. 15,‎ 1996, p. 223-241 (lire en ligne).

[5] Voir référence dans (en) Samuel Peterson, Undergraduate, « Computing Constrained Delaunay Triangulations », sur Université du Minnesota, 1998.

[Leach1992-6] (en) G. Leach, « Improving Worst-Case Optimal Delaunay Triangulation Algorithms », juin 1992.

[7] (en) Triangle.

[8] (en) N. P. Weatherill, « Delaunay triangulation in computational fluid dynamics », Computers & Mathematics with Applications, vol. 24, n^o 5,‎ 1^er septembre 1992, p. 129–150 (ISSN 0898-1221, DOI 10.1016/0898-1221(92)90045-J, lire en ligne, consulté le 4 février 2019)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]