Surplus du consommateur
Le surplus du consommateur est la différence entre ce qu'un consommateur est prêt à payer pour un bien et le montant effectivement payé.
Le surplus du consommateur[modifier | modifier le code]
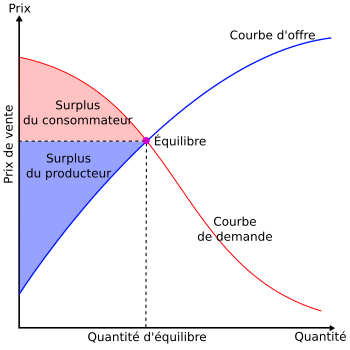
Le surplus du consommateur est un concept élaboré par Dupuit pour le choix des travaux publics à effectuer. Prenons le cas d’un péage pour traverser un pont. Il y a des individus qui seraient prêts à payer davantage que ce prix pour traverser le pont. La différence entre le prix maximum qu’ils seraient prêts à payer et le prix payé représente le surplus du consommateur. Graphiquement, le surplus du consommateur est donné par la surface sous la courbe de demande au-dessus du prix d’équilibre (surface rouge).
Marshall a indiqué que le concept de Dupuit était valable si l’utilité marginale du revenu était constante. En effet, soit la fonction de demande avec p le prix (ou le vecteurs des prix) et y le revenu. Le surplus du consommateur lorsque le prix passe de po (par exemple, le prix maximum) à p1 (par exemple, le prix d’équilibre) est :
Soit l’utilité indirecte v(p,y) (l’utilité maximale du consommateur lorsque les prix sont p et le revenu y : où x sont les quantités consommées). On peut écrire ainsi l’identité de Roy :
où est l’utilité marginale du revenu.
Le surplus du consommateur devient alors :
Si l’utilité marginale est constante, comme Marshall avait supposé, on peut écrire :
Le terme à droite entre parenthèses représente la variation de l’utilité. L’utilité marginale du revenu transforme cette grandeur qui ne peut pas être mesurée en une valeur monétaire (la surface sous la courbe de demande représente des euros ou des $ car c’est le produit d’un prix fois la quantité). On dispose ainsi d’une méthode opérationnelle pour mesurer la variation de l’utilité.
L’hypothèse d’une utilité marginale constante est toutefois très restrictive et peu réaliste. En effet, si les premières unités sont payées au prix maximum, le consommateur aura moins d’argent pour acheter les unités suivantes. L’utilité marginale n’est pas constante. Marshall suppose alors qu’elle est approximativement constante en disant que la dépense pour un bien particulier représente une petite fraction du revenu.
Les variations compensée et équivalente[modifier | modifier le code]
Dans le cas général, on pourrait calculer le « vrai » surplus du consommateur de la manière suivante. Supposons que le prix du lait baisse de po à p1. L’utilité du consommateur augmente. On peut définir le « vrai » surplus comme la somme qu’il faut prendre au consommateur pour que son utilité ne change pas. Cette somme est appelée la variation compensée et elle peut être définie en utilisant la fonction de coût ou de dépense qui est la dépense minimale pour avoir un certain niveau d’utilité :
La variation compensée est alors :
On pourrait aussi prendre le niveau de satisfaction après la baisse du prix. Supposons que le gouvernement désire intervenir pour empêcher cette baisse afin de soutenir le revenu des paysans. Quelle somme faut-il donner au consommateur pour le compenser de cette baisse qui n’a pas eu lieu ? Ce montant est appelé la variation équivalente :
D’après le lemme de Shephard, la dérivée de la fonction de coût par rapport au prix donne la fonction de demande conditionnelle ou demande compensée :
On parle aussi de demande hicksienne, en l’honneur de Hicks. La demande usuelle est alors appelée demande marshallienne car Marshall a beaucoup fait usage de cette fonction. Si l’on prend la surface sous la demande compensée on obtient la variation compensée :
Comme la surface sous la demande hicksienne est souvent plus petite que celle sous la demande marshallienne, le surplus du consommateur surestime la variation de l’utilité. Dans des cas pratiques, on peut toujours effectuer une intégration numérique de la fonction de coût. Par ailleurs, la fonction de coût peut être obtenue en prenant la fonction de demande.
Bibliographie[modifier | modifier le code]
- A.Deaton and J. Muellbauer, Economics and Consumer Behavior, Cambridge, 1980
- J. Dupuit, “De la mesure de l’utilité des travaux publics », Annales des Ponts et Chaussées, vol. 8, 1844, pp. 332-375
- A. Marshall, Principles of Economics, London, 1890
- A. Mattei, Manuel de microéconomie, Genève, 2000
- Y.O. Vartia, “Efficient Methods of Measuring Welfare Change and Compensated Income in Terms of Ordinary Demand Functions”, Econometrica, vol. 51, 1983, pp.79-98
- R. Willig, « Consumer’s Surplus without Apology », American Economic Review, vol. 66, 1976, pp. 589-597



![{\displaystyle v(p,y)=max[u=u(x)]{\text{ sous la contrainte du budget}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e3125a5110f5e4d015bfbf70f8e7177124723da)



![{\displaystyle S={\frac {1}{\lambda }}\mid -v(p,y)\mid _{p_{1}}^{p_{o}}={\frac {1}{\lambda }}[v(p_{1},y)-v(p_{o},y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffcdeaa81d557ef5b8f2ee127a69a4ebdc4c72af)




