Solénoïde


Un solénoïde (du grec « solen », « tuyau », « conduit », et « eidos », « en forme de[1] ») est un dispositif constitué d'un fil électrique en métal enroulé régulièrement en hélice de façon à former une bobine longue. C'est pourquoi le solénoïde prend aussi le terme de bobine. Parcouru par un courant alternatif ou continu, il produit un champ magnétique dans son voisinage, et plus particulièrement à l'intérieur de l'hélice. La force du champ magnétique dépend le plus souvent de l'intensité du courant, de la nature du noyau et la longueur du fil. C'est au cours de l'année 1820 qu'André-Marie Ampère imagina le nom de solénoïde, lors d'une expérience sur les courants circulaires[2]. Dans l’industrie, le terme solénoïde est aussi utilisé pour se référer à un transducteur. Lorsqu'il est parcouru par une énergie électrique, il va créer une force selon son axe d’enroulement.
Solénoïde fini[modifier | modifier le code]
Champ magnétique sur l'axe[modifier | modifier le code]

Le solénoïde de révolution (circulaire) est modélisé par une série de spires de rayon , de même axe, parcourues par un même courant et disposées régulièrement sur une longueur .
Le champ magnétique créé par une spire de courant sur son axe :
, où est la perméabilité magnétique du vide.
Le champ créé par le solénoïde sur son axe :
.
On procède au changement de variable : , .
On obtient ainsi :
Au centre du solénoïde, c'est-à-dire en x = 0, cette formule devient :
avec , la valeur de en x = 0 et .
En remplaçant par , finalement :
Interprétation : Le champ magnétique créé au centre augmente donc en ajoutant des spires ou en augmentant l'intensité du courant, mais diminue en agrandissant le diamètre du solénoïde.
Remarque : l'expression du champ magnétique pour le solénoïde peut être obtenue à partir du théorème d'Ampère.
Il est aussi possible de déterminer le champ sur l'axe en fonction de la distance x du centre du solénoïde en se positionnant à un point M du centre comme montré sur le schéma ci-contre.

D'où :
En utilisant les formules trigonométriques :
Finalement :
Le graphe ci-dessous représente le champ magnétique sur l'axe d'un solénoïde d'une série de N = 1000 spires de diamètre D = 2 cm, parcourues par un même courant I = 0,2 A et disposées régulièrement sur une longueur l = 80 cm.

Champ magnétique hors de l'axe[modifier | modifier le code]

Les équations que nous allons établir vont permettre de déterminer le champ axial et radial en n’importe quel point de l’espace, à l’intérieur ou à l’extérieur du solénoïde. Considérons un solénoïde de longueur et de rayon .
Le champ magnétique créé par le solénoïde peut être exprimé avec le potentiel vecteur par :
Le potentiel vecteur est un vecteur polaire, c'est-à-dire qu'il appartient à un plan de symétrie de la distribution de courant et est donc perpendiculaire à un plan d’anti-symétrie[3]. Le plan (O,r,z) dans le repère cylindrique est un plan d’anti-symétrie de la distribution de courant. Ainsi, la géométrie du système implique que seule la composante est non nulle. Par conséquent, on peut écrire :
En intégrant les équations de et sur ordinateur, on obtient une description du champ magnétique créé par un solénoïde fini. On peut également exprimer ces équations en fonction d’intégrales elliptiques :
où , est une intégrale elliptique de première espèce et est une intégrale elliptique de deuxième espèce.

où et est la fonction lambda Heuman.
Il est pratique de connaître en particulier la variation du champ près de l’axe du solénoïde. En faisant tendre vers 0, on a :


On constate qu’augmenter la longueur du solénoïde fait décroître la variation radiale du champ axial, c'est-à-dire que le champ axial devient de plus en plus uniforme le long du solénoïde. On retrouve le cas particulier du solénoïde infiniment long.
Pour des solénoïdes de courtes longueurs, le champ axial augmente rapidement du centre du solénoïde vers les extrémités du solénoïde. Au centre, le champ ressemble à celui dû à une simple boucle[4],[5].
On s'aperçoit alors que ce champ est quasi-homogène dans tout le volume délimité par le solénoïde. Cela correspond à des lignes de champ quasi-parallèles entre elles. À l'extérieur du solénoïde, le champ est analogue à celui d'un aimant[note 1].
Modèle du solénoïde infini[modifier | modifier le code]

Un solénoïde est modélisé par une juxtaposition de spires circulaires parcourues par un courant i.
Considérons ici un solénoïde infini constitué de N spires et d'axe de révolution Oz. On cherche à calculer le champ magnétique à l'intérieur du solénoïde. Pour cela on se place en coordonnées cylindriques en considérant la base locale .
En étudiant les symétries et invariances du système, on montre que le champ magnétique est orienté selon , et qu'il ne dépend que de r (la distance à l'axe de révolution), de telle sorte que l'on a :
En appliquant le théorème d'Ampère, on peut calculer le champ magnétique à l'intérieur du solénoïde. Pour cela on définit un contour d'Ampère (contour fermé et orienté) : on considère un rectangle ABCD de longueur AB = l (cf. figure ci-contre). Le rectangle enlace N spires, chacune parcourue par le même courant d'intensité i.
Le théorème d'Ampère appliqué sur le contour ABCD donne :
- est la perméabilité magnétique du vide ;
- i est l'intensité du courant circulant dans une spire ;
- N est le nombre de spires juxtaposées constituant le solénoïde.
La relation de Chasles permet de décomposer l'intégrale en somme de quatre intégrales : .
Or, sur les segments BC et DA, les vecteurs et sont orthogonaux. Par conséquent les intégrales sur ces deux segments sont nulles.
Il reste : .
On peut démontrer que le champ magnétique est nul à l'extérieur d'un solénoïde infini. Par conséquent l'intégrale sur le segment CD (situé à l'extérieur du solénoïde) est nulle.
On a alors : . Et comme le segment AB est de longueur l, on obtient [6].
On remarque que le champ magnétique à l'intérieur du solénoïde est finalement indépendant de r et on a :
Inductance[modifier | modifier le code]
Comme montré ci-dessus, le champ magnétique dans le solénoïde est pratiquement constant. En faisant passer un courant i dans un solénoïde, on obtient un champ magnétique induit de norme égale à :
On cherche ici à calculer l'inductance à partir du flux traversant un solénoïde.
En ignorant les effets de bords du solénoïde, le flux total traversant le solénoïde est obtenu en multipliant le champ B par la section transverse S. En effet, le solénoïde est un dispositif qui capture le flux :
La notion de flux impose qu'il faut prendre en compte la composante de temps. Ceci permet d'induire l'induction magnétique. En effet, lorsque le flux du champ magnétique qui traverse un circuit conducteur varie au cours du temps, il apparaît dans ce circuit une tension appelée force électromotrice e. Ce phénomène est décrit par la loi de Lenz-Faraday.
Or, la tension au bornes d'un solénoïde est aussi égale à : , où L est l'inductance.
La force électromotrice créée est orientée de sorte que le courant généré s'oppose à la variation du flux. On parle ici d'auto-induction. Ceci correspond au fait que la source du champ magnétique à l'origine de la force électromotrice dans un circuit est le courant électrique parcourant ce même circuit. Il y a donc une rétroaction entre le champ magnétique et les variations du courant dans le circuit.
En considérant maintenant un solénoïde dont le courant évolue au cours du temps, comme vu précédemment, cela induit un champ magnétique.
Ici le champ magnétique dynamique est capturé par le solénoïde ce qui en fait un flux. Donc :
En réarrangeant l'équation, on obtient :
- .
Donc par identification avec la formule donnée précédemment , on en déduit l'expression de l'inductance :
L'inductance L qui est donc déterminée par la géométrie du solénoïde mais est indépendante du courant.
Le symbole L qui détermine l'inductance a été choisi en l'honneur de Heinrich Lenz qui a été un des premiers à travailler sur l'inductance électromagnétique[7].
Unités[modifier | modifier le code]
L'unité de l'inductance est le henry (H) en l'honneur de Joseph Henry, un scientifique américain qui a découvert le phénomène d'induction électromagnétique indépendamment des recherches qu'a effectué l'anglais Michael Faraday. On peut exprimer le henry dans les unités du système international en procédant ainsi :
Henry a découvert cette inductance en montrant qu'une variation d'intensité du courant de 1 ampère en 1 seconde provoque l'apparition d'une force électromotrice de 1 volt.
Valeur de l'inductance selon la géométrie[modifier | modifier le code]
Il existe des calculateurs sur Internet pour calculer l'inductance selon la géométrie[8].
Ici nous allons rapidement détailler les formules utilisées pour ces calculs.
- Solénoïde de section S, de nombre de spire N, de longueur l, de nombre de spires par unité de longueur n :
- Un conducteur coaxial :
- .
Par identification, on obtient .
- Un anneau de rayon R :
- .
Par identification on a : .
- Une boucle rectangulaire de largeur w, de hauteur h et de rayon a :
- .
Par identification on a : .
Types de solénoïde et applications[modifier | modifier le code]
Le solénoïde est utilisé dans une multitude d'applications technologiques du fait de ses propriétés électriques et magnétiques. Il peut être utilisé en tant que bobine simple. On peut lui ajouter un noyau de fer doux auquel cas il sera apparenté à un électroaimant. On peut aussi aménager un entrefer dans le noyau qui permet une ouverture indispensable pour des applications de lecture/écriture des appareils tels que : magnétophone à bande magnétique ou disque dur d'ordinateurs.
Les applications du solénoïde sont nombreuses car il est souvent couplé à d'autres composants. En effet, les bobines, associées avec une résistance et/ou un condensateur, sont notamment très utilisées en filtrage : on retrouve souvent des bobines dans les enceintes ou amplificateurs audio. Elle possède aussi des propriétés électromagnétiques car associée à un aimant (électroaimant) ou une autre bobine (transformateur, bobines de Helmholtz...) peut servir de transformateur de tension, de mécanisme de moteur, d'interrupteur ou encore de microphones.
Aujourd'hui, les solénoïdes couplés ou non avec d'autres composants, sont utilisés :
- Dans l'automobile pour des valves hydrauliques ou pneumatiques, pour le verrouillage des sélecteurs de boites de vitesse, pour le contrôle de la climatisation, pour le système de sécurité, ou pour les joy-stick des jeux de simulation de conduite,
- Dans la sécurité pour des mécanismes de fermeture magnétique des portes dans les hôtels, les bureaux ou les zones de surveillance élevée,
- Dans la médecine pour des machines de dialyse ou machine qui sert à contrôler le flux de médicaments injectés dans le sang du patient,
- Dans l'industrie pour le verrouillage, le positionnement, le pincement, le maintien, la rotation, la déviation, le fonctionnement des vannes de plusieurs machines,
- Dans l'agriculture pour le contrôle du flux d'air et d'eau avec des électrovannes par exemple qui contrôlent le flux de l'eau dans les systèmes d'arrosage ou la pression de l'air dans les systèmes de climatisation[9].
Les solénoïdes touchent une grande partie de l'industrie mais leurs applications sont souvent confondues avec celles des électroaimants. C'est pourquoi nous allons traiter les deux cas indépendamment.
Le cas de l'électroaimant[modifier | modifier le code]
Il faut savoir que le solénoïde couplé à un noyau de fer doux génère un électroaimant. Dès que le courant est arrêté le noyau de fer doux perd son aimantation. L'électroaimant est aussi utilisé pour de nombreuses applications et utilise le solénoïde linéaire et le solénoïde rotatif expliqué ci-dessous.
Solénoïde linéaire[modifier | modifier le code]

Quand on impose un courant électrique à travers le fil, un champ magnétique est créé. L’intérieur d’un solénoïde est un cylindre mobile de fer ou d’acier appelé sous différents noms : armature, plongeur ou noyau. Le champ magnétique applique donc une force soit attractive soit répulsive sur l’armature. Cette force est proportionnelle au changement d’inductance de la bobine en prenant en compte le changement de position de l’armature et le courant traversant la bobine (Loi de Faraday sur l’induction). La force appliquée déplacera toujours l’armature dans la direction permettant d’augmenter l’inductance de la bobine. Quand on arrête le courant, le champ magnétique s’arrête et un ressort permet au dispositif de reprendre sa position initiale.
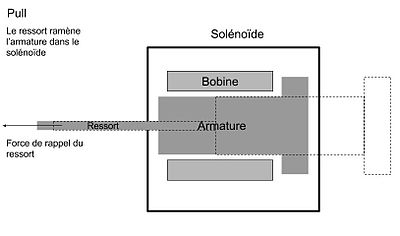
Il existe deux principaux types de solénoïdes linéaires : Push et Pull. Leur nom se réfère à l’action qu’aura la force sur l’armature. Dans le cas du Push, l’armature se trouvera maintenue à l’intérieur du solénoïde à l’aide d’un ressort. Lorsqu’on applique un courant, le champ magnétique va pousser l’armature en dehors du solénoïde. À l’opposé dans le cas d’un Pull, le ressort utilisé maintient l’armature en partie à l’extérieur du solénoïde. Cette fois lorsqu’on applique un courant, la force va attirer l’armature dans le solénoïde. Ainsi, l’armature est utilisée pour apporter une force mécanique à un système comme pour contrôler une valve pneumatique dans l'automobile ou pour le mécanisme de verrouillage d'une porte qui est l'une des meilleures applications de ce type de solénoïde.

Solénoïde rotatif[modifier | modifier le code]
Dans un électroaimant rotatif, nous retrouvons la même configuration de bobinage et d’armature, mais avec une petite modification. Un disque rotatif a été ajouté à la simple structure bobine-armature. L’armature est montée au centre du disque dont la partie inférieure est rainurée. Le corps de l'électro-aimant est aligné sur ses rainures et des roulements à billes facilitent le déplacement. Lorsque le courant est appliqué, l’armature recule dans le bobinage. Cette force linéaire est transférée au disque par les rainures et devient donc une force de rotation. La plupart de ces mécanismes sont équipés d'un ressort. Lorsqu'on arrête le courant, le ressort remet l'armature à sa position initiale hors du bobinage et rétablit la position du disque.
Le cas du solénoïde[modifier | modifier le code]
En considérant le solénoïde seul, on peut lister les applications suivantes :
- Assurer l'élimination des parasites d'une alimentation électrique ou d'un signal analogique, elle joue alors le rôle d'impédance
- Raccourcir une antenne (la bobine joue le rôle d'amplificateur de signal)
- Accorder en impédance un circuit
- Créer un filtre pour une fréquence ou une bande de fréquences particulières
- Lisser les courants continus (le bruit est éliminé) ou contrôler la croissance des courants dans les dispositifs d'électronique de puissance
- Stocker de l'énergie électromagnétique. L'énergie est entièrement stockée dans le champ magnétique dans le noyau de la bobine. On peut alors voir des bobines en supraconducteur, appelées SMES (Superconducting Magnet Energy Storage).
- Servir d'interrupteur commandé dans le cadre de la régulation magnétique. On peut utiliser un transformateur relié à une pile. Lorsqu'on déconnecte la pile, une forte énergie apparait ce qui permet au transformateur de jouer le rôle de survolteur. Si la pile est connectée, la première bobine du transformateur se charge et se décharge dans la seconde bobine lorsqu’on débranche la pile. Ainsi la bobine sert d'interrupteur
- Servir pour l'éclairage par lampes à décharges qui utilisent des ballasts magnétiques et électroniques (lampes fluorescentes, lampes aux halogénures métalliques, etc.)[10].
De nombreuses autres Applications sont détaillées pour les bobines.
Monopôle magnétique, corde de Dirac[modifier | modifier le code]
Si on considère un solénoïde infiniment long de rayon très petit, le champ magnétique dans tout l'espace est celui d'un monopôle magnétique.
L'intérieur du solénoïde constitue une singularité appelée « corde de Dirac », objet irréalisable en pratique mais utile en électrodynamique quantique.
Une description de la corde de Dirac par le biais d'un solénoïde permet surtout la construction d'un potentiel vecteur du champ magnétique dans tout l'espace sauf la corde elle-même[11].
Dans le cas d'un solénoïde , on peut alors définir un potentiel vecteur A tel que : , avec A et B uniformes dans tout l'espace, sauf à l'intérieur du solénoïde.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Pour plus de détails, voir Finite length Solenoid potential and field
Références[modifier | modifier le code]
- Solénoïde, sur le site cnrtl.fr
- Les merveilles de la science Volume 1 (1867) - Louis Figuier, p. 719
- http://physique-univ.fr/onewebmedia/Electromag-c7-site.pdf
- (en) « The magnetic field of a finite solenoid », (consulté le )
- (en) A. K. Al-Shaikhli, H. Fatima, K. Omar et A. Fadhil, « The Magnetic Field Study of a Finite Solenoid », Circuits and Systems, vol. 04, no 03, , p. 316–322 (DOI 10.4236/cs.2013.43043, lire en ligne, consulté le )
- « Théorème d'Ampère appliqué à un solénoïde (2) [Les propriétés du champ magnétostatique] », sur uel.unisciel.fr (consulté le )
- (en) « Inductance – The Physics Hypertextbook », sur The Physics Hypertextbook (consulté le ).
- « Missouri S&T », sur emclab.mst.edu (consulté le )
- (en) « Solenoid Applications in the Modern World »
- « Bobines »
- (en) « What is an intuitive explanation of a Dirac string? », sur Quora.com
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- John David Jackson (trad. de l'anglais), Électrodynamique classique [« Classical Electrodynamics »] [détail de l’édition]
- Alfred S. Goldhaber et W. Peter Trower, « Resource Letter MM‐1: Magnetic monopoles », in American Journal of Physics, Volume 58, no 5,
- Edmund E. Callaghan et Stephen H. Maslen, The magnetic field of a finite solenoid, NASA Technical note D-465
- A.K. Al-Shaikhli, H. Fatima, K. Omar, A. Fadhil, J. Lina, The Magnetic Field Study of a Finite Solenoid







































![{\displaystyle A_{\theta }={\frac {a\mu nI}{2\pi }}\int _{0}^{\pi }cos\theta \ln \left[\xi +{\sqrt {\xi ^{2}+r^{2}+a^{2}-2arcos\theta }}\right]_{\xi _{-}}^{\xi _{+}}d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa49c7d64ed43f8d9408ea8b9bb53d20faf1664b)
![{\displaystyle A_{\theta }={\frac {a\mu nI}{2\pi }}\left[sin\theta \ln \left[\xi +{\sqrt {\xi ^{2}+r^{2}+a^{2}-2arcos\theta }}\right]_{\xi _{-}}^{\xi _{+}}\right]_{\theta =0}^{\theta =\pi }-{\frac {a\mu nI}{2\pi }}\int _{0}^{\pi }\left[{\frac {arsin^{2}\theta d\theta }{(\xi +{\sqrt {\xi ^{2}+r^{2}+a^{2}-2arcos\theta }}){\sqrt {\xi ^{2}+r^{2}+a^{2}-2arcos\theta }}}}\right]_{\xi _{-}}^{\xi _{+}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e9f50ee80ae654343426d854f3a056791484a1a)

![{\displaystyle A_{\theta }={\frac {a^{2}\mu nIr}{2\pi }}\int _{0}^{\pi }\left[{\frac {\xi sin^{2}\theta d\theta }{(a^{2}+r^{2}-2arcos\theta ){\sqrt {\xi ^{2}+r^{2}+a^{2}-2arcos\theta }}}}\right]_{\xi _{-}}^{\xi _{+}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/817169df2b5d994a984f3db3a9e9709ba4f1e416)

![{\displaystyle B_{r}=-{\frac {\partial A_{\theta }}{\partial z}}=-{\frac {\partial }{\partial z}}\left({\frac {a\mu nI}{2\pi }}\int _{\xi _{-}}^{\xi _{+}}d\xi \int _{0}^{\pi }{\frac {cos\theta d\theta }{\sqrt {\xi ^{2}+r^{2}+a^{2}-2arcos\theta }}}\right)=-{\frac {a\mu nI}{2\pi }}\int _{0}^{\pi }\left[{\frac {cos\theta d\theta }{\sqrt {\xi ^{2}+r^{2}+a^{2}-2arcos\theta }}}\right]_{\xi _{-}}^{\xi _{+}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d839047b84f856111ca8163989a2a1ece8be0e2)


![{\displaystyle {\frac {\partial A_{\theta }}{\partial r}}=-{\frac {a\mu nI}{2\pi }}\int _{0}^{\pi }\left[{\frac {\xi cos\theta (r-acos\theta )d\theta }{(r^{2}+a^{2}-2arcos\theta ){\sqrt {\xi ^{2}+r^{2}+a^{2}-2arcos\theta }}}}\right]_{\xi _{-}}^{\xi _{+}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8921fc21ce832fe12dc60125237299daef04c8bc)
![{\displaystyle B_{z}={\frac {1}{r}}{\frac {\partial (rA_{\theta })}{\partial r}}={\frac {a\mu nI}{2\pi }}\int _{0}^{\pi }\left[{\frac {\xi (a-rcos\theta )d\theta }{(r^{2}+a^{2}-2arcos\theta ){\sqrt {\xi ^{2}+r^{2}+a^{2}-2arcos\theta }}}}\right]_{\xi _{-}}^{\xi _{+}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f20ce554c25d565b1ddba05812d1601ab08cdbdf)
![{\displaystyle B_{r}=-{\frac {\mu nI}{\pi }}{\sqrt {\frac {a}{r}}}\left[{\frac {2-k^{2}}{2k}}K(k)-{\frac {E(k)}{k}}\right]_{\xi _{-}}^{\xi _{+}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32644cbd10976878a4426341e2423643c7b30bdc)



![{\displaystyle B_{z}={\frac {\mu nI}{4}}\left[{\frac {\xi k}{\pi {\sqrt {ar}}}}K(k)+{\frac {(a-r)\xi }{|(a-r)\xi |}}\lambda _{0}(\phi ,k)\right]_{\xi _{-}}^{\xi _{+}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c798df29a5b7174b1ed4d493697beebcf1800278)



![{\displaystyle B_{r}={\frac {\mu nI}{4}}\left[{\frac {a^{2}r}{(\xi ^{2}+a^{2})^{3/2}}}\right]_{\xi _{-}}^{\xi _{+}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3892007177ce1e1c357e44b5937f8d6502a885e)
![{\displaystyle B_{z}={\frac {\mu nI}{2}}\left[{\frac {\xi }{\sqrt {\xi ^{2}+a^{2}}}}\right]_{\xi _{-}}^{\xi _{+}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/661d515539b63913ac2b84c7ac07543d3c8842d3)





















![{\displaystyle {\rm {\left[H={\frac {V}{A/s}}={\frac {J/C}{A/s}}={\frac {kg\cdot m^{2}\cdot s^{-2}/(A\cdot s)}{A\cdot s^{-1}}}={\frac {kg\cdot m^{2}}{A^{2}\cdot s^{2}}}={\frac {kg\cdot m^{2}}{C^{2}}}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8c6edad32c16ae81532dc467eaceccd033908d0)






![{\displaystyle L={\frac {\mu _{0}N^{2}}{\pi }}\left[y\,\ln \left({\frac {x}{a}}\right)+x\,\ln \left({\frac {y}{a}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d1c0246bb49d68e22efcc4e3d4e60d4bb0cda6)

