Plus longue sous-chaîne commune

Cet article est une ébauche concernant l’informatique.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

En informatique, le problème de la plus longue sous-chaîne commune, à ne pas confondre avec celui de la plus longue sous-séquence commune, consiste à déterminer la (ou les) plus longue(s) chaîne(s) consécutives de caractères qui est sous-chaîne de deux chaînes de caractères. Ce problème se généralise à la recherche de la plus longue sous-chaîne commune à plus de deux chaînes de caractères.

Exemple[modifier | modifier le code]

La plus longue sous-chaîne commune à « ABABC », « BABCA » et « ABCBA » est la chaîne « ABC » de longueur 3. Les autres sous-chaînes communes telles que « AB », « BC » et « BA » sont plus courtes.

  ABABC
    |||
   BABCA
    |||
    ABCBA

Formalisation du problème[modifier | modifier le code]

Étant donné deux chaînes, $S$ de longueur $n$ et $T$ de longueur $m$ , trouver la plus longue chaîne étant en même temps sous-chaîne de $S$ et $T$ . Par définition la longueur de la plus longue sous-chaîne est comprise entre $0$ (vocabulaires disjoint) et $max(n,m)$ ( $S=T$ ).

Algorithmes[modifier | modifier le code]

Il est possible de déterminer la longueur et la position de départ de la plus longue sous-chaîne de $S$ et $T$ en $\Theta (n+m)$ à l'aide d'un arbre des suffixes généralisé (en). L'algorithme naïf faisant appel à la programmation dynamique est beaucoup plus coûteux en temps : $\Theta (nm)$ .

Arbre des suffixes[modifier | modifier le code]

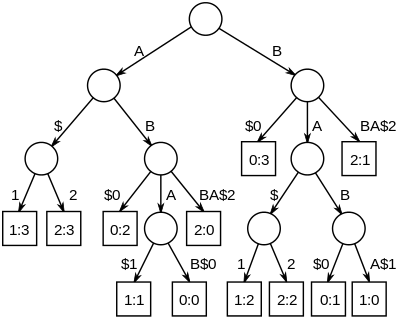
La plus longue chaîne commune à un ensemble de chaînes peut être déterminée en construisant l'arbre des suffixes généralisé puis en trouvant le nœud le plus profond ayant des feuilles pointant vers toutes les chaînes. Dans l'exemple ci-contre, le nœud auquel on arrive par « AB » a quatre feuilles dans son sous-arbre ; la feuille de gauche dit qu'une occurrence de la sous-chaîne « AB » commence en position 2 dans la chaîne 0 (« ABAB »), de même, la feuille de droite indique une occurrence débutant en position 0 dans la chaîne 2 (« ABBA ») ; des deux feuilles centrales, celle de gauche indique qu'une occurrence de la sous-chaîne « ABA » commence en position 1 dans la chaîne 1 (« BABA »).

La construction de l'arbre des suffixes a une complexité en temps de $\Theta (N)$ , où $N$ est la somme des longueur des chaînes représentées.

La recherche peut se faire en temps similaire grâce à des algorithmes de plus petit ancêtre commun^[1].

Programmation dynamique[modifier | modifier le code]

Dans un premier temps, on cherche le plus long suffixe commun pour chaque paire de préfixes des deux chaînes $S$ et $T$ . Le plus long suffixe commun du préfixe $S[1,p]$ de longueur $p$ de $S$ et du préfixe $T[1,q]$ de longueur $q$ de $T$ est

{\mathsf {PLSuff}}(S[1,p],T[1,q])={\begin{cases}{\mathsf {PLSuff}}(S[1,p-1],T[1,q-1])+1&{\text{si }}S[p]=T[q]\\0&{\text{sinon}}.\end{cases}}

Pour les chaînes « ABAB » et « BABA », on obtient:

	A	B	A	B
	0	0	0	0
B	0	1	0	1
A	1	0	2	0
B	0	2	0	3
A	1	0	3	0

Le plus grand de ces suffixes communs à tous les préfixes est la plus longue sous-chaîne commune. Dans la table, elles sont indiquées en rouge, et dans l'exemple, les deux sous-chaînes communes de longueur maximale sont « ABA » et « BAB ».

{\mathsf {PLSC}}(S,T)=\max _{1\leq p\leq m \atop 1\leq q\leq n}{\mathsf {PLSuff}}(S[1,p],T[1,q]).

La méthode peut être étendue à plus de deux chaînes en ajoutant des dimensions à la table.

Notes et références[modifier | modifier le code]

↑ (en) Dan Gusfield, Algorithms on Strings, Trees and Sequences : Computer Science and Computational Biology, Cambridge/New York/Melbourne, Cambridge University Press, 1999, 534 p. (ISBN 0-521-58519-8, lire en ligne)

Liens externes[modifier | modifier le code]

Sur les autres projets Wikimedia :

Plus longue sous-chaîne commune, sur Wikibooks

Source de la traduction[modifier | modifier le code]

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Longest common substring problem » (voir la liste des auteurs).

Voir également[modifier | modifier le code]

Portail de l’informatique

[1] (en) Dan Gusfield, Algorithms on Strings, Trees and Sequences : Computer Science and Computational Biology, Cambridge/New York/Melbourne, Cambridge University Press, 1999, 534 p. (ISBN 0-521-58519-8, lire en ligne)

[1]

v · m Algorithmique du texte
Recherche de sous-chaîne	Algorithme de Knuth-Morris-Pratt Algorithme de Boyer-Moore Algorithme de Boyer-Moore-Horspool Algorithme de Raita Algorithme de Baeza-Yates-Gonnet Algorithme Z Algorithme de Rabin-Karp Algorithme d'Aho-Corasick
Alignement de chaînes	Algorithme de Needleman-Wunsch Algorithme de Smith-Waterman Transformée de Burrows-Wheeler
Mesure de similarité	Distance de Jaro-Winkler Distance de Levenshtein Distance de Hamming
Arbre des suffixes	Algorithmes de Weiner et de McCreight Algorithme d'Ukkonen Tableau des suffixes Tableau de Lyndon
Comparaisons	Plus longue sous-séquence commune Plus longue sous-chaîne commune Plus courte super-séquence commune