Observateur d'état
En automatique et en théorie de l'information, un observateur d'état est une extension d'un modèle représenté sous forme de représentation d'état. Lorsque l'état d'un système n'est pas mesurable, on conçoit un observateur qui permet de reconstruire l'état à partir d'un modèle du système dynamique et des mesures d'autres grandeurs.
Historique[modifier | modifier le code]
La théorie de l' observateur d'état a tout d'abord été introduite par Kalman et Bucy pour un système linéaire dans un environnement stochastique (Filtre de Kalman-Bucy)[1],[2]. Puis Luenberger (en) a fait une théorie générale des observateurs pour les systèmes linéaires déterministes, introduisant notamment les notions d'observateur réduit et d'observateur minimal[3],[4]. Les observateurs linéaires ont donné lieu à des travaux récents, allant vers une généralisation toujours plus poussée[5],[6]. Pour les systèmes non linéaires, le filtre de Kalman étendu[7] reste très utilisé malgré les résultats importants obtenus récemment sur les observateurs non linéaires à grand gain[8]. Une problématique très importante est celle de la robustesse des observateurs. Un apport fondamental est celui de Doyle et Stein, avec le procédé LTR ("Loop Transfer Recovery")[9],[10] dont une interprétation entièrement algébrique a pu être donnée dans le cas monovariable[11],[12].
Position du problème[modifier | modifier le code]
Considérons le système linéaire suivant :
La mise en œuvre de la commande par retour d'état a besoin de capteurs permettant de donner à chaque instant une valeur approximative de l'état . Deux types de capteurs de natures différentes sont utilisés. Le premier est celui des capteurs physiques, provenant de l'instrumentation. Ces capteurs sont parfois trop coûteux ou difficiles à réaliser pour des raisons techniques. On peut donc être amené à concevoir un second type de capteurs—des capteurs logiciels, appelés plus communément des observateurs. Ces derniers sont des algorithmes fondés sur un modèle du système et utilisant une information pertinente donnée par des capteurs physiques. Ces capteurs logiciels délivrent à chaque instant une estimation en ligne des variables d'état non mesurées du système.
Architecture avec un observateur[modifier | modifier le code]
Si désigne l'état (non mesuré) du système, représente l'estimation de l'état faite par l'observateur.
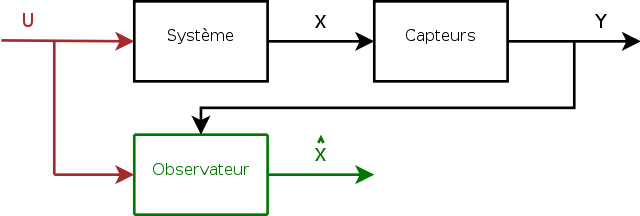
L'estimation de l'état se fait en recopiant de façon virtuelle la dynamique du système en prenant en compte non seulement la commande , mais aussi les sorties du système (les mesures) dans le but de corriger les écarts éventuels.
Observateur d'état complet[modifier | modifier le code]
Soit le système linéaire suivant :
Un observateur dynamique a la forme suivante :
On vient corriger l'évolution de l'état grâce au modèle en fonction de l'écart constaté entre la sortie observée et la sortie reconstruite par l'observateur : .
On peut réécrire l'observateur de la manière suivante :
on vérifie bien que l'observateur reconstruit l'état en fonction de la commande et des mesures comme sur le schéma ci-dessus.
La matrice est appelée matrice de gain et doit être choisie de manière que l'erreur sur l'état converge exponentiellement vers 0, soit . Pour cela, il faut et il suffit que soit choisie telle que la matrice ait toutes ses valeurs propres dans le demi-plan gauche (dans le cas discret, cette matrice devrait avoir toutes ses valeurs propres à l'intérieur du disque unité). Une condition nécessaire et suffisante pour qu'une telle matrice existe est que le système soit détectable. Une condition nécessaire et suffisante pour que les valeurs propres de soient placées dans un ensemble symétrique (par rapport à l'axe réel) arbitraire de nombres complexes est que le système soit observable.
Commande par retour d'état reconstruit par un observateur d'état complet[modifier | modifier le code]
L'observateur ci-dessus possède une caractéristique intéressante connue sous le nom de Principe de séparation : dans le cas d'une commande linéaire, on peut concevoir séparément une commande à retour d'état (en supposant l'état connu) et un observateur d'état complet. En effet, si le système muni du retour d'état est stable, et si l'observateur conçu est stable lui aussi (i.e. les valeurs propres des matrices et celles de sont dans le demi-plan gauche) alors le système commandé par retour de l'état reconstruit est stable.
En effet, considérons le système linéaire invariant suivant, observable et commandable, ainsi que l'observateur d'état complet :
En réalisant un bouclage , la dynamique du système bouclé s'écrit alors :
On peut faire le changement de variable suivant, pour écrire l'erreur de reconstruction :
En écrivant un nouveau système augmenté, constitué de l'état et de l'erreur de reconstruction, on obtient :
Cette matrice est triangulaire par blocs, et par conséquent le spectre du système bouclé est constitué de la réunion disjointe des spectres des blocs diagonaux, c’est-à-dire l'union des spectres du système initial commandé, et du système initial observé. Ainsi la synthèse d'un système commandé par un retour d'état reconstruit par un observateur est particulièrement simple pour les systèmes linéaires invariants, puisqu'on peut synthétiser les deux fonctions séparément.
Remarques finales[modifier | modifier le code]
- La commande par retour d'état, quand on n'y adjoint pas un bouclage intégral, constitue un piètre asservissement. Il en est évidemment de même d'une commande par retour d'état reconstruit. Si donc désigne le signal de référence et est l'erreur de consigne, la commande mise en œuvre sera finalement de la forme (à une constante additive près)
- Tandis que les pôles de la commande à retour d'état et bouclage intégral doivent être choisis en fonction des pôles du système en boucle ouverte, ceux de l'observateur doivent être choisis en fonction des zéros de ce système. C'est ce qui résulte de l'algébrisation de la « méthode LTR » évoquée dans l'historique, et qui s'étend au cas où un bouclage intégral est utilisé[12]. Le système en boucle ouverte ayant toujours certains zéros à l'infini, les pôles correspondants de l'observateur seront choisis « suffisamment rapides », notamment par rapport aux autres pôles de la boucle fermée. Ceci conduit à nuancer le Principe de séparation : ce dernier est pleinement valide pour la stabilité du système bouclé à modèle parfait, mais dès que l'on prend en compte la problématique de la robustesse, la question devient un peu plus complexe. D'autre part, les zéros finis du système en boucle ouverte doivent idéalement être des pôles de l'observateur. Ce dernier devant être stable, cela n'est possible que si ces zéros sont « stables » (i.e., dans le demi-plan gauche ouvert dans le cas du temps continu, à l'intérieur du cercle unité dans le cas du temps discret). La situation où cette condition n'est pas remplie est défavorable, indépendamment de la méthode choisie pour réaliser l'asservissement[13].
- L'observateur est également utilisé en traitement du signal pour filtrer des mesures. C'est dans ce contexte que Kalman a proposé le filtre qui porte désormais son nom.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
Références[modifier | modifier le code]
- (en) Ingrid Blumthaler et Ulrich Oberst, « T-observers », Linear Algebra Appl., vol. 430, nos 8-9, , p. 2416–2447
- (en) Henri Bourlès, Linear Systems, John Wiley & Sons, , 544 p. (ISBN 978-1-84821-162-9 et 1-84821-162-7)
- Henri Bourlès et Ernest Irving, « La méthode LQG/LTR: une interprétation polynômiale temps continu/temps discret », APII, vol. 25, , p. 545–592
- (en) John C. Doyle et Gunther Stein, « Robustness with Observers », IEEE Transaction on Automatic Control, vol. 24, , p. 607-611
- (en) John C. Doyle et Gunther Stein, « Multivariable Feedback Design: Concepts for a Classical/Modern Synthesis », IEEE Transaction on Automatic Control, vol. 26, , p. 4-16
- (en) James S. Freudenberg et Douglas P. Looze, Frequency Domain Properties of Scalar and Multivariable Feedback Systems, Springer, , 281 p. (ISBN 3-540-18869-X)
- (en) Paul A. Fuhrmann, « Observer theory », Linear Algebra Appl., vol. 428, no 1, , p. 44–136
- (en) Jean-Paul Gauthier et Ivan Kupka, Deterministic observation theory and applications, Cambridge University Press, , 238 p. (ISBN 978-0-521-18386-4 et 0-521-18386-3)
- (en) A. Gelb, Applied Optimal Estimation, MIT Press, (réimpr. 1996), 382 p. (ISBN 0-262-57048-3)
- (en) Rudolf E. Kalman, « A New Approach to Linear Filtering and Prediction Problems », Transactions of the ASME - Journal of Basic Engineering, vol. 82, , p. 35-45
- (en) Rudolf E. Kalman et Richard S. Bucy, « New Results in Linear Filtering and Prediction Theory », Transactions of the ASME - Journal of Basic Engineering, vol. 83, , p. 95-107
- (en) David G. Luenberger, « Observing the state of a linear system », IEEE Transaction on Military Electronics, vol. 8, , p. 74-80
- (en) David G. Luenberger, « An Introduction to Observers », IEEE Transaction on Automatic Control, vol. 16, , p. 596-602

























