Méthode de Heun

En mathématiques et en informatique, la méthode de Heun est une méthode de résolution numérique des équations différentielles ordinaires à conditions initiales. Elle étend et améliore la méthode d'Euler, et fait partie de la classe plus générale des méthodes de Runge-Kutta d'ordre deux.

Soit l'équation différentielle avec conditions initiales  :

$y'(t)=f(t,y(t)),\qquad \qquad y(t_{0})=y_{0},$

La méthode de Heun calcule itérativement des valeurs successives de y à des valeurs données du paramètre t_i, à partir de la initiale de y connue en t = t₀.

À chaque nouvelle itération, la méthode procède en deux temps en calculant une première estimation ${\tilde {y}}_{i+1}$, obtenue par la formule de la méthode d'Euler puis en la corrigeant pour obtenir l'approximation finale $y_{i+1}$ au prochain point d'intégration.

${\tilde {y}}_{i+1}=y_{i}+hf(t_{i},y_{i})$

$y_{i+1}=y_{i}+{\frac {h}{2}}[f(t_{i},y_{i})+f(t_{i+1},{\tilde {y}}_{i+1})],$

où $h$ est la taille de l'intervalle telle que $t_{i+1}=t_{i}+h$ .

Description

La méthode d'Euler utilise uniquement la valeur de la dérivée à l'extrémité inférieure de l'intervalle [t_i, t_i+1] pour estimer la pente de la courbe sur l'intervalle. Si la largeur de l'intervalle, c'est à dire le pas d'intégration h est est suffisamment petit, alors l'erreur sera faible. Cependant, les erreurs peuvent s'accumuler à chaque nouvelle itération d'intégration et faire diverger la solution numérique par rapport à la vraie valeur de la fonction cherchée.

Diagramme illustrant l'utilisation de la méthode de Heun pour trouver une meilleure prédiction par rapport à la méthode d'Euler.

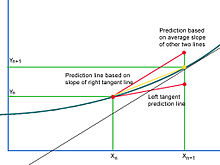
Par exemple, si la solution est une fonction convexe, la tangente en un point est toujours sous la courbe de la fonction. En utilisant uniquement la dérivée en ce point, on sera amener à toujours sous-estimer l’ordonnée du prochain point, et cette sous-estimation ira en s'accumulant au fil des itérations. L'inverse se produit si la fonction est concave.

La méthode de Heun tente de corriger ce problème en utilisant une meilleure estimation de la tangente sur le segment entier. On l'obtient calculant une deuxième valeur de la pente de la tangente à l'autre extrémité t_i+1de l'intervalle, que l'on estime à l'aide de la méthode d'Euler. Dans le cas de l'exemple convexe, cette deuxième valeur sera toujours sur-estimée. L'idée de la méthode de Heun est donc de prendre la moyenne de ces deux estimations.

La précision de la méthode d'Euler s'améliore linéairement par rapport à la taille du pas, alors que la méthode de Heun bénéficie d'une progression quadratique.

La méthode s'apparente à la méthode des trapèzes qui est une méthode implicite utilisant la dérivée exacte $f(t_{i+1},y_{i+1})$. Dans la méthode de Heun, cette valeur est remplacée par l'estimation $f(t_{i+1},{\tilde {y}}_{i+1})$ afin de la rendre explicite, c'est à dire de ne pas exiger une résolution d'équation.

Comme vu précédemment, ${\tilde {y}}_{i+1}$ est le résultat obtenu par la méthode d'Euler sur le même problème. Ainsi, la méthode de Heun est une méthode prédictive-correctrice avec méthode d'Euler explicite comme prédicteur et la méthode des trapèzes comme correcteur.

On peut la comparer à la méthode du point médian qui utilise l'estimation de la tangente au milieu de l'intervalle plutôt qu'à ses deux extrémités.

Méthodes de Runge-Kutta

La méthode de Heun est un cas particulier des méthode de Runge–Kutta à deux étapes et peut être décrite en utilisant un tableau de Butcher (d'après John C. Butcher ) :

	0
	1	1
		1/2	1/2

Une méthode apparentée connue sous le nom de méthode de Ralston a pour tableau de Butcher :

	0
	2/3	2/3
		1/4	3/4