Facteur de qualité
Le facteur de qualité (ou facteur Q) d'un système est une mesure sans unité du taux d'amortissement d'un oscillateur. Q est défini de manière générale par un rapport d'énergie :
où est l'énergie maximale contenue dans le système et est l'énergie dissipée par le système sur une période.
Plus le facteur de qualité est élevé, plus les oscillations d'un résonateur libre vont perdurer.
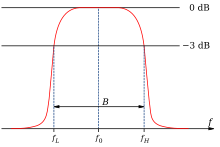
Q peut aussi être défini comme le rapport de la fréquence propre (fréquence à laquelle le gain est maximal) à la largeur de la bande passante de la résonance du système :
Plus le facteur de qualité est élevé, plus la bande passante est petite, et plus la résonance est « piquée ». Le facteur de qualité permet donc de quantifier la « qualité d'un filtre » (qu'il soit électronique, acoustique, optique, etc.) : plus Q est élevé, plus le filtre est sélectif.
Q peut aussi être déterminé à partir de l'équation différentielle régissant l'évolution du système, en la mettant sous forme canonique. Le facteur de qualité permet de déterminer la nature du régime transitoire d'un système oscillatoire (apériodique, critique ou pseudo-périodique).

Lien avec d'autres grandeurs[modifier | modifier le code]
Facteur de qualité d'un oscillateur électrique[modifier | modifier le code]
Dans le cas d'un oscillateur électrique, le facteur de qualité vaut , où est la pulsation propre de l'oscillateur (exprimée en rad/s) et est la constante de temps caractérisant l'amortissement exponentiel de l'énergie dans les oscillations du régime transitoire. Cette constante de temps est la moitié de la constante de temps caractérisant l'amortissement exponentiel du courant ou de la tension pendant les oscillations du régime transitoire : .
Facteur de qualité d'un oscillateur optique[modifier | modifier le code]
Le facteur de qualité d'une cavité optique résonante telle que celle d'un interféromètre de Fabry-Perot peut être défini en fonction du temps de vie des photons dans la cavité :
ou bien en fonction de l'intervalle spectral libre de la cavité ISL et de la finesse F :
.
Facteur de qualité d'un filtre électronique[modifier | modifier le code]
Le facteur de qualité représente la sélectivité du filtre passe bande :
où : fréquence à laquelle le gain est maximal,
et : bande passante du filtre à son atténuation maximale.
Facteur de qualité et oscillateur harmonique amorti[modifier | modifier le code]
Un oscillateur harmonique amorti peut être caractérisé par une grandeur appelée son taux d'amortissement. Cette grandeur, généralement notée , est liée au facteur de qualité par la relation suivante :
Équations différentielles[modifier | modifier le code]
En physique, un grand nombre de problèmes peuvent être modélisés par des équations différentielles linéaires du second ordre ; c’est le cas par exemple de l’évolution de la tension aux bornes d’un dipôle dans un circuit RLC, et d’autres oscillateurs. Il est alors généralement possible de ramener cette équation à la forme canonique suivante :
- ,
où est la grandeur étudiée en fonction du temps et la pulsation propre du système, exprimée en radians par seconde. est une grandeur strictement positive sans dimension, appelée facteur de qualité ; il détermine le signe du discriminant de l’équation quadratique associée et par conséquent la nature des solutions de l’équation homogène, correspondant au régime transitoire.
Ainsi, si , l’espace des solutions de l’équation homogène est de la forme , ce qui correspond à un régime apériodique. Si , le régime transitoire est dit critique, les solutions appartiennent à l’ensemble . Enfin, si , le régime transitoire est pseudopériodique, et les fonctions solutions de l’équation homogène se trouvent dans . Les constantes , , et sont des durées d’amortissement, et une pulsation, qui dépendent exclusivement de et .
En régime pseudopériodique, le temps d’amortissement augmente avec le facteur de qualité ; l’oscillateur s’approche du modèle de l’oscillateur harmonique lorsque tend vers .
Graphiquement[modifier | modifier le code]
Le facteur de qualité peut également être évalué à partir du graphique représentant l'amplitude des oscillations amorties en fonction du temps. La constante de temps des oscillations est l'instant où la tangente initiale de l'enveloppe exponentielle intercepte l'axe des abscisses. On compte ensuite le nombre d'oscillations pseudo-périodiques qui se produisent pendant cette durée, et on utilise la définition .
NB : ceci suppose implicitement que la pulsation du régime transitoire est égale à la pulsation propre du filtre. Ce n'est exact que pour les facteurs de qualité élevés, car à cause de l'amortissement, la pseudo-période des oscillations transitoires est légèrement plus longue que la période propre.
Références[modifier | modifier le code]
Voir aussi[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- Notices dans des dictionnaires ou encyclopédies généralistes :




































