Erreur de mesure

Une erreur de mesure, dans le langage courant, est « la différence entre la valeur donnée par la mesure et la valeur exacte (bien souvent inconnue) d'une grandeur[1],[N 1]. »
Exemples usuels et fictifs d'après cette définition :
- L'indication d'une balance de ménage pour une masse de 1 kg certifiée est de 990 g. L'erreur de mesure est de –10 g ;
- La distance entre deux murs, donnée par un télémètre laser est de 4,485 m, valeur considérée ici comme exacte. La valeur mesurée, au même endroit, avec un mètre à ruban est de 4,5 m. L'erreur de mesure, avec le mètre à ruban, est de 0,015 m ou 1,5 cm ;
- La différence sur 24 heures de temps entre une pendule radio pilotée et une montre bracelet est de 3 s. L'erreur d'indication de la montre est de 3 s. Il est vraisemblable que son avance sera de 6 s sur deux jours et de 1 min sur 20 jours… ;
- l'erreur absolue est l'ancienne appellation de l'erreur de mesure, elle n'est plus d'usage actuel[2] ;
- rapportée à la valeur de la grandeur mesurée, l'erreur relative serait respectivement pour les exemples précédents de 1 % ; 0,33 % ; ≈ 3,5 pour 100 000.
D'autres sources que celle citée, donnent des définitions différentes de l'erreur de mesure[N 2], entrainant des difficultés d'interprétation.
Devant cette confusion et la croissance des échanges de biens au niveau mondial, des organisations internationales (ISO, BIPM…) ont proposé, dès 1984, un vocabulaire international de métrologie, le VIM[3], qui définit et précise les termes à employer en métrologie. L'erreur de mesure est incluse dans ce vocabulaire ; c'est la principale référence de l'article.
Définition[modifier | modifier le code]
En métrologie, dans un mesurage, une erreur de mesure est la « différence entre la valeur mesurée d'une grandeur et une valeur de référence »[4].
- un mesurage peut être composé de une ou plusieurs valeurs mesurées. Dans l'introduction chaque exemple comporte une seule mesure ;
- la valeur mesurée est « la valeur d'une grandeur représentant un résultat de mesure » (VIM 2.10). Dans les exemples précédents, les valeurs mesurées sont respectivement : 990 g ; 4,5 m ; le troisième exemple ne précise pas la valeur mesurée ;
- la valeur de référence peut être :
- le plus souvent, « un étalon qui est la réalisation de la définition d'une grandeur donnée, avec une valeur déterminée et une incertitude de mesure associée » (VIM 5.1),
- plus rarement, « la valeur d'une grandeur servant de base de comparaison pour les valeurs de grandeurs de même nature » (VIM 5.18) : un matériau de référence certifié, un dispositif particulier comme un laser stabilisé, une procédure de mesure de référence (VIM 5.18)… Dans les exemples précédents les valeurs de référence sont respectivement : une masse de 1 kg qui peut être considéré comme étalon, une longueur mesurée de 4,485 m avec un dispositif à laser ; un instrument (pendule) de référence.
Note 1 : le concept d'erreur peut être utilisé lorsqu'il existe une valeur de référence unique à laquelle se rapporter, ce qui a lieu si on effectue un étalonnage au moyen d'un étalon dont la valeur mesurée a une incertitude de mesure négligeable [par rapport au résultat attendu]… (VIM 2.16)[N 3].
Note 2 : Il convient de ne pas confondre l'erreur de mesure avec une erreur de production ou une erreur humaine (VIM 2.16) :
- exemple d'erreur de production : soit à réaliser en série un axe de diamètre 20 ± 0,1 mm. On emploie pour vérifier les pièces un instrument dont l'incertitude est par exemple de ± 0,01 mm. Une pièce particulière a une valeur mesurée de 20,15 mm. L'erreur de production par rapport à la valeur nominale visée de 20 mm est de 0,15 mm ; elle provient certainement d'une cause inhérente à la production : réglage, usure d'outil, etc. L'erreur de mesure concernant la pièce de 20,15 mm (par rapport à sa valeur vraie ) est inconnue ; on peut juste supposer qu'elle est dans l'intervalle d'incertitude de l'instrument, soit ± 0,01 mm ;
- exemples d'erreur humaine :
- Erreur de lecture d'un instrument à cadran ;
- Mesure du diamètre d'une pièce de grandes dimensions à la sortie d'une machine travaillant avec un outil céramique : sans lubrification, la pièce peut atteindre et dépasser les 100 °C ; la dilatation joue alors sur la dimension mesurée de la pièce (la température de référence est de 20 °C).
Causes d'erreurs[modifier | modifier le code]
Lors de la mise en œuvre d'un processus de mesure, conduisant à une valeur mesurée, interviennent des erreurs élémentaires qui affectent le résultat.
Ces erreurs élémentaires peuvent être mises en évidence par l'expérience[5] :
- la répétition des mesures, sans rien changer au processus, conduit à des indications différentes — phénomène bien connu des métrologues. Cette variation des résultats, dont les causes sont rarement connues porte le nom d'erreur aléatoire ;
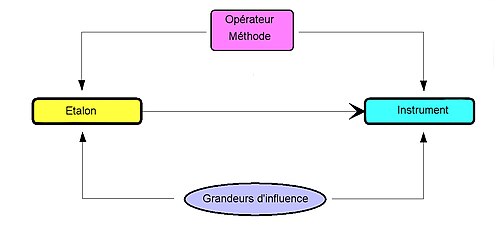
- une variation maitrisée des conditions de l'expérience peut mettre en évidence des erreurs élémentaires dues aux facteurs inhérents au système du processus de mesure (les 5 M bien connus : mesurande, moyen de mesure, main d'œuvre ou opérateur, méthode, milieu). Quelques exemples liés aux 5 M : mise en place pièce sans application, moyens de mesures de même type mais différents, pressions variables sur les instruments exercées par l'opérateur (ou les opérateurs, dans le cadre d'un travail en série avec plusieurs équipes ), méthodes différentes comme la vitesse d'accostage de l'instrument et, pour finir, des variations dues au milieu appelées d'ailleurs « facteurs d'influence », comme la température, l'humidité, les vibrations… La variation de ces derniers résultats, dont les causes peuvent être cernées, porte le nom d'erreur systématique.
Analyse de l'erreur[modifier | modifier le code]
Expression[modifier | modifier le code]
L'erreur de mesure s'exprime par la relation
Exemple :
| Valeur mesurée d'une cale étalon avec un micromètre | X = 25,012 mm |
| Valeur de référence unique de la cale étalon[N 4] | R = 25 mm |
| Erreur de mesure Δ = X - R | Δ = 0,012 mm |
Cette erreur de mesure comprend deux composantes : une composante aléatoire ΔA et une composante systématique ΔS.
Des relations précédentes on tire
Erreur aléatoire[modifier | modifier le code]
« Composante de l'erreur de mesure qui, dans des mesurages répétés, varie de façon imprévisible[6].
NOTE 1 La valeur de référence pour une erreur aléatoire est la moyenne qui résulterait d'un nombre infini de mesurages répétés du même mesurande… »
Erreur systématique[modifier | modifier le code]
« Composante de l'erreur de mesure qui, dans des mesurages répétés, demeure constante ou varie de façon prévisible[7].
NOTE 1 La valeur de référence pour une erreur systématique est une valeur vraie, une valeur mesurée d'un étalon dont l'incertitude de mesure est négligeable… »
Remarque : on trouve aussi la terminologie « erreur de justesse[8] » ou « biais » qui est l'estimation d'une erreur systématique.

Exemple[modifier | modifier le code]
Exemple industriel fictif : étalonnage partiel d'une colonne de mesure, sur une cale de 100 mm de classe 1 (étalon de référence). Les écarts d'indication des mesures répétitives, par rapport à la valeur de référence 100, sont donnés en μm.

| N° | Mesure | Erreur Δ | E. aléatoire ΔA | E. systématique ΔS |
|---|---|---|---|---|
| Valeur no 1 | 100,0025 | 2,5 | - 0,4 | 2,9 |
| Valeur no 2 | 100,0030 | 3 | 0,1 | 2,9 |
| Valeur no 3 | 100,0035 | 3,5 | 0,6 | 2,9 |
| Valeur no 4 | 100,0030 | 3 | 0,1 | 2,9 |
| Valeur no 5 | 100,0025 | 2,5 | - 0,4 | 2,9 |
| Valeur moyenne | 100,0029 | 2,9 | 0 | 2,9 |
On remarque dans cet exemple volontairement simplifié que l'erreur systématique est constante. Elle peut être due à différentes causes (ici indicatives) : mise en place de la cale étalon sur le marbre[N 5] et/ou mauvais calibrage et jeu ou flexion du palpeur dans l'accostage pièce et/ou vitesse de déplacement programmée du palpeur trop grande…
Corrections[modifier | modifier le code]
- L'effet de la composante systématique de l'erreur peut être réduit par une correction, sans intervenir sur le système de mesurage ; dans l'exemple précédent, une correction de –2,9 μm (égale à l'erreur systématique changée de signe) sur les valeurs mesurées rapproche l'ensemble des résultats de la valeur vraie (les valeurs corrigées se trouvent entre - 0,4 et 0,6).
- l'erreur aléatoire, de par sa nature, n'est guère modifiable. Il est possible néanmoins de la minimiser en maitrisant mieux les causes d'erreurs[N 6],[9].
Approche statistique[modifier | modifier le code]
Dans le cas d'un mesurage, comportant plusieurs mesures individuelles, l'erreur de mesure est une variable aléatoire. On peut appliquer les lois de la statistique à ce mesurage[10].
La dispersion des mesures se caractérise par l'estimateur de son écart-type dit aussi écart-type expérimental
et la dispersion sur la moyenne par l'estimateur de son écart-type[N 7]
Ce qui donne pour l'exemple, présenté plus haut, de l'étalonnage partiel de la colonne
Avec un facteur d'élargissement égal à 2 (valeur communément employée en métrologie française) on aura la dispersion des mesures D et la dispersion sur l'erreur moyenne Δmoy, ceci pour 5 mesures consécutives
Ces informations statistiques n'ont que l'importance qu'on veut bien leur donner. On peut simplement souligner que plus le nombre de mesures individuelles est grand, meilleure est l'exactitude sur l'erreur de mesure ; ici, par exemple : pour la seule mesure no 1, Δ1 = 2,5 ± 0,84 µm ; pour la seule mesure no 3, Δ3 = 3,5 ± 0,84 µm ; pour les 5 mesures consécutives, Δmoy = 2,9 ± 0,38 µm.
Applications[modifier | modifier le code]
Dans le domaine grand public, quelques exemples ont été donnés dans l'introduction ; on pourrait en ajouter d'autres, actuels, comme l'erreur de mesure des thermomètres médicaux auriculaires ; l'erreur de mesure sur la distance ou la vitesse instantanée d'un compteur de vélo mal réglé ; l'erreur de localisation des GPS de voiture aux embranchements d'itinéraires…
Dans le domaine industriel, la recherche d'erreurs trouve sa place :
- en métrologie pure, dans une première approche d'une recherche d'incertitude ;
- en métrologie conventionnelle, dans la vérification des instruments de mesure suivant normes ;
- au poste de travail, dans le calibrage[N 8] de certains instruments, comme le micromètre donné en exemple plus haut ; l'erreur de mesure est généralement constatée sur une à trois mesures individuelles, au gré de l'opérateur.
-
Instructions de vérification d'un pied à coulisse.
-
Vérification d'un pied à coulisse.
Il est à remarquer qu'en production (ou dans les analyses de laboratoires), l'erreur de mesure est « transparente » dans les mesurages : la production, conjointement avec le service Qualité, fait appel à des moyens de mesure dont l'incertitude (plus rarement l'erreur) doit être connue et en rapport avec les tolérances des spécifications à respecter. C'est ce qu'on appelle la capabilité des moyens de mesure.
Prospective[modifier | modifier le code]
Les applications semblent être de plus en plus limitées dans le domaine de la vérification des instruments. En effet, l'erreur de mesure est une approche restrictive sur le doute que l'on peut avoir sur les résultats des mesures. On néglige, comme on l'a vu les erreurs liées à l'étalon et d'autres erreurs élémentaires liées aux facteurs influents de l'environnement. La recherche de l'incertitude de mesure, qui essaie de prendre en compte toutes les causes de variabilité, tend, de par sa généralisation, à supplanter la recherche d'erreur plus traditionnelle[N 9].
Erreur de mesure (ancienne version)[modifier | modifier le code]
Il faut considérer trois sources d'erreur (uncertainty en anglais) :
- l'exactitude de la mesure Δ1, ou l'incertitude (resolution en anglais) ;
- la dispersion statistique Δ2 (precision en anglais) ;
- l'erreur systématique Δ3 (accuracy en anglais).
l'erreur totale étant Δ = Δ1 + Δ2 + Δ3
Si l'on fait la comparaison avec des flèches que l'on tire sur une cible :
- la précision de mesure (resolution) désigne la taille de la pointe de la flèche ;
- la dispersion statistique (precision) désigne le fait que les flèches sont proches les unes des autres, ou bien au contraire éparpillées sur la cible ;
- l'erreur systématique (accuracy) indique si les flèches visaient bien le centre, ou bien un autre point de la cible.
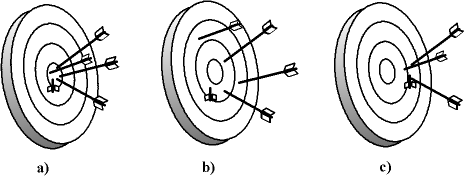
Métaphore de l'incertitude de mesure : a) la dispersion statistique et l'erreur systématique sont faibles ; b) la dispersion statistique est forte mais l'erreur systématique est faible ; c) la dispersion statistique est faible mais l'erreur systématique est forte.
Précision de mesure[modifier | modifier le code]
Le terme « précision » ne fait plus partie des termes de métrologie.
Sur un appareil analogique, la première limitation est la distance séparant les graduations ; on peut améliorer ceci avec un vernier, comme sur un pied à coulisse ou certains goniomètres, ou bien avec une vis micrométrique comme sur un palmer. Sur un appareil numérique, cette précision est donnée par le nombre de chiffres de l'affichage.
Mais il se peut que le phénomène soit instable ou bien perturbé par un phénomène extérieur aléatoire. Alors, on verra l'aiguille osciller ou bien les derniers chiffres de l'affichage numérique changer. Ceci réduit la précision de mesure, on ne peut considérer que la partie stable du nombre obtenu. Voir l'article Rapport signal sur bruit.
Lorsque l'on utilise des publications très anciennes pour évaluer un événement non reproductible (l'objet a disparu ou s'est altéré, ou bien il s'agit d'un événement unique), on doit parfois avoir recours à une échelle empirique, comme l'échelle de Mercalli ou de Rossi-Forel pour les séismes ou l'échelle de Mohs pour la dureté d'un matériau, l'évaluation de Δ1 devient alors difficile ; cela n'est possible que si l'on peut établir une correspondance avec une échelle « moderne » basée sur une mesure physique. Par exemple, on essaie d'établir une correspondance entre les dégâts d'un séisme décrits dans des écrits antiques et l'énergie des ondes sismiques.
De même, lorsque la mesure consiste à classifier un phénomène dans une catégorie (cas par exemple d'un sondage d'opinion ou du recensement des pathologies), il n'est pas possible de définir Δ1.
Dispersion statistique[modifier | modifier le code]
Si l'on mesure plusieurs fois le même phénomène avec un appareil suffisamment précis, on obtiendra chaque fois un résultat différent xi. Ceci est dû à des phénomènes perturbateurs ou, pour les mesures extrêmement précises, à la nature aléatoire du phénomène (chaos, incertitude quantique).
Parmi les phénomènes perturbateurs, on peut dénombrer :
- l'erreur d'échantillonnage : c'est lorsque l'on prélève un échantillon qui n'est pas représentatif de ce que l'on veut mesurer ; le résultat dépend alors de la manière dont on choisit l'échantillon ;
- l'erreur de préparation : c'est lorsque la préparation de l'échantillon introduit un biais ; l'échantillon s'altère pendant le transport, le stockage ou la manipulation (pollution, dégradation, transformation physique ou chimique) ;
- la stabilité de l'appareil : celui-ci peut être sensible aux variations de température, de tension d'alimentation électrique, aux vibrations, aux perturbations électromagnétiques des appareils environnants… ou bien présenter un défaut de conception ou une usure (bruit de fond électronique, pièce instable…)
Sur un grand nombre de mesures, on peut considérer que l'on a une probabilité dont la distribution est gaussienne. Le résultat de la mesure sera alors la moyenne empirique Ê des résultats
le carré de l'écart type σ2 de la gaussienne peut s'évaluer avec la variance empirique corrigée :
L'erreur due à la dispersion statistique est alors estimée par
k étant une constante dépendant du niveau de confiance, c'est-à-dire de l'erreur admissible.
En physique, on prend souvent k = 3, ce qui correspond à un intervalle de confiance de 99,73 %, c'est-à-dire que 99,73 % des valeurs xi sont comprises entre Ê - Δx et Ê + Δx et 0,27 % seront hors de cet intervalle ; sur 1 000 mesures, seules trois seront en dehors de l'intervalle. Dans de nombreux cas, on se contente de prendre k = 2, soit un niveau de confiance de 95 % (5 mesures hors intervalle pour cent mesures). Pour une entreprise ayant une production énorme, 0,27 %, et a fortiori 5 %, peuvent être encore trop.
Par exemple, imaginons qu'une entreprise produise des pièces dont la longueur ℓ doit avoir une précision Δℓ donnée ; l'outil de production, après réglage, produit des pièces avec une dispersion σ sur ℓ :
- si Δℓ = 2⋅σ, alors pour un milliard de pièces produites, 50 millions iront au rebut, ce qui est énorme ;
- si Δℓ = 3⋅σ (grâce à une optimisation de l'outil de production, l'entreprise a divisé la dispersion σ par un facteur 1,5), alors pour un milliard de pièces produites, 2,7 millions iront au rebut, ce qui est encore important ;
- si elle réussit à diminuer σ encore de moitié, on aura alors Δℓ = 6⋅σ, soit un taux de rebut de 2 × 10−9 (0,000 000 2 %), deux pièces iront au rebut par milliard produite. Ce niveau de confiance très exigeant a donné son nom à une méthode de gestion appelée Six Sigma.
Voir aussi les articles Critères de dispersion et Loi normale.
Si l'on a peu d'échantillons, il faut utiliser un coefficient plus grand pour prendre en compte l'erreur faite sur la détermination de Ê et de (voir la loi statistique de Student). On peut aussi volontairement choisir un intervalle de confiance plus grand ou plus petit, et donc prendre un coefficient plus grand ou plus petit. À titre d'exemple :
| Niveau de confiance | 5 mesures | 10 mesures | 20 mesures | > 100 mesures (loi normale) |
|---|---|---|---|---|
| 50 % | 0,73⋅σ | 0,70⋅σ | 0,69⋅σ | 0,67⋅σ |
| 68 % | 1⋅σ | |||
| 70 % | 1,16⋅σ | 1,09⋅σ | 1,06⋅σ | 1,04⋅σ |
| 87 % | 1,5⋅σ | |||
| 90 % | 2,02⋅σ | 1,81⋅σ | 1,73⋅σ | 1,65⋅σ |
| 95 % | 2,57⋅σ | 2,23⋅σ | 2,09⋅σ | 1,96⋅σ |
| 99 % | 4,03⋅σ | 3,17⋅σ | 2,85⋅σ | 2,56⋅σ |
| 99,7 % | 3⋅σ | |||
| 99,9 % | 6,87⋅σ | 4,59⋅σ | 3,85⋅σ | 3,28⋅σ |
| 99,999 999 8 % | 6⋅σ |
Sur une gaussienne, la largeur à mi-hauteur (full width at half maximum, FWHM) représente un intervalle de confiance d'environ 76 % (soit 3/4) pour un grand nombre de mesures.
Dans le cas de mesures physiques ou chimiques, l'évaluation de la dispersion statistique se fait par des mesures de répétabilité et de reproductibilité, et éventuellement par des mesures croisées inter-laboratoires :
- répétabilité : un même opérateur effectue plusieurs fois la même mesure, et l'on relève les résultats ; ceci permet d'évaluer la stabilité dans le temps de l'appareil et de l'échantillon (vieillissement dans l'appareil ou hors de l'appareil) ; dans le cas d'une analyse chimique, on mesure plusieurs fois le même échantillon ;
- reproductibilité : on mesure plusieurs fois le même matériau ou phénomène ; la différence avec la répétabilité est que l'on reprépare à chaque fois la mesure (par exemple prélèvement de l'échantillon et conditionnement pour la mesure, ou bien mise en place de l'appareil de mesure et réglage préalable) et que ceci est fait par différentes personnes ; ceci permet de prendre en compte la totalité de la chaîne de mesure et les erreurs humaines ;
- essais croisés interlaboratoires, ou essais circulaires : un échantillon inconnu est envoyé à plusieurs laboratoires et l'on compare les résultats, on prend ainsi en compte la diversité des appareils de mesure et les habitudes de travail.
Si la précision de mesure est inférieure à la dispersion statistique, on mesure alors toujours le même résultat (aux erreurs de lecture ou d'utilisation près), cf. infra.
Note : Dans le cas d'un phénomène aléatoire (processus stochastique, cas par exemple du sondage d'opinion), on ne cherche pas à connaître une valeur et une erreur, mais à connaître la répartition statistique des valeurs. Voir aussi Loi des grands nombres.
Propagation de l'erreur[modifier | modifier le code]
Le résultat d'une mesure est fréquemment utilisé pour faire des calculs. Par exemple, dans le cas d'un radar routier (cinémomètre) on mesure un décalage de fréquence et ce décalage est utilisé pour calculer la vitesse du véhicule, avec la loi de Doppler-Fizeau. Il faut donc, à partir de l'erreur commise sur la mesure du décalage de fréquence, estimer l'erreur sur la vitesse.
D'une manière générale, on mesure une valeur x, et l'on calcule une valeur y = ƒ(x) ; on veut estimer Δy à partir de Δx.
Erreur et test d'acceptation[modifier | modifier le code]
La mesure sert fréquemment dans les tests d'acceptation, c'est-à-dire que la valeur mesurée détermine si l'objet répond bien aux critères imposés. Cette notion est assez large :
- en médecine, cela permet de poser un diagnostic (éliminer ou confirmer une maladie) ;
- dans la fabrication, cela permet de dire si le lot de matière première peut être utilisée, ou si le produit fabriqué est conforme au cahier des charges ;
- en docimologie, cela permet de délivrer un diplôme, une certification ;
- pour un appareil de mesure : à déterminer si
- la méthode convient à l'usage (peut-on utiliser telle méthode pour mesurer tel paramètre dans telles conditions avec telle précision ?),
- le modèle d'appareil convient à l'usage (choix d'un fournisseur, choix dans la gamme d'un fournisseur),
- l'appareil livré et installé correspond aux spécifications,
- le manipulateur, le laboratoire utilise une procédure fiable (préparation, manipulation…).
On estime en général qu'une méthode ne peut être utilisée que si la dispersion statistique est au moins 5 ou 10 fois inférieure à la valeur limite.
Exemple :
- si pour un métier on n'accepte que les personnes mesurant au moins 1,60 m, il faut une méthode de mesure ayant une dispersion statistique inférieure à 16 cm ;
- si la teneur en soufre dans une essence doit être inférieure à 150 ppm en masse, il faut une méthode de mesure ayant une dispersion statistique inférieure à 15 ppm.
De manière générale, la fourchette de valeurs d'admissibilité doit prendre en compte l'erreur globale. Le sens de la prise en compte de l'erreur globale dépend du type de risque que l'on veut éviter :
- si l'on veut éviter les faux positifs (c'est-à-dire accepter un produit alors qu'il est inacceptable), on resserre la fourchette ;
- si l'on veut éviter les faux négatifs (c'est-à-dire rejeter un produit valable), alors on élargit la fourchette.
Pour tester un appareil ou une procédure, on vérifie que les tests de répétabilité et de reproductibilité sont compatibles avec la précision visée ; pour tester une méthode de mesure, on vérifie que les essais interlaboratoires (ou circulaires) sont compatibles avec la précision visée (cf. supra).
Utilisation de calculatrices[modifier | modifier le code]
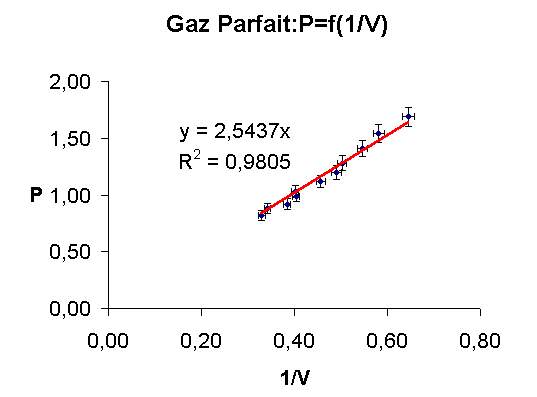
Ce qui vient d'être fait peut-être fait par calcul direct avec une calculatrice ou un tableur (sur ordinateur), par l’utilisation de graphes et de barres d'erreurs
Reprenons l'exemple de l'étude des gaz parfaits. Si l'on trace P en fonction de 1/V, on obtiendra théoriquement une droite passant par l'origine , avec comme pente , soit , n et T étant maintenus constants (l'enceinte ou cellule de mesure contenant le gaz étant sans fuite et thermostatée avec T connu à 0,2 %), P étant mesuré, en utilisant un manomètre, avec 5 % d'erreur relative, et V étant mesuré avec 2 % d'erreur relative, pour chaque point de mesure expérimentale (P,1/V), on trace des barres d'erreurs représentant l'erreur absolue.
Un programme de « fit » ou d'ajustage de courbe, basé sur l'idée de minorer la distance de la droite (ou courbe) à tous les points expérimentaux, permet de tracer la droite théorique et de calculer sa pente nRT avec un coefficient de confiance r2 proche de l'unité, si le fit est bon.
On utilise la méthode des moindres carrés : le programme utilisé somme les distances élevées au carré entre la droite et chaque point, le minimum de cette somme correspondant à la meilleure droite de régression.
Dans le cas de figure ci-dessus, on obtient ainsi nRT= 2,54 (1,00 ± 0,07) Joule
Ceci permet de dire qu'à n et T constants, l'expérience confirme que PV est constant à 7 % près pour le gaz étudié et que pour améliorer ce résultat, il faut mesurer P à mieux que 5 % ou V à mieux que 2 %.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Le dictionnaire indique « erreur absolue » pour « erreur de mesure » ; l'erreur absolue, dont le terme « absolu » prête à confusion, n'est plus d'usage en métrologie.
- Il suffit de taper « erreur de mesure » sur un moteur de recherche pour s'en convaincre.
- Si l'incertitude de mesure de l'étalon n'est pas négligeable, il faut passer par le concept d'incertitude.
- la cale est de classe 2, avec une incertitude < ± 0,06 µm négligeable ici.
- Si la cale est simplement posée sur le marbre, il peut y avoir une différence, sensiblement constante, voisinant le centième de mm, par rapport à une cale « forcée à adhérer » sur la référence, comme doivent le faire les métrologues
- Voir Incertitude de mesure
- Les notions de statistique sur les dispersions sont supposées connues ; voir Critères de dispersion
- Un calibrage consiste à corriger l'erreur systématique. Ce terme disparu du VIM 2008, est encore en usage. Le terme correct est « ajustage », parfois aussi appelé réglage.
- On remarquera que les documents industriels de vérification, ci-dessus, comportent des déterminations traditionnelles d'erreurs mais aussi des recherches d'incertitudes simplifiées adaptées aux contraintes de la production.
Références[modifier | modifier le code]
- Citation corrigée extraite du dictionnaire : Le petit Larousse compact, .
- Voir le VIM (référencé en bibliographie) dans l'édition 1993 (3.10). Dans le VIM 2008, le terme a disparu.
- VIM collectif 2008 ; il existe une version plus actuelle du VIM, de 2012, avec de petites corrections, mais moins facile d'exploitation.
- VIM collectif 2008, p. 22, n° 2.16. ; la définition de l'édition 1993 était « Résultat d'un mesurage moins une valeur vraie du mesurande »
- M. Collinet CNAM 1995, p. 2
- VIM collectif 2008, p. 23 ; n° 2.19.
- VIM collectif 2008, p. 22 n° 2.17.
- VIM collectif 2008, p. 23 ; n° 2.18.
- D'après M. Collinet CNAM 1995, p. 4
- Collectif AFNOR 1996, p. 149-173.
Annexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
 (en + fr) VIM collectif, JCGM 200 : 2008 : Vocabulaire international de métrologie - Concepts fondamentaux et généraux et termes associés, BIPM, (lire en ligne).
(en + fr) VIM collectif, JCGM 200 : 2008 : Vocabulaire international de métrologie - Concepts fondamentaux et généraux et termes associés, BIPM, (lire en ligne). M. Collinet CNAM, Expression des incertitudes de mesures, Senlis, CETIM, .
M. Collinet CNAM, Expression des incertitudes de mesures, Senlis, CETIM, . Collectif AFNOR, Métrologie dans l'entreprise : Outil de la qualité, Paris, AFNOR, , 310 p. (ISBN 2-12-460701-4).
Collectif AFNOR, Métrologie dans l'entreprise : Outil de la qualité, Paris, AFNOR, , 310 p. (ISBN 2-12-460701-4).- Collectif CNDP, La mesure : Actes des 7es entretiens de la Villette, Paris, CNDP, .
Articles connexes[modifier | modifier le code]
- Incertitude de mesure
- Métrologie
- Critères de dispersion
- Qualité métrologique des appareils de mesure
- Écart type