Coloriage des routes

Un graphe orienté avec un coloriage synchronisant.

Le coloriage des routes est un problème combinatoire qui relève à la fois de la théorie des graphes et en théorie des automates. Il s'agit d'une propriété de synchronisation dans un réseau routier. La question est de savoir si l'on peut « colorier » les routes d'un réseau routier (ou, de manière équivalente, colorier les arcs d'un graphe fini) de telle sorte que, quel que soit le point de départ, en suivant la séquence de routes de même nom (ou de même couleur), on arrive au même point d'arrivée. Le problème du coloriage des routes et la conjecture correspondante (la conjecture du coloriage des routes) ont d'abord été formulés par Adler et Weiss en 1970. Le théorème correspondant, le théorème du coloriage des routes, a été démontré par Avraham Trahtman en 2009.

Exemple

L'image à droite montre un graphe orienté avec huit sommets, où chaque sommet a degré sortant 2. Dans cet exemple, les sommets ont aussi degré entrant 2, mais ceci n'a pas d'influence sur la suite. Les arcs sont colorés en bleu (B) ou en rouge (R). La propriété de synchronisation dit que, si on suit des arcs d'une séquence fixe de couleurs, alors on arrive toujours au même sommet, quel que soit le point de départ. Ainsi :

• en suivant dans l'ordre les neuf arcs du chemin de couleurs « B R R B R R B R R », on arrive au sommet jaune, et ceci quel que soit le sommet de départ.
• de même, en suivant dans l'ordre les neuf arcs du chemin de couleurs « B B R B B R B B R », on arrive au sommet vert, quel que soit le sommet de départ.

Le théorème du coloriage affirme que, pour une certaine catégorie de graphes, il est toujours possible de créer un coloriage avec cette propriété.

Description formelle

Soit $G$ un graphe orienté fortement connexe fini, dont tous les sommets ont même degré sortant $k$. Soit $A$ un alphabet à $k$ lettres. Un coloriage synchronisant (aussi connu sous le terme collapsible coloring en anglais) de $G$' est un étiquetage des arcs de $G$ avec les lettres de $A$ tel que

1. chaque sommet possède exactement un arc sortant portant une lettre donnée et que,
2. pour chaque sommet $s$ du graphe, il existe un mot $w$ sur $A$ tel que tous les chemins de $G$ étiquetés par $w$ mènent à $s$.

La terminologie de coloriage synchronisant est due à la relation entre cette notion et celle de mot synchronisant dans la théorie des automates finis : Le graphe avec son étiquetage est le graphe d'un automate fini déterministe complet. La condition de synchronisation se traduit par l'existence d'un mot $w\in A^{*}$ tel que $q\cdot w=s$ pour tout sommet $q$ de $G$. Un tel mot est dit synchronisant.

Pour qu'un tel coloriage puisse exister, une condition nécessaire est que le graphe $G$ est apériodique (en). Le théorème du coloriage énonce que cette apériodicité est aussi une condition suffisante pour l'existence d'un tel coloriage :

Théorème — Tout graphe orienté fini, apériodique, fortement connexe et dont tous les sommets ont même degré sortant possède un coloriage synchronisant.

Relation avec les automates

Synchronisation

Le graphe avec son étiquetage est le graphe d'un automate fini déterministe complet sur l'alphabet $A$ des couleurs. Une suite de couleurs est un mot $w\in A^{*}$, et l'existence d'un mot synchronisant revient à l'existence d'un mot $w\in A^{*}$ tel que $q\cdot w=s$ pour un sommet $s$ et tout sommet $q$ de $G$. Il est commode d'utiliser la notation que voici : pour un ensemble $P$ de sommets et un mot $w$, on note $P\cdot w=\{p\cdot w\mid p\in P\}$ ; c'est l'ensemble des sommets atteints à partir d'un somme de $P$ par un chemin étiqueté par $w$. Un mot synchronisant est un mot $w$ tel que $Q\cdot w$ est un singleton. On appelle rang d'un mot $w$ le nombre d'éléments de $Q\cdot w$. Un mot synchronisant est donc un mot de rang 1. Un automate qui possède un mot synchronisant est dit lui-même synchronisant ou aussi synchronisé.

Jetons

Automate de départ.

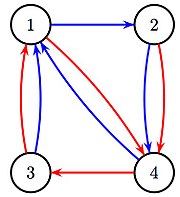
Le calcul des rangs s'illustre bien par un jeu à jetons. Au départ, chaque état contient un jeton. À l'application d'une lettre R ou B, les jetons se déplacent d'un état au suivant selon la couleur. Après une séquence de lettres $w$, chaque état contient des jetons dont le nombre est le nombre d'états qui sont envoyés sur cet état par $w$. Le fait qu'à la fin tous les jetons se trouvent dans un même état exprime précisément que le mot employé est synchronisant.

Au départ, chaque état contient un jeton. La lettre B donne la deuxième distribution, la lettre R la troisième, enfin B la dernière : le mot BRB est synchronisant.

Preuves

Avant la démonstration de Trahtman en 2009, des cas particuliers ont été prouvés, notamment par O'Brien et par Jarkko Kari.

Un cas simple

Dans un cas particulier, un argument simple donne une démonstration simple : c'est le cas où il y a une boucle autour d’un sommet dans le graphe. Soit $r$ un tel sommet. Comme le graphe est fortement connexe, il existe un arbre recouvrant, enraciné en $r$, avec tous les arcs dirigés vers $r$. Il suffit de colorer les arcs de cet arbre par la même couleur R pour obtenir un coloriage synchronisant : la suite de $n$ arcs R, où $n$ est le nombre de sommets, mène de tout sommet à $r$. Cette idée simple devient, plus élaborée, une des bases de la démonstration donnée par Trahtman.

Une extension de ce cas est le résultat de O'Brian : si le graphe est sans arcs multiples et a un circuit dont la longueur est un nombre premier, alors il possède un coloriage synchronisant avec toutes les flèches de ce circuit de même couleur.

Paire stable

Culik, Karhumäki et Kari ont défini une opération de réduction qui permet, dans certains cas, de démontrer le résultat par récurrence ; c'est la notion de paire stable.

Deux états $s$ et $t$ forment une paire stable si, pour tout mot $x$, il existe un mot $y$ tel que le produit $xy$ mène $s$ et $t$ dans le même état. Dans un automate synchronisant, toute paire d’états est stable. Si $(s,t)$ est une paire stable, alors toute paire $(s\cdot w,t\cdot w)$ est stable ; de plus, si $(s,t)$ et $(t,r)$ sont deux paires stables, alors $(s,r)$ est une paire stable : la relation $s\equiv t$ si $(s,t)$ est donc une relation d’équivalence, et de fait une congruence (si $s\equiv t$ alors $s\cdot x\equiv t\cdot x$). L'énoncé est :

Čulik, Karhumäki et Kari — Si l’automate obtenu en fusionnant les paires stables possède un coloriage synchronisant, alors l’automate de départ en possède un également.

Un corollaire est de Kari :

Kari —  Un graphe eulérien orienté possède un coloriage synchronisant.

Si l’automate obtenu en fusionnant les paires stables possède un coloriage synchronisant, alors l’automate de départ en possède un également.

Preuve de Trahtman (esquisse)

La preuve de Trahtman est constructive et donne un algorithme qui permet de synchroniser le graphe en temps polynomial. L’algorithme de Trahtman est cubique en la taille du graphe. L’algorithme peut être vu comme suit : on cherche une paire stable de sommets $(s,t)$, on fusionne la paire, on cherche un coloriage synchronisant du graphe plus petit obtenu, puis on remonte le coloriage au graphe de départ : si dans le graphe de départ, il y a une flèche $(s,c,t)$ et pas d’arc $({\bar {s}},c,{\bar {t}})$ dans le quotient, il existe un arc $({\bar {s}},d,{\bar {t}})$ dans le graphe quotient pour une couleur $d\neq c$ ; on échange les couleurs $c$ et $d$ des arcs partant de $s$.

Pour trouver une paire stable, on considère le graphe composé des arcs d’une couleur fixée R. C’est un graphe fonctionnel, avec un arc et un seul sortant de chaque sommet. Chaque composante connexe, appelée un amas (en anglais cluster), est formée d’un circuit et d’un ensemble d’arborescences greffées sur ce circuit. Le niveau d’un sommet est sa distance à un sommet du circuit. Un sommet maximal est un sommet de niveau maximal. C'est une feuille d'une arborescences (sauf si tous les sommets sont de niveau 0).

L'observation cruciale de Trahtman est la suivante :

Si tous les sommets maximaux appartiennent à une même arborescence, alors le graphe possède une paire stable. Soit $r$ la racine ce cette arborescence. Cette paire est composée du sommet précédent $r$ dans le circuit de l’amas, et du sommet précédent $r$ dans l’arborescence, sur le chemin du sommet maximal vers $r$.

Les sommets $p$ et $q$ sont maximaux, le sommet $s$ ne l'est pas.

La preuve du théorème se poursuit par une série d'échanges (flips en anglais) qui consistent à échanger les couleurs des arcs sortant d'un sommet pour raccourcir ou briser les circuits et pour diminuer les niveaux des sommets.

Développements

Trahtman a présenté en 2010 un algorithme au colloque CSR ; Marie-Pierre Béal et Dominique Perrin ont décrit un algorithme en temps quadratique pour trouver un coloriage synchronisant. Les relations avec la conjecture de Cerny sur la longueur d'un mot synchronisant sont détaillés dans le chapitre de Béal et Perrin du livre Combinatorics, automata and number theory

Articles connexes

• Théorème des quatre couleurs
• Coloration de graphe
• mot synchronisant

Notes

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Road coloring theorem » (voir la liste des auteurs).

Références

Articles

• [1970] Roy L. Adler et Benjamen Weiss, Similarity of automorphisms of the torus, coll. « Memoires of the American Mathematical Society » (n^o 98), 1970, ii+48 (ISBN 978-1-4704-0048-4, MR 0257315).

• [1981] G. L. O'Brien, « The road-colouring problem », Israel Journal of Mathematics, vol. 39, n^os 1–2,‎ 1981, p. 145–154 (DOI 10.1007/BF02762860).

• [2003] Jarkko Kari, « Synchronizing finite automata on Eulerian digraphs », Theoretical Computer Science, vol. 295, n^os 1-3,‎ 2003, p. 223–232 (DOI 10.1016/S0304-3975(02)00405-X).

• [2005] Rajneesh Hegde et Kamal Jain, « A min-max theorem about the road coloring conjecture », Discrete Mathematics & Theoretical Computer Science (Proc. EuroComb 2005),‎ 2005, p. 279–284 (lire en ligne).

• [2002] Karel Čulik, Juhani Karhumäki et Jarkko Kari, « A note on synchronized automata and road coloring problem », dans Developments in Language Theory (Vienne 2001), Springer, coll. « Lecture Notes in Computer Science » (n^o 2295), 2002 (DOI 10.1007/3-540-46011-X_14), p. 175-185.

• [2009] Avraham N. Trahtman, « The road coloring problem », Israel Journal of Mathematics, vol. 172, n^o 1,‎ 2009, p. 51–60 (DOI 10.1007/s11856-009-0062-5, arXiv 0709.0099).

• [2010] Avraham N. Trahtman, « A Partially Synchronizing Coloring », dans F. Ablayev et E. W. Mayr (éditeurs), Computer Science – Theory and Applications. CSR 2010, Springer, coll. « Lecture Notes in Computer Science » (n^o 6072), 2010 (ISSN 0302-9743, DOI 10.1007/978-3-642-13182-0_36), p. 362–370.

• [2014] Marie-Pierre Béal et Dominique Perrin, « A quadratic algorithm for road coloring », Discrete Applied Mathematics, vol. 169,‎ 2014, p. 15-29 (ISSN 0166-218X, DOI 10.1016/j.dam.2013.12.002, HAL hal-00627821v2).

• [2016] Marie-Pierre Béal et Dominique Perrin, chap. 7 « Synchronised automata », dans Valérie Berthé et Michel Rigo (éditeurs), Combinatorics, Words and Symbolic Dynamics, Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications » (n^o 135), 2016 (ISBN 978-0-521-51597-9, 9781139924733 et 9781107077027, DOI 10.1017/cbo9781139924733.008, présentation en ligne), p. 213-240.

• [2023] Sophie MacDonald, « The road problem and homomorphisms of directed graphs », Theoretical Computer Science, vol. 968,‎ 11 août 2023, article n^o 113981 (25 pages) (DOI 10.1016/j.tcs.2023.113981, arXiv 2201.12942).

Présentations

• [2009] Dominique Perrin, « Le coloriage des routes », Université Paris-Est-Marne-la-Vallée, 17 décembre 2009 (consulté le 23 décembre 2017).
• [2012] Marie-Pierre Béal et Dominique Perrin, « Road coloring », CANT 2012, Université Paris-Est-Marne-la-Vallée, 2012 (consulté le 23 décembre 2017).