Boucle à phase asservie
Une boucle à phase asservie, ou boucle à verrouillage de phase ou BVP[1] (en anglais, phase-locked loop, ou PLL), est un montage électronique permettant d'asservir la phase ou la fréquence de sortie d'un système sur la phase ou la fréquence du signal d'entrée. Elle peut aussi asservir une fréquence de sortie sur un multiple de la fréquence d'entrée.
Histoire[modifier | modifier le code]
L'invention de la boucle à verrouillage de phase est attribuée à un ingénieur français, Henri de Bellescize, en 1932.
Étant donné que la réalisation des circuits correspondants est assez complexe et demande plusieurs dizaines de composants, ce n’est que dans les années 1960, avec l'apparition des circuits intégrés que la mise en œuvre de l'invention s'étend de façon considérable.
Descriptif de la boucle à verrouillage de phase (PLL)[modifier | modifier le code]
Structure[modifier | modifier le code]
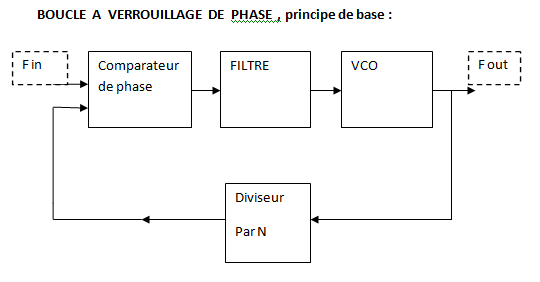
Une boucle à verrouillage de phase classique est constituée :
- d'un comparateur de phase (Phase Frequency Detector - PFD) ;
- d'un filtre de boucle ;
- d'un oscillateur commandé en tension (Voltage Controlled Oscillator - VCO) et
- d'un diviseur de fréquence éventuel.
On la trouve également sous la forme d'un circuit intégré.
Schéma du système[modifier | modifier le code]
Relation entre fréquence d'entrée et fréquence de sortie :
Principe de fonctionnement[modifier | modifier le code]
Le comparateur de phase donne un signal fonction de l'écart de phase entre ses deux signaux d'entrée. Après passage par le filtre de boucle, le signal est appliqué à l'oscillateur commandé par une tension, le VCO.
Le signal de sortie du VCO est appliqué (après éventuellement une division par N de sa fréquence) sur l'entrée du comparateur de phase. On constitue ainsi un système bouclé qui asservit la fréquence ou la phase du VCO sur celles du signal d'entrée Fin.
Une boucle PLL peut avoir différentes fonctions.
FONCTION DÉMODULATEUR DE PHASE OU DE FRÉQUENCE :
N = 1 . La bande passante du filtre de boucle est supérieure aux fréquences de modulation, donc le VCO reçoit une tension qui va lui permettre de suivre les variations rapides , c'est-à-dire la modulation. Le signal de modulation est disponible en sortie du filtre de boucle.
FONCTION RÉCUPÉRATION DE PORTEUSE :
N = 1 . La bande passante du filtre est basse et le filtre ne transmet pas la modulation . La fréquence du VCO ne suit que les variations lentes de fréquences. On dispose ainsi en sortie du VCO d'un signal RF non modulé dont la fréquence est la fréquence moyenne du signal d'entrée.
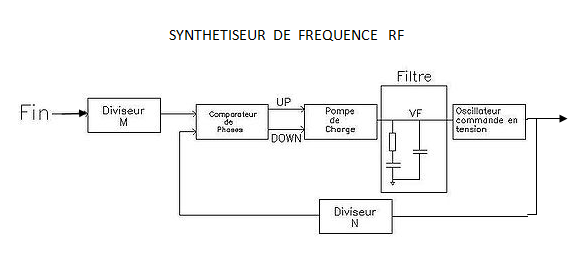
FONCTION SYNTHÈSE DE FRÉQUENCE :
La fréquence Fin est donnée par un quartz . Après division par un nombre prédéterminé M , on obtient le "pas" qui représente les sauts de fréquence possibles par programmation.
La fréquence de sortie du VCO est divisée par un nombre N en général programmable, afin de donner aussi une fréquence égale au "pas". En mode établi, la sortie du diviseur est égale au "pas" , donc la fréquence du VCO est égale à N fois le "pas".
Si la fréquence du VCO n'est pas égale à la fréquence programmée, alors le VCO va recevoir du filtre un signal de correction afin de l'amener sur la fréquence prévue.
Détermination du filtre et fonction de transfert[modifier | modifier le code]
Comme tous les systèmes asservis, la stabilité de la boucle de phase va dépendre de la fonction de transfert en boucle ouverte[2].
Différents filtres et fonctions de transfert sont possibles.
Pour déterminer le filtre, nous allons utiliser la méthode du diagramme de Bode, qui a l'avantage de nécessiter peu de calculs et de montrer ce qui se passe.
Pour étudier cette stabilité, il est nécessaire de définir certains termes :
: pente du VCO en radians par volt. Si le VCO a une pente (en hertz par volt), alors .
: sensibilité de sortie du comparateur de phase, en volts par radian. Par exemple, avec un comparateur de phase du type CMOS "tristate" comme le CD 4046, on a .
: rang de division de la sortie du VCO.
: Pulsation théorique à laquelle la boucle ouverte sans filtre coupe l'axe 0 dB (gain unité)[3]. On a . Ce paramètre dépend du comparateur de phase et du VCO, il est donc en général prédéterminé. il est important de le connaître avant de décider du filtre qui sera placé derrière le comparateur de phase.
La boucle sera stable si la courbe de réponse en boucle ouverte est moins pentue que -12dB/octave au point où la courbe coupe l'axe horizontal 0 dB du diagramme de Bode. (Cette condition de pente est équivalente à la condition : phase supérieure à -180° Critère de Revers.)
- Premier cas, si le filtre rajouté ne présente pas de fréquence de coupure en dessous de , la boucle sera inconditionnellement stable, car dans ce cas, la courbe de réponse en boucle ouverte a une pente de l'ordre de −6 dB par octave jusqu'à .
C'est le cas de figure des boucles PLL pour les démodulateurs, et pour les cas où le bruit généré par le comparateur n'a pas une importance essentielle . C'est la courbe en noir sur le diagramme de Bode ci-dessous.
- Deuxième cas, si le filtre rajouté présente une fréquence de coupure en dessous de , la boucle peut être instable. C'est généralement le cas des synthétiseurs de radio fréquences, et des boucles très lentes de récupération de la porteuse.
Nous devons dans ce cas considérer avec soin la courbe en boucle ouverte.
Supposons donc que le comparateur de phase est suivi d'un filtre passe bas du premier ordre, de pulsation de coupure , inférieure à .
La boucle ouverte est alors un système du second ordre. Au delà de le diagramme de Bode montre une pente qui se rapproche des 12 dB par octave.
Pour avoir un système stable, il faut que la pente de la courbe n'atteigne pas −12 dB par octave au point où la courbe coupe l'axe horizontal "0 dB".
On crée pour cela un deuxième coude dans la fonction de transfert, à la pulsation , pour "redresser" la courbe et la ramener à une pente nettement plus faible que −12 dB par octave au point où la courbe coupe l'axe 0 dB.
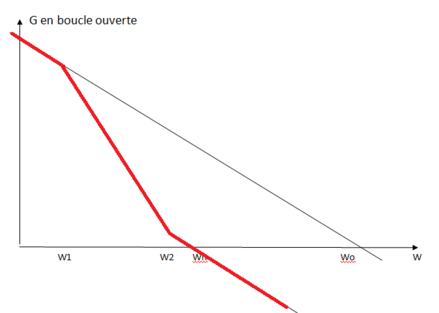
En tenant compte du filtre avec et , la pulsation à laquelle la boucle ouverte a un gain de 0 dB est nommée , c'est la "pulsation naturelle de la boucle".
La stabilité peut s'évaluer par le facteur d'amortissement : On considère que le verrouillage s'effectue le plus rapidement possible pour = 0,7. Dans ce cas, on a une montée stable de la tension de sortie du filtre , comme le montre l'image plus bas.
Les valeurs plus faibles de induisent des sur-oscillations importantes, voire permanentes, et pour les valeurs de plus grandes que 1, il n'y a plus de sur-oscillations, mais l'état stationnaire est atteint plus lentement.
La stabilité peut aussi s'évaluer par la marge de phase : à la pulsation , c'est l'écart de phase par rapport à la phase qui entraînerait une instabilité.
Réduction du bruit : On rajoute en général derrière le filtrage cité ci-dessus une autre cellule qui coupe à une fréquence . Cette fréquence doit être au moins 7 fois supérieure à pour ne pas réduire la stabilité obtenue précédemment.
EXEMPLE DE CONSTITUTION DU FILTRE DE BOUCLE EN SORTIE D'UN COMPARATEUR "TRISTATE"

On a calculé précédemment .
Le filtre ci-contre est constitué de , et .
En pratique on se donne au départ en tenant compte des critères suivants.
Plus sera grand, plus le verrouillage sera rapide. En contrepartie, le filtrage des résidus et bruits issus du comparateur de phase sera mauvais.
On optera en général pour un assez inférieur à pour cette raison.
Connaissant et , on en déduira et on en déduit alors et sachant que les résistances font quelques milliers d'ohms.
Le calcul de se fera après avoir choisi le coefficient d'amortissement .
On choisira compris entre 0,7 et 1 ; on a alors .
Remarque : en général on trouve que est deux à trois fois plus petite que .
Rajout d'une coupure à :
Afin de réduire encore le bruit, on a intérêt à rajouter une nouvelle coupure à .
Un condensateur sera placé en parallèle sur la sortie du filtre.
Donc la valeur de sera de l'ordre de .
Pour ne pas nuire à la stabilité, on prendra en pratique bien supérieur à , par exemple .



Verrouillage[modifier | modifier le code]
Le détecteur ou comparateur de phase doit fournir, après filtrage, une tension continue (ou lentement variable) proportionnelle à l'écart de phase existant entre les signaux d'entrée .
On distingue les comparateurs linéaires classiques, qui donnent en sortie un signal proportionnel à la différence de phase entre les signaux d'entrée . Pour ces détecteurs, si on applique en entrée deux signaux de fréquences différentes, on obtient en sortie un signal en dent de scie .Si les deux signaux d'entrée sont éloignés en fréquence (cas du VCO loin de sa fréquence désirée) alors le signal de sortie est une dent de scie de fréquence assez élevée (différence des fréquences entre les entrées) et après filtrage passe bas, on n'aura pas forcément la tension nécessaire pour "verrouiller" la boucle. Donc le système ne pourra se verrouiller sur la fréquence programmée que si la fréquence de départ du VCO n'est pas trop éloignée de la fréquence désirée.
Dans les années 1970 sont apparus des détecteurs dits "tristate" dits aussi séquentiels, comme le CD 4046 dont la sortie est très différente. La sortie est constituée par l'ouverture de portes, soit vers le +, soit vers le -, et de largeur dépendant de la différence de phase. Lorsque les signaux d'entrée sont en phase, la sortie est à l'état haute impédance. Par ailleurs, lorsque les signaux d'entrée ont des fréquences différentes, la sortie est fermée vers le + ou fermée vers le -. Il s'agit donc aussi d'un comparateur de fréquence. Cette amélioration est importante par rapport aux comparateurs classiques : Avec un tristate et sa "pompe de charge", si la fréquence du VCO est loin de la fréquence désirée, le signal de sortie reste à l'état haut ou à l'état bas en permanence, selon que la fréquence sur une entrée est supérieure ou inférieure à celle de l'autre entrée. On n'a donc pas de problème de verrouillage .
Oscillateur commandé en tension[modifier | modifier le code]
ou aussi OCT (en anglais : Voltage Controlled Oscillator iu VCO).
Il a pour fonction de générer un signal périodique dont la fréquence est fonction de la tension appliquée sur son entrée.
Applications[modifier | modifier le code]
Démoduler un signal radio-fréquence[modifier | modifier le code]
Dans les récepteurs radio-fréquence, un signal électromagnétique modulé suivant un schéma de modulation particulier (FSK, GMSK, QAM64...) génère une force électromotrice dans l'antenne de réception, qui est convertie en un signal électrique amplifié et filtré. Ce système utilise notamment une fréquence de référence appelée aussi fréquence de l'oscillateur local (en anglais : local oscillator), qui est générée par une boucle à verrouillage de phase.
Retrouver la fréquence porteuse d'un signal[modifier | modifier le code]
C'est le cas par exemple dans le cadre de la démodulation radio FM ou AM. Un poste radio contient une PLL dont on fait varier le filtrage du signal d'entrée. Ce signal filtré pilote ensuite la PLL, qui se cale sur cette fréquence durant ce que l'on appelle la phase d'accrochage, et génère ensuite en sortie le signal démodulé.
Multiplier une fréquence d'horloge[modifier | modifier le code]
Souvent les systèmes numériques requièrent une fréquence interne de travail importante, de l'ordre de plusieurs centaines de mégahertz. En général un cristal oscillateur piézoélectrique sert de référence car il génère une gigue d'horloge très faible. L'inconvénient du cristal est que souvent sa fréquence est basse, de l'ordre de 20 MHz à 30 MHz, et qu'il est nécessaire de multiplier sa fréquence par un facteur afin de générer l'horloge du système numérique. C'est le rôle de la PLL.
Gigue[modifier | modifier le code]
Sources de bruit[modifier | modifier le code]
Le signal d'entrée présente un certain facteur de qualité en termes de bruit caractérisé par une gigue temporelle ou par un bruit de phase. Par exemple, si la fréquence d'entrée provient d'une horloge de sortie venant d'un autre système, il contient un bruit qui va être filtré ou amplifié par la PLL, selon que la boucle le transmettra ou non au VCO. Il est donc nécessaire de bien comprendre le gabarit en bruit du signal d'entrée afin d'assurer une certaine qualité du signal de sortie du VCO. Les meilleures sources d'horloge de référence d'entrée sont les quartz oscillateurs et servent en général pour les PLL qui requièrent un minimum de qualité en entrée.
Pour la plupart des applications, les caractéristiques de bruit de phase des quartz sont très supérieures aux qualités de bruit de phase intrinsèque des VCO. Le système PLL améliore donc le bruit de phase du signal de sortie du VCO. Si la fréquence de sortie du VCO est , alors le bruit de phase de celui-ci sera amélioré autour de , dans une bande limitée par la valeur de .
Les sources de bruit intrinsèques sont liées aux éléments de la PLL, que ce soient les résistances ou les transistors. Les différents bruits à prendre en compte sont le bruit thermique, le « bruit flicker », le bruit grenaille, le bruit en créneaux... L'étude de ces bruits intrinsèques se fait de la manière suivante :
- On élabore un modèle linéaire de la PLL que l'on implémente sous un simulateur, par exemple SPICE ;
- on simule le bruit de phase de chaque sous-bloc ;
- on implémente ces bruits de phase dans le modèle linéaire de la PLL, pour en extraire en sortie le bruit de phase total de la structure.
Le filtre entre le comparateur de phase et le VCO aura donc pour tâche de filtrer ces bruits.
Dans le cas de VCO radio fréquence, les seuls bruits qui ne pourront être filtrés seront :
- le bruit de phase intrinsèque au VCO, quand on s'écarte de la porteuse de plus de ,
- si la pente est de plusieurs dizaines de MHz/volt, le bruit thermique de la résistance qui commande les diodes à capacité variable.
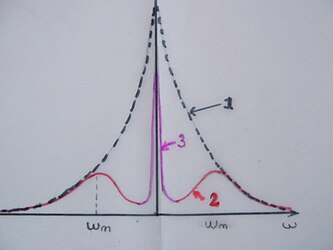
En résumé, dans la zone du spectre de + ou - autour de la porteuse, la boucle de phase :
a) réduit le bruit de phase du VCO : La courbe 1 en pointillé de l'image ci-dessous montre le spectre de la sortie du VCO non verrouillé.
La courbe 2 en rouge montre le bruit de phase du VCO verrouillé par la boucle.
b) rajoute le bruit de phase de la référence : c'est la courbe 3. (La référence possède un bruit de phase faible.)
Parasites intrinsèques[modifier | modifier le code]
Les impuretés relèvent du domaine de tout processus non stochastique (aléatoire) qui se rajoutent au signal voulu.
Une PLL consomme un courant qui présente des pics en courant qui, par l'intermédiaire des chutes de tension sur silicium ou sur la plaque de test, se traduisent par des pics de tension sur les alimentations de la PLL. Ces pics de tension génèrent alors une dégradation de la qualité du signal de sortie et ces impuretés peuvent facilement être observées en temporel sur les alimentations à l'aide d'un oscilloscope, ou sur le signal de sortie à l'aide d'un analyseur de spectre. Le concepteur de PLL veillera donc tout particulièrement au routage sur carte et sur silicium de la PLL.
Ce problème est particulièrement important si on veut intégrer le VCO sur la même puce que le reste de la PLL. En radiofréquence, les PLL avec VCO intégrés n'atteignent jamais les performances spectrales des PLL avec VCO séparé et blindé.
De plus, les capacités du filtre de boucle ne sont pas parfaites et un léger courant de fuite passe à travers chacune de ces capacités. Ce courant génère une chute de tension modulée à la fréquence d'entrée qui se traduit en sortie de la PLL par des fréquences parasites. Ainsi donc le développeur tiendra compte de ce point, par exemple en microélectronique ce courant de fuite est directement proportionnel à l'épaisseur d'oxyde capacitive et à la taille de la capacité.
Parasites extrinsèques[modifier | modifier le code]
Les impuretés extrinsèques sont des fréquences parasites qui viennent de l'extérieur et qui ne sont pas produites par la PLL elle-même. Par exemple des fréquences électromagnétiques externes, des fréquences sur la tension d'alimentation mal filtrée sont traitées par la PLL. C'est pourquoi pour certaines applications nécessitant un spectre de bonne qualité, il est requis un blindage de la structure, notamment du VCO et de la connexion filtre → VCO . À cet effet, on travaillera la compatibilité électromagnétique de la PLL dans le système électronique.
Points de spécification[modifier | modifier le code]
Fréquence d'entrée[modifier | modifier le code]
Fréquence de sortie[modifier | modifier le code]
Frequences maximale et minimale
Bruit de phase[modifier | modifier le code]
exprimé en dBc par hertz, en fonction de la distance à la porteuse.
- en numérique
- Il spécifie la demi-période minimum (sans inclure la gigue) pendant lequel les portes logiques vont pouvoir basculer. Une spécification typique de rapport cyclique pour le numérique est de 55 % / 45 %.
- en analogique mixte
- Le rapport cyclique peut être un facteur direct sur la qualité de sortie, selon l'architecture de démodulation.
Dans ce cas, la spécification sur le rapport cyclique est beaucoup plus restrictive et une méthode classique pour obtenir un bon rapport cyclique est de générer le double de la fréquence escomptée et ensuite de la diviser par une simple bascule : on obtiendra des rapports cycliques de l'ordre de 49 % à 51 %.
- en analogique RF
- Pour des signaux carrés, un rapport cyclique performant est nécessaire, mais il arrive souvent que le système RF nécessite une horloge non pas carrée, mais sinusoïdale. Pour cette dernière, le rapport cyclique n'est plus un critère de spécification.
Notes et références[modifier | modifier le code]
- Michel Fleutry, Dictionnaire encyclopédique d'électronique : anglais-français, Paris, La maison du dictionnaire, , 1054 p. (ISBN 2-85608-043-X) recommande « boucle à phase asservie ».
- (en) M. Khalili Dermani, M. S. Baghaei, F. Colas et M. Rioual, « Non-linear stability analysis of the electrical vehicle chargers power stage connected to the weak grid », CIRED Porto Workshop 2022: E-mobility and power distribution systems, Institution of Engineering and Technology, , p. 955–959 (ISBN 978-1-83953-705-9, DOI 10.1049/icp.2022.0855, lire en ligne, consulté le )
- Cours AU2 Université ISEFC, Syst Asservisseent lineaires P29 -35




























