Analyse structurelle

L'analyse structurelle est une branche de la mécanique des solides qui utilise des modèles simplifiés pour les solides tels que les barres, les poutres et les coques pour la prise de décision technique. Son objectif principal est de déterminer l'effet des charges sur les structures physiques et leurs composants. Contrairement à la théorie de l'élasticité, les modèles utilisés dans l'analyse structurelle sont souvent des équations différentielles à une variable d'espace. Les structures soumises à ce type d'analyse comprennent tout ce qui doit résister à des charges, comme les bâtiments, les ponts, les avions et les navires. L'analyse structurelle utilise des idées de la mécanique appliquée, de la science des matériaux et des mathématiques appliquées pour calculer les déformations, les forces internes, les contraintes (en), les réactions d'appui, la vitesse, les accélérations et la stabilité d'une structure (en) . Les résultats de l'analyse sont utilisés pour vérifier l'aptitude à l'emploi d'une structure, excluant souvent les tests physiques (en) . L'analyse structurelle est donc un élément clé de la conception technique des structures.

Structures et charges

Dans le contexte de l'analyse structurelle, une structure est un corps ou à un ensemble de pièces utilisé pour supporter une charge. Des exemples importants liés au génie civil comprennent les bâtiments, les ponts et les tours ; et dans d'autres branches de l'ingénierie, les charpentes de navires et d'avions, les réservoirs, les appareils sous pression, les systèmes mécaniques et les structures de support électriques sont importants. Pour concevoir une structure, un ingénieur doit tenir compte de sa sécurité, de son esthétique et de sa facilité d'entretien, tout en tenant compte des contraintes économiques et environnementales. D'autres branches de l'ingénierie travaillent sur une grande variété de structures non bâties .

Classement des structures

Un système structurel est la combinaison d’éléments structurels et de leurs matériaux. Il est important pour un ingénieur en structure de pouvoir classer une structure soit par sa forme, soit par sa fonction, en reconnaissant les différents éléments qui composent cette structure. Les éléments structurels guidant les forces systémiques à travers les matériaux ne se comprennent pas seulement comme bielles, treillis, poutre ou colonne, mais aussi câble, arc, cavité ou canal, et même équerre, structure de surface, ou portique.

Charges

Une fois les exigences dimensionnelles d’une structure définies, il devient nécessaire de déterminer les charges que la structure doit supporter. la conception structurelle commence donc par spécifier les charges qui agissent sur la structure. la charge de conception d'une structure est souvent spécifiée dans les codes du bâtiment. Il existe deux types de codes : les codes généraux du bâtiment et les codes de conception. Les ingénieurs doivent satisfaire à toutes les exigences des codes pour que la structure reste fiable.

Il existe deux types de charges auxquelles l’ingénierie des structures doit être confrontée lors de la conception. Le premier type de charges sont les charges mortes constituées du poids des différents éléments structurels et du poids de tous les objets fixés en permanence à la structure. Par exemple, les colonnes, poutres, dalles de plancher, toitures, murs, fenêtres, plomberie, appareils électriques et autres accessoires divers. Le deuxième type de charges sont les surcharges qui varient en ampleur et en emplacement. Il existe de nombreux types de charges vives, telles que les charges de construction, les charges de ponts routiers, les charges de ponts ferroviaires, les charges d'impact, les charges de vent, les charges de neige, les charges sismiques et autres charges naturelles.

Méthodes analytiques

Pour effectuer une analyse précise, un ingénieur en structure doit déterminer des informations telles que les charges structurelles, la géométrie, les conditions de support et les propriétés des matériaux. Les résultats d'une telle analyse incluent généralement les réactions d'appui, les contraintes et les déplacements. Ces informations sont ensuite comparées à des critères indiquant les conditions de défaillance. L'analyse structurelle avancée peut examiner la réponse dynamique, la stabilité et le comportement non linéaire. Il existe trois approches d'analyse : l'approche de la mécanique des matériaux (également connue sous le nom de résistance des matériaux), l'approche de la théorie de l'élasticité (en) (qui est en fait un cas particulier du domaine plus général de la mécanique des milieux continus) et l'approche des éléments finis. Les deux premiers utilisent des formulations analytiques qui appliquent pour la plupart des modèles élastiques linéaires simples, conduisant à des solutions de forme fermée, et peuvent souvent être résolues manuellement. L'approche par éléments finis est en fait une méthode numérique permettant de résoudre des équations différentielles générées par des théories mécaniques telles que la théorie de l'élasticité et de la résistance des matériaux. Cependant, la méthode des éléments finis dépend fortement de la puissance de traitement des ordinateurs et s’applique davantage aux structures de taille et de complexité arbitraires.

Quelle que soit l'approche, la formulation est basée sur les trois mêmes relations fondamentales : équilibre, comportement et compatibilité (en) . Les solutions sont approximatives lorsque l'une de ces relations n'est qu'approximativement satisfaite, ou seulement une approximation de la réalité.

Limites

Chaque méthode présente des limites notables. la méthode de mécanique des matériaux se limite à des éléments structurels très simples dans des conditions de chargement relativement simples. Les éléments structurels et les conditions de chargement autorisés sont cependant suffisants pour résoudre de nombreux problèmes d'ingénierie utiles.

La théorie de l'élasticité permet en principe de résoudre des éléments structurels de géométrie générale dans des conditions de charge générales. la solution analytique se limite toutefois à des cas relativement simples. la solution des problèmes d'élasticité nécessite également la solution d'un système d'équations aux dérivées partielles, ce qui est considérablement plus exigeant mathématiquement que la solution des problèmes de mécanique des matériaux, qui nécessitent tout au plus la solution d'une équation différentielle ordinaire.

La méthode des éléments finis est peut-être à la fois la plus restrictive et la plus utile. Cette méthode elle-même s'appuie sur d'autres théories structurelles (telles que les deux autres discutées ici) pour résoudre les équations. Cependant, elle permet généralement de résoudre ces équations, même avec une géométrie et des conditions de chargement très complexes, avec la restriction qu'il y a toujours une erreur numérique. L’utilisation efficace et fiable de cette méthode nécessite une solide compréhension de ses limites.

Méthodes de résistance des matériaux (méthodes classiques)

La plus simple des trois méthodes discutées ici, la méthode de la mécanique des matériaux, est disponible pour les éléments structurels simples soumis à des chargements spécifiques tels que les barres chargées axialement, les poutres prismatiques en état de flexion pure (en) et les arbres circulaires soumis à la torsion. Les solutions peuvent sous certaines conditions être superposées selon le principe de superposition pour analyser une pièce soumise à un chargement combiné. Des solutions pour des cas particuliers existent pour les structures courantes telles que les récipients sous pression à paroi mince.

Pour l'analyse de systèmes entiers, cette approche peut être utilisée en conjonction avec la statique, donnant naissance à la méthode des sections et à la méthode des nœuds pour l'analyse des treillis, à la méthode de répartition des moments (en) pour les petites charpentes rigides et à la méthode des portiques et cantilever pour les grandes charpentes rigides. À l’exception de la distribution des moments, entrée en vigueur dans les années 1930, ces méthodes ont été développées sous leurs formes actuelles dans la seconde moitié du XIX^e siècle. Ils sont encore utilisés pour les petites structures et pour la conception préliminaire de grandes structures.

Les solutions sont basées sur l’élasticité infinitésimale isotrope linéaire et la théorie des poutres d’Euler–Bernoulli. En d'autres termes, ils contiennent les hypothèses (entre autres) selon lesquelles les matériaux en question sont élastiques, que la contrainte est liée linéairement à la déformation, que le matériau (mais pas la structure) se comporte de manière identique quelle que soit la direction de la charge appliquée, que toutes les déformations, sont petits et que les poutres sont longues par rapport à leur profondeur. Comme pour toute hypothèse simplificatrice en ingénierie, plus le modèle s’éloigne de la réalité, moins le résultat est utile (et plus dangereux).

Exemple

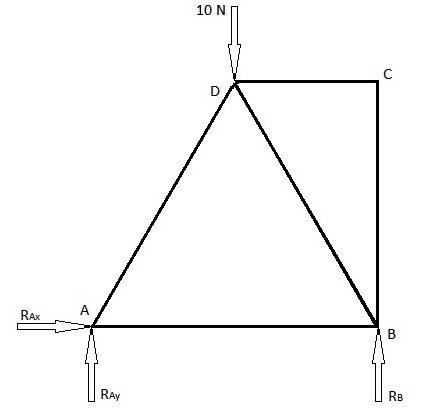
Il existe 2 méthodes couramment utilisées pour trouver les efforts des éléments de treillis, à savoir la méthode des nœuds et la méthode des sections. Vous trouverez ci-dessous un exemple résolu en utilisant ces deux méthodes. Le premier diagramme ci-dessous est le problème présenté pour lequel les forces des éléments de treillis doivent être trouvées. Le deuxième diagramme est le diagramme des chargements et contient les forces de réaction des articulations.

Une treillis triangulaire simple avec des charges imposées.

Puisqu’il y a une articulation en A, elle aura 2 forces de réaction. L’un dans la direction x et l’autre dans la direction y. Au point B, il y a un appui mobile et donc une seule force de réaction dans la direction y. En supposant que ces forces soient dans leurs directions positives respectives (si elles ne sont pas dans les directions positives, la valeur sera négative).

Puisque le système est en équilibre statique, la somme des forces dans n’importe quelle direction est nulle et la somme des moments autour de n’importe quel point est nulle. Ainsi, l’ampleur et la direction des forces de réaction peuvent être calculées.

$\sum M_{A}=0=-10*1+2*R_{B}\Rightarrow R_{B}=5$

$\sum F_{y}=0=R_{Ay}+R_{B}-10\Rightarrow R_{Ay}=5$

$\sum F_{x}=0=R_{Ax}$

Méthode des nœuds

Ce type de méthode utilise l'équilibre des forces dans les directions x et y au niveau de chacun des nœuds de la structure en treillis.

À,

$\sum F_{y}=0=R_{Ay}+F_{AD}\sin(60)=5+F_{AD}{\frac {\sqrt {3}}{2}}\Rightarrow F_{AD}=-{\frac {10}{\sqrt {3}}}$

$\sum F_{x}=0=R_{Ax}+F_{AD}\cos(60)+F_{AB}=0-{\frac {10}{\sqrt {3}}}{\frac {1}{2}}+F_{AB}\Rightarrow F_{AB}={\frac {5}{\sqrt {3}}}$

En D,

$\sum F_{y}=0=-10-F_{AD}\sin(60)-F_{BD}\sin(60)=-10-\left(-{\frac {10}{\sqrt {3}}}\right){\frac {\sqrt {3}}{2}}-F_{BD}{\frac {\sqrt {3}}{2}}\Rightarrow F_{BD}=-{\frac {10}{\sqrt {3}}}$

$\sum F_{x}=0=-F_{AD}\cos(60)+F_{BD}\cos(60)+F_{CD}=-{\frac {10}{\sqrt {3}}}{\frac {1}{2}}+{\frac {10}{\sqrt {3}}}{\frac {1}{2}}+F_{CD}\Rightarrow F_{CD}=0$

En C,

$\sum F_{y}=0=-F_{BC}\Rightarrow F_{BC}=0$

Bien que les forces dans chacun des éléments de treillis soient trouvées, il est recommandé de vérifier les résultats en complétant les bilans de forces restants.

$\sum F_{x}=-F_{CD}=-0=0\Rightarrow verified$

En B,

$\sum F_{y}=R_{B}+F_{BD}\sin(60)+F_{BC}=5+\left(-{\frac {10}{\sqrt {3}}}\right){\frac {\sqrt {3}}{2}}+0=0\Rightarrow verified$

$\sum F_{x}=-F_{AB}-F_{BD}\cos(60)={\frac {5}{\sqrt {3}}}-{\frac {10}{\sqrt {3}}}{\frac {1}{2}}=0\Rightarrow verified$

Méthode des sections

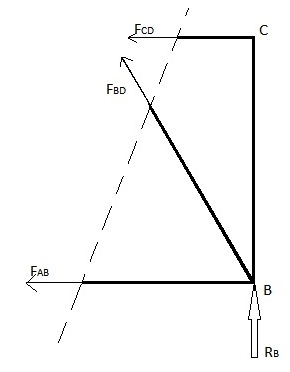
Cette méthode peut être utilisée lorsque les forces des éléments de treillis de quelques éléments seulement doivent être trouvées. Cette méthode est utilisée en introduisant une seule ligne droite traversant l'élément dont la force doit être calculée. Cependant, cette méthode présente une limite dans la mesure où la ligne de coupe ne peut traverser au maximum que 3 éléments de la structure en treillis. Cette restriction est due au fait que cette méthode utilise les équilibres de forces dans les directions x et y ainsi que l'équilibre des moments, ce qui donne un maximum de 3 équations pour trouver un maximum de 3 forces inconnues des éléments de treillis à travers lesquelles cette coupe est réalisée. Trouvez les forces FAB, FBD et FCD dans l'exemple ci-dessus

Méthode 1 : ignorer le côté droit

$\sum M_{D}=0=-5*1+{\sqrt {3}}*F_{AB}\Rightarrow F_{AB}={\frac {5}{\sqrt {3}}}$

$\sum F_{y}=0=R_{Ay}-F_{BD}\sin(60)-10=5-F_{BD}{\frac {\sqrt {3}}{2}}-10\Rightarrow F_{BD}=-{\frac {10}{\sqrt {3}}}$

$\sum F_{x}=0=F_{AB}+F_{BD}\cos(60)+F_{CD}={\frac {5}{\sqrt {3}}}-{\frac {10}{\sqrt {3}}}{\frac {1}{2}}+F_{CD}\Rightarrow F_{CD}=0$

Méthode 2 : ignorer le côté gauche

$\sum M_{B}=0={\sqrt {3}}*F_{CD}\Rightarrow F_{CD}=0$

$\sum F_{y}=0=F_{BD}\sin(60)+R_{B}=F_{BD}{\frac {\sqrt {3}}{2}}+5\Rightarrow F_{BD}=-{\frac {10}{\sqrt {3}}}$

$\sum F_{x}=0=-F_{AB}-F_{BD}\cos(60)-F_{CD}=-F_{AB}-\left(-{\frac {10}{\sqrt {3}}}\right){\frac {1}{2}}-0\Rightarrow F_{AB}={\frac {5}{\sqrt {3}}}$

Les forces des éléments de treillis dans les éléments restants peuvent être déterminées en utilisant la méthode ci-dessus avec une section passant par les éléments restants.

Méthodes d'élasticité

Les méthodes d'élasticité sont généralement disponibles pour un solide élastique de n'importe quelle forme. Des éléments individuels tels que des poutres, des poteaux, des arbres, des plaques et des coques peuvent être modélisés. Les solutions sont dérivées des équations d' élasticité linéaire (en). Les équations d'élasticité sont un système de 15 équations aux dérivées partielles. En raison de la nature des mathématiques impliquées, des solutions analytiques ne peuvent être produites que pour des géométries relativement simples. Pour les géométries complexes, une méthode de résolution numérique telle que la méthode des éléments finis est nécessaire.

Méthodes utilisant l'approximation numérique

Il est courant d'utiliser des solutions approximatives d'équations différentielles comme base pour l'analyse structurelle. Cela se fait généralement à l’aide de techniques d’approximation numérique. L'approximation numérique la plus couramment utilisée en analyse structurelle est la méthode des éléments finis.

La méthode des éléments finis approxime une structure comme un assemblage d'éléments ou de composants avec diverses formes de connexion entre eux et dont chaque élément a une rigidité associée. Ainsi, un système continu tel qu'une plaque ou une coque est modélisé comme un système discret avec un nombre fini d'éléments interconnectés à un nombre fini de nœuds et la rigidité globale est le résultat de l'addition de la rigidité des différents éléments. Le comportement des éléments individuels est caractérisé par la relation de rigidité (ou de flexibilité) de l'élément. L'assemblage des différentes rigidités dans une matrice de rigidité principale qui représente l'ensemble de la structure conduit à la relation de rigidité ou de flexibilité du système. Pour établir la rigidité (ou la flexibilité) d'un élément particulier, on peut utiliser l'approche de la mécanique des matériaux pour les éléments de barres simples unidimensionnels, et l' approche de l'élasticité pour les éléments bidimensionnels et tridimensionnels plus complexes. Le développement analytique et informatique est mieux réalisé au moyen de l'algèbre matricielle, résolvant des équations aux dérivées partielles.

Les premières applications des méthodes matricielles ont été appliquées aux cadres articulés avec des éléments de treillis, de poutres et de colonnes ; les méthodes matricielles ultérieures et plus avancées, appelées « analyse par éléments finis (en) », modélisent une structure entière avec des éléments à une, deux et trois dimensions et peuvent être utilisées pour des systèmes articulés ainsi que des systèmes continus tels qu'un récipient sous pression, des plaques, coques et solides tridimensionnels. Les logiciels informatiques commerciaux pour l'analyse structurelle utilisent généralement l'analyse matricielle par éléments finis, qui peut être classée en deux approches principales : la méthode de rigidité (en) et la méthode de flexibilité (en). la méthode de rigidité est de loin la plus populaire grâce à sa facilité de mise en œuvre ainsi que de formulation pour des applications avancées. la technologie des éléments finis est désormais suffisamment sophistiquée pour gérer à peu près n’importe quel système, à condition qu’une puissance de calcul suffisante soit disponible. Son applicabilité inclut, sans s'y limiter, l'analyse linéaire et non linéaire, les interactions solides et fluides, les matériaux isotropes, orthotropes ou anisotropes, ainsi que les effets externes qui sont des facteurs statiques, dynamiques et environnementaux. Cela n’implique cependant pas que la solution calculée sera automatiquement fiable car beaucoup dépend du modèle et de la fiabilité des données saisies.

Chronologie

• 1452-1519 Léonard de Vinci a apporté de nombreuses contributions
• 1638 : Galileo Galilei publie le livre " Discours concernant deux sciences nouvelles " dans lequel il examine la défaillance de structures simples.
• 1660 : loi de Hooke par Robert Hooke
• 1687 : Isaac Newton publie « Philosophiæ naturalis principia mathematica » qui contient les lois du mouvement de Newton.
• 1750 : équation de poutre d'Euler – Bernoulli
• 1700-1782 : Daniel Bernoulli introduit le principe du Principe des puissances virtuelles
• 1707-1783 : Leonhard Euler développe la théorie du Flambage des colonnes
• 1826 : Henri Navier publie un traité sur les comportements élastiques des structures
• 1873 : Carlo Alberto Castigliano présente sa thèse « Intorno ai sistemi elastici », qui contient son théorème pour calculer le déplacement comme dérivée partielle de l'énergie de déformation. Ce théorème inclut la méthode du « moindre travail » comme cas particulier
• 1878-1972 Stephen Timoshenko père de la mécanique appliquée moderne, y compris la théorie des poutres Timoshenko-Ehrenfest (en)
• 1936 : publication par Hardy Cross (de) de la méthode de répartition des moments qui fut plus tard reconnue comme une forme de méthode de relaxation applicable au problème de l'écoulement dans les réseaux de canalisations.
• 1941 : Alexander Hrennikoff (en) soumet son D.Sc. thèse au MIT sur la discrétisation de problèmes d'élasticité plane à l'aide d'un cadre en treillis
• 1942 : R. Courant divise un domaine en sous-régions finies
• 1956 : L'article de J. Turner, RW Clough, HC Martin et LJ Topp Stiffness and Deflection of Complex Structures introduit l'expression « finite-element method » et est largement reconnu comme le premier traitement complet de la méthode telle qu'elle est connue aujourd'hui

Voir aussi

• Statique structurelle
• Geometrically and materially nonlinear analysis with imperfections included (en) - Analyse géométriquement et matériellement non linéaire avec imperfections incluses
• Conception aux états limites
• Théorie de l'ingénierie structurelle
• Intégrité structurelle et défaillance
• Analyse contrainte-déformation
• critère de rendement de von Mises
• Évaluation probabiliste des structures
• Tests structurels

Voir aussi

Notices d'autorité :

• LCCN
• GND
• Israël
• Tchéquie