Effet Néel
L’effet Néel apparaît lorsqu’un matériau superparamagnétique placé à l’intérieur d’une bobine conductrice est soumis à des champs magnétiques de fréquences différentes. La non-linéarité du matériau superparamagnétique agit comme un mélangeur de fréquences. La tension mesurée aux bornes de la bobine comprend alors plusieurs composantes fréquentielles, non seulement aux fréquences d’origine, mais aussi à certaines de leurs combinaisons linéaires. Ainsi, la transposition en fréquence du champ à mesurer permet de détecter un champ produit par un courant continu avec une simple bobine.
« Effet Néel » et « Neel Effect » sont des marques déposées et détenues par la société Neelogy[1].
Histoire
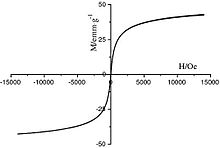
Le physicien français Louis Néel (1904-2000) a découvert en 1949 que des matériaux ferromagnétiques finement divisés en nanoparticule perdent toute hystérésis en deçà d’une certaine taille critique[2],[3]. On appelle ce phénomène le superparamagnétisme. L’aimantation de ces matériaux en fonction du champ qui leur est appliqué est fortement non linéaire comme on le voit sur sa représentation graphique en figure 1. Cette courbe est bien décrite par la fonction de Langevin mais pour de faibles champs on peut l’écrire plus simplement sous forme de développement limité :
où est la susceptibilité à champ nul et est appelé coefficient de Néel. Le coefficient de Néel rend compte de la non-linéarité des matériaux superparamagnétiques à faible champ.
Principe

L’effet Néel apparaît lorsque :
- on place un matériau superparamagnétique à l’intérieur d’une bobine parcourue par un courant d’excitation alternatif de fréquence et
- on soumet ladite bobine à un champ magnétique extérieur , statique ou périodique de fréquence .
Alors, quand on mesure la tension u(t) aux bornes de la bobine en présence du matériau superparamagnétique, on observe l’apparition de nouvelles composantes fréquentielles en plus de la (ou des) fréquence(s) d’origine. Ces composantes d’intermodulation apparaissent à des combinaisons linéaires déterminées de et . Par exemple, si le champ magnétique extérieur est statique alors il apparaît une composante de tension à 2. Si le champ extérieur est périodique alors il apparaît une composante de tension à 2 + . On observe également des composantes à des ordres supérieurs mais d’intensité moins grande. On montre par le calcul que c’est le comportement non linéaire du matériau superparamagnétique qui entraîne l’intermodulation des fréquences du champ magnétique. Le matériau agit comme un mélangeur.
La physique de l'effet Néel

Soit une bobine de N spires de surface S parcourue par un courant d’excitation et plongée dans un champ magnétique colinéaire à l’axe de la bobine. Un matériau superparamagnétique est déposé à l’intérieur de la bobine. La force électromotrice (f.é.m.) aux bornes d’une spire de la bobine, e, est donnée par la formule bien connue :
où B est l’induction magnétique, elle-même donnée par l’équation :
- En l’absence de matériau magnétique
et
En dérivant cette expression de , il vient de toute évidence que les fréquences de la tension sont les mêmes que celles du courant d’excitation et/ou le champ magnétique .
- En présence de matériau superparamagnétique
En négligeant les termes supérieurs du développement limité, on obtient pour B :
De nouveau la dérivation du premier terme de l’équation fournit des composantes de tension aux fréquences du courant d’excitation et/ou du champ magnétique .
En revanche le développement du deuxième terme multiplie des composantes de fréquence différentes ce qui intermodule les fréquences de départ et génère des composantes à leurs combinaisons linéaires.
La non-linéarité du matériau superparamagnétique agit comme un mélangeur de fréquences.

En appelant le champ magnétique total à l’intérieur de la spire située à l’abscisse , en intégrant l’induction ci-dessus le long de la bobine entre les abscisses et , et en dérivant par rapport à , il vient :
On retrouve les termes classiques d’auto-inductance et d’effet Rogowski tous deux aux fréquences d’origine. Le troisième terme est dû à l’effet Néel. Il rend compte de l’intermodulation entre le courant d’excitation et le champ externe. Lorsque le courant d’excitation est sinusoïdal, l’effet Néel se caractérise par l’apparition d’une harmonique 2, porteuse de l’information de circulation de champ :
avec
Applications
Le capteur de courant à effet Néel

Une application importante de l’effet Néel est la mesure du champ magnétique rayonné par un conducteur lorsqu’il est parcouru par un courant[4]. C’est le principe des capteurs de courant à effet Néel[5], qui ont été développés et brevetés par la société Neelogy. L’intérêt de l’effet Néel est en particulier de permettre la mesure précise de courants continus ou de très faible fréquence avec un capteur du type transformateur de courant, sans contact.
Le transducteur d’un capteur de courant à effet Néel est constitué d’une bobine dont le noyau est un composite chargé de nanoparticules superparamagnétiques. La bobine est parcourue par un courant d’excitation . En présence d’un champ magnétique extérieur à mesurer , le transducteur transpose par effet Néel l’information à mesurer, H(f), autour d’une fréquence porteuse, l’harmonique de rang 2 du courant d’excitation 2, à laquelle la mesure est facilitée. Autrement dit la force électromotrice générée par la bobine est proportionnelle au champ magnétique à mesurer, et au carré du courant d’excitation :
Pour améliorer les performances de la mesure (linéarité, sensibilité à la température, sensibilité aux vibrations, etc.), le capteur comprend aussi un second bobinage de contre-réaction permettant d’annuler en permanence la seconde harmonique. La relation entre le courant de contre-réaction et le courant primaire est alors purement proportionnelle au nombre de spires de contre réaction ().
Autres applications de l’effet Néel
L’effet Néel « mélange » les fréquences de différents champs magnétiques en présence d’un matériau superparamagnétique. Dans le capteur de courant à effet Néel présenté ci-dessus, on utilise un transducteur mettant en œuvre ensemble une quantité fixe de matériau superparamagnétique et un champ connu généré par le courant de la bobine d’excitation pour déterminer un champ extérieur d’amplitude inconnue. Mais on peut aussi utiliser un transducteur mettant en œuvre ensemble deux champs magnétiques connus de fréquences différentes pour déterminer une quantité inconnue d’un matériau superparamagnétique. On connait deux applications de ce type dans des « détecteurs » de nanoparticules superparamagnétiques. À partir d’un brevet russe[6], Magnisense[7],[8] développe des immunoessais magnétiques (en) qui utilisent des nanoparticules magnétiques comme marqueurs d’organismes ou de molécules biologiques détectés de façon très sensible et précise par le lecteur MIAtek[9]. Par ailleurs Philips développe une technique d’imagerie de particules[10] (imagerie à particules magnétiques (en)) pour des applications de diagnostic médical in vivo.
Notes et références
- Bases de données Marques, Institut national de la propriété industrielle.
- Louis Néel, Comptes rendus hebdomadaires des séances de l'Académie des sciences, 1949/01 (T228)-1949/06, p. 664-666.
- Louis Néel, « Théorie du traînage magnétique des ferromagnétiques en grains fins avec applications aux terres cuites », dans Annales de géophysique, t. V, fasc. 2, février 1949, p. 99-136.
- Capteurs de champ magnétique et de courant, procédé de commande et noyau magnetique pour ces capteurs, « Brevet FR 2891917 ».
- Procédé de mesure de courant au moyen d'un capteur de circulation de champs magnétiques de forme spécifique, et système obtenu à partir d'un tel procédé, « Brevet FR 2971852 »
- (en) P.I.Nikitin, P.M. Vetoshko, T.I Ksenevich, « Magnetic Immunoassays », Sensor Letters, vol. 5, 1-4, 2007.
- (en) « Magnetic immunoassays: A new paradigm in POCT » « Copie archivée » (version du sur Internet Archive), article ivd technology, 1er juillet 2008.
- (en) « Magnisense», site officiel.
- (en) « MIAtek Technology».
- (en) Bernhard Gleich, Jürgen Weizenecker, « Tomographic imaging using the nonlinear response of magnetic particles », Nature, vol. 435, p. 1214–1217, 30 juin 2005.






















![{\displaystyle u(t)=L{\frac {dI(t)}{dt}}+F_{Rog}{\frac {d}{dt}}\left[\int _{0}^{Lp}H(l)dl\right]+F_{Neel}\left[\int _{0}^{Lp}H(l)dl\right]I(t){\frac {dI(t)}{dt}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb0e7bc6abbbaa174f7b5af1ae9536c58986fea4)
![{\displaystyle u(t)=LI_{ex}w_{ex}\cos {w_{ex}t}+F_{Rog}{\frac {d}{dt}}\left[\int _{0}^{Lp}H(l)dl\right]+F_{Neel}\left[\int _{0}^{Lp}H(l)dl\right]{\frac {I_{ex}^{2}}{2}}w_{ex}\sin {2w_{ex}t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7037673352db1e6e877c4d709c335e32f10490da)




