YUV

Exemple d'une plage U-V, où Y = 0,5, représenté à l'intérieur de la gamme de couleurs RVB ; en noir et blanc, seule Y est utilisée, toutes ces couleurs rendent donc le même gris

Décomposition d'une image en YUV

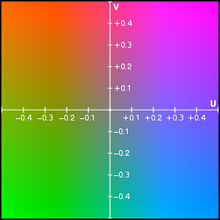
Le modèle YUV définit un espace colorimétrique en trois composantes. La première, Y, représente la luminance et les deux autres, U et V, représentent la chrominance. YUV est utilisé dans le système de diffusion télévisuelle PAL. Le NTSC utilise l'espace YIQ. Le système SÉCAM utilise quant à lui l'espace colorimétrique YDbDr, dérivé de YUV.

Dans le traitement des signaux vidéo couleur, on ajuste les coefficients des signaux U et V de telle sorte que la valeur crête à crête soit égale à la valeur maximale de Y, soit 0,7 V.

Équations

Le signal YUV est créé depuis une source RGB (rouge, vert et bleu). Les valeurs de R, G et B sont additionnées selon leur poids relatif pour obtenir le signal Y. Ce dernier représente la luminance de la source. Le signal U est obtenu en soustrayant le Y du signal bleu d'origine ; de façon similaire le V est obtenu en soustrayant Y du signal rouge. Ces opérations peuvent facilement être réalisées au moyen d'un circuit analogique.

Les équations suivantes peuvent être utilisées pour dériver Y, U et V à partir des composantes R, G et B :

(R, G, B, Y) ∈ [0 ; 1]⁴

U ∈ [−0,436 ; 0,436]

V ∈ [−0,615 ; 0,615]

Cependant, les limites autorisées sur U et V dépendent de Y.

De RVB à YUV :

Y = 0,299⋅R + 0,587⋅G + 0,114⋅B

U = 0,492⋅(B − Y) = −0,14713⋅R − 0,28886⋅G + 0,436⋅B

V = 0,877⋅(R − Y) = 0,615⋅R − 0,51498⋅G- 0,10001⋅B

De YUV à RVB :

R = Y + 1,13983⋅V

G = Y − 0,39465⋅U − 0,58060⋅V

B = Y + 2,03211⋅U

Ou en utilisant ces matrices :

$\begin{bmatrix} Y \\ U \\ V \end{bmatrix} = \begin{bmatrix} 0,299 & 0,587 & 0,114 \\ -0,14713 & -0,28886 & 0,436 \\ 0,615 & -0,51498 & -0,10001 \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix}$

$\begin{bmatrix} R \\ G \\ B \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1,13983 \\ 1 & -0,39465 & -0,58060 \\ 1 & 2,03211 & 0 \end{bmatrix} \begin{bmatrix} Y \\ U \\ V \end{bmatrix}$

Ces coefficients sont empiriques.

Voir aussi

• Système colorimétrique