Wikipédia:Lumière sur/Théorème de Robertson-Seymour
Ce « Lumière sur » a été ou sera publié sur la page d'accueil de l'encyclopédie le mercredi 4 janvier 2012.
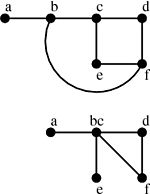
En mathématiques, et plus précisément en théorie des graphes, le théorème de Robertson-Seymour (parfois également appelé le théorème des mineurs, et connu, avant qu'il soit démontré, sous le nom de conjecture de Wagner), est un théorème démontré en 2004 par Neil Robertson et Paul Seymour. Considéré généralement comme un des résultats les plus importants de la théorie des graphes, il se caractérise par une démonstration extrêmement complexe et délicate, dont la publication, comportant plus de cinq cents pages, s'étala de 1983 à 2004 dans vingt articles de la revue Journal of Combinatorial Theory.
Le théorème de Robertson–Seymour affirme que « sur l'ensemble des graphes non orientés, l'ordre partiel défini par la relation « être un mineur » est un bel ordre ». Ce résultat est équivalent à dire que toute famille F de graphes fermée, c'est-à-dire telle que les mineurs des graphes de F appartiennent aussi à F, peut être caractérisée par un ensemble fini de « mineurs exclus », de la même manière que le théorème de Kuratowski caractérise les graphes planaires comme ceux dont aucun mineur n'est le graphe complet K5, ni le graphe K3,3 de l'énigme des trois maisons.
Bien que le théorème lui-même ne soit pas constructif (on ne connaît d'ailleurs explicitement de listes de mineurs exclus que dans très peu de cas), Robertson et Seymour ont montré qu'il avait d'importantes conséquences en théorie de la complexité, garantissant l'existence d'algorithmes rapides pour de nombreux problèmes de décision.
