Pendule de Newton

Le pendule de Newton est un pendule se composant de cinq billes et permettant d'illustrer les théories de conservation de la quantité de mouvement et de l'énergie.

Description

Le pendule de Newton se compose de cinq billes métalliques indéformables de même masse suspendues par deux fils à deux barres rigides. Ces cinq billes se touchent au repos et sont situées dans le plan médian des deux barres. Son fonctionnement est fondé sur le principe d'inertie d'un système (pendule + Terre) que l'on supposera isolé (pas de frottement) et de la conservation de l'énergie mécanique pour un tel système.

Expériences

Avant l'impact Après l'impact
Variantes de mouvements du pendule de Newton.

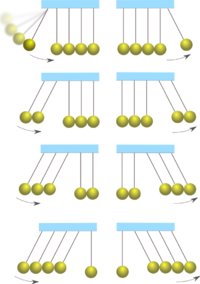
Lorsqu'on lance deux billes, de l'autre côté deux billes se mettent en mouvement. Lorsqu'on lance trois billes, de l'autre côté les deux billes restantes se mettent en mouvement, accompagnées de la bille les ayant percutées. Il en est de même pour quatre billes.

Expériences plus méconnues : si l'on lance une bille de chaque côté en même temps, celles-ci rebondissent en même temps alors que les trois du milieu restent immobiles. De même, avec deux billes de chaque côté, la dernière bille est immobile. Si l'on lance trois billes d'un côté et deux de l'autre, elles se percutent et vont trois dans un sens, deux dans l'autre, alternativement.

Enlever une bille au repos alors qu'une autre effectue un mouvement de l'autre côté décale le mouvement d'une bille.

Il est possible de lancer plusieurs billes à des instants différents, afin d'augmenter le nombre de mouvements et de chocs, mais les résultats sont souvent faussés par les influences extérieures et par la non-perfection du matériel.

Interprétation conservative

Le principe du pendule repose à la fois sur deux principes de conservation qui concernent respectivement l'énergie mécanique et la quantité de mouvement.

Cas où on lance une bille

L'interprétation est ici plus aisée en considérant un pendule avec uniquement deux billes. Dans cette analyse, les principes de conservation évoqués conduisent à un système de deux équations où les caractéristiques du pendule, avant et après la collision des billes, sont reliées. Avec les données de départ sur les billes que sont la vitesse initiale nulle de l'une d'entre elles et l'égalité de leur masse, la résolution du système permet de trouver la vitesse respective des deux billes après leur collision. On constate alors que l'effet du choc a simplement consisté en l'échange de la vitesse et donc de l'énergie entre les deux billes.

Démonstration :

Il est trivial d'avancer qu'à la suite d'un choc de billes sur un côté du pendule, ce sont les billes de l'autre côté qui seront éjectées. Cela à cause de la conservation de la quantité de mouvement, qui est vectorielle et initialement orientée dans un sens. Considérons le système comme quasi-isolé de sorte que la quantité de mouvement est conservée, et limitons nous dans un premier temps, à un pendule à deux billes. Appliquons cette loi de conservation juste avant et après le choc. La bille lâchée à une certaine hauteur rencontre l'autre à la vitesse $v$ . Après le choc, faisons l'hypothèse que les deux billes sont animées des vitesses inconnues $v'$ pour celle qui est tombée et $v''$ pour celle qui a subi le choc. Nous pouvons écrire la relation générale :

${\begin{aligned}{\overrightarrow {P_{i}}}={\overrightarrow {P_{f}}}&\Rightarrow m{\overrightarrow {v}}=m{\overrightarrow {v}}'+m{\overrightarrow {v}}''\\&\Rightarrow v=v'+v''\,(1)\end{aligned}}$

La seule force en présence étant la pesanteur, qui est une force conservative, l'énergie mécanique est conservée. L'énergie potentielle des deux billes ( $2\times mgh$ ) est la même avant et après le moment du choc. Au moment du choc, les deux billes sont à la même hauteur $h$ . Ainsi :

${\begin{aligned}E_{i}=E_{f}&\Rightarrow {\frac {1}{2}}mv^{2}+2mgh={\frac {1}{2}}mv'^{2}+{\frac {1}{2}}mv''^{2}+2mgh\\&\Rightarrow v^{2}=v'^{2}+v''^{2}\,\left(2\right)\end{aligned}}$

On a donc

$v^{2}-v'^{2}=v''^{2}=(v-v')(v+v').$

Mais par (1), $v-v'=v'',$ donc

$v''=v+v'.$

Injectons cette relation dans (1), pour obtenir

$v'=0,\quad v''=v.$

De ceci, il découle qu'après le choc, la première bille est au repos tandis que la seconde bille est animée de la vitesse de la première bille avant le choc.

Revenons maintenant à notre pendule à $n$ billes. À partir du cas d'un pendule à deux billes, nous pouvons aisément considérer qu'en intercalant n'importe quoi de rigide et indéformable, entre les deux billes, nous observerons un comportement similaire. La bille initialement lâchée, percutera l'objet et s'immobilisera, transférant son énergie et sa quantité de mouvement à la bille au contact de la face opposée de l'objet par l'intermédiaire de ce dernier. Physiquement, le choc de la première bille génère une onde acoustique dans l'objet qui propage l'énergie de la bille en direction de l'autre bille. Dans le cas où l'objet intermédiaire est une bille ou plusieurs billes identiques aux deux premières, l'énergie transportée par l'onde sera totalement transmise à la dernière bille qui n'aura de choix que de s'élever du côté opposé aux choc. Pour démontrer ceci, il suffit d'appliquer le même raisonnement que celui qui est utilisé ci-dessous dans le cas d'un lancer initial de deux billes. Pour éviter une redondance fastidieuse nous laisserons au lecteur curieux ou sceptique le soin de s'adonner à cet exercice. Nous noterons enfin, qu'il est remarquable que les phénomènes mis en œuvre dans le pendule de Newton font intervenir à la fois la mécanique du solide et la mécanique ondulatoire soit une grande partie des connaissances en physique de la fin du XIX^e siècle.

En conclusion, si on lance une bille d'un côté d'un pendule de Newton sur plusieurs autres immobiles, cette bille s'arrête après le choc tandis que celle située à l'autre extrémité se soulève en récupérant le mouvement de la bille initialement lancée.

Cas où on lance deux billes

Les deux billes de l'extrémité opposée se soulèvent car elles sont percutées par deux impacts éloignés temporairement de peu de temps^[pas clair].

Autre approche :

Restons dans le cas où les deux billes lancées percutent simultanément les autres billes initialement au repos. Faisons l'hypothèse qu'un nombre inconnu $n$ de billes partent après le choc à la même vitesse $v'$ et appliquons la conservation de la quantité de mouvement au moment du choc.

Nous allons déterminer le nombre inconnu $n$ de billes qui s'élèvent après le choc et par la suite vérifier, dans ce cas, l'hypothèse de vitesses identiques pour ces dernières.

La vitesse des deux billes qui tombent, au moment du choc, est $v$ et toutes les billes ont la même masse $m$ . À cet instant, les vecteurs vitesses sont horizontaux et orientés dans la même direction, donc :

${\begin{aligned}{\overrightarrow {P_{i}}}={\overrightarrow {P_{f}}}&\Rightarrow 2m{\overrightarrow {v}}=n\times m{\overrightarrow {v}}'\Rightarrow 2v=nv'\\&\Leftrightarrow v={\frac {1}{2}}nv'\,(3)\end{aligned}}$

La conservation de l'énergie mécanique donne :

${\begin{aligned}E_{i}=E_{f}&\Rightarrow {\frac {1}{2}}2mv^{2}+5mgh={\frac {1}{2}}n\times mv'^{2}+5mgh\\&\Rightarrow 2v^{2}=nv'^{2}\,(4)\end{aligned}}$

Éliminons, dans cette deuxième relation $\left(4\right)$ , la vitesse $v$ en se servant de la première $\left(3\right)$ , puis simplifions l'expression :

${\begin{aligned}(3)\,\&\,(4)&\Rightarrow 2\times {\frac {1}{4}}n^{2}v'^{2}=nv'^{2}\\&\Rightarrow {\boldsymbol {n=2}}\end{aligned}}$

Nous venons de démontrer que lorsque deux billes sont lancées, deux billes s'élèveront après le choc des deux premières sur les trois autres. Vérifions maintenant notre hypothèse de départ concernant les vitesses dans l'état final pour le cas où $n=2$ . Appelons ${\overrightarrow {v}}_{1}$ et ${\overrightarrow {v}}_{2}$ les vecteurs vitesse des billes qui s'élèvent à la suite du choc. Appliquons à nouveau la conservation de l'énergie et de l'impulsion :

${\begin{aligned}E_{i}=E_{f}&\Rightarrow {\frac {1}{2}}2mv^{2}+5mgh={\frac {1}{2}}mv_{1}^{2}+{\frac {1}{2}}mv_{2}^{2}+5mgh\\&\Rightarrow 2v^{2}=v_{1}^{2}+v_{2}^{2}\,\left(5\right)\end{aligned}}$

${\begin{aligned}{\overrightarrow {P_{i}}}={\overrightarrow {P_{f}}}&\Rightarrow 2m{\overrightarrow {v}}=m{\overrightarrow {v}}_{1}+m{\overrightarrow {v}}_{2}\\&\Rightarrow 2v=v_{1}+v_{2}\\&\Leftrightarrow v={\frac {1}{2}}\left(v_{1}+v_{2}\right)\,\left(6\right)\end{aligned}}$

En remplaçant cette expression $\left(6\right)$ de la vitesse dans la formule précédente $\left(5\right)$ , il vient :

${\begin{aligned}2\times {\frac {1}{4}}\left(v_{1}+v_{2}\right)^{2}=v_{1}^{2}+v_{2}^{2}&\Leftrightarrow v_{1}^{2}+v_{2}^{2}+2v_{1}v_{2}=2v_{1}^{2}+2v_{2}^{2}\\&\Leftrightarrow v_{1}^{2}+v_{2}^{2}-2v_{1}v_{2}=0\\&\Leftrightarrow \left(v_{1}-v_{2}\right)^{2}=0\\&\Leftrightarrow {\boldsymbol {v_{1}=v_{2}}}\end{aligned}}$

Nous en concluons que les billes du pendule de Newton connaissent les lois de conservation de la physique. Quand deux billes sont lancées, deux billes s'élèveront à la suite du choc avec la même vitesse. Quelle est cette vitesse ? Partant de ce que nous venons d'établir ( $n=2$ et $v_{1}=v_{2}=v'$ ) et utilisant de nouveau la conservation de la quantité de mouvement nous pouvons écrire :

${\begin{aligned}{\overrightarrow {P_{i}}}={\overrightarrow {P_{f}}}&\Rightarrow 2m{\overrightarrow {v}}=m{\overrightarrow {v}}'+m{\overrightarrow {v}}'=2m{\overrightarrow {v}}'\\&\Rightarrow 2v=2v'\\&\Leftrightarrow {\boldsymbol {v'=v}}\end{aligned}}$

Le même résultat serait obtenu par l'application de la conservation de l'énergie. Les deux billes qui s'élancent dans l'état final ont toutes les deux la même vitesse, égale à celle des billes lancées au moment du choc.

Cas où on lance trois billes ou plus

Pour le traitement mathématique de la collision d’une « chaîne » consistant en plus de 2 billes, les lois de conservation de la quantité de mouvement et de l’énergie cinétique ne sont plus suffisantes. Admettons qu’il y ait 5 billes ; les conditions initiales connues, on a besoin de 5 équations pour déterminer les 5 vitesses finales.

Effectivement, pour expliquer le comportement de la chaîne avec plus de 2 billes, il faut tenir compte d’une propriété particulière du dispositif : on considère la « chaîne » comme un système composé de masses et de ressorts (comme on le fait pour traiter les oscillations d’un réseau cristallin). Dans ce système se propage une onde. Ce n’est que si cette propagation se déroule sans dispersion, qu’il résulte le comportement observé avec les billes. Si les ressorts respectent la loi de Hooke, on a une forte dispersion, et l’expérience ne se déroule pas comme on l’observe avec les billes. Ceci se montre facilement sur un rail à coussin d’air. Un système de — par exemple — 5 chariots plus des ressorts comme butoirs ne se comporte pas comme les billes. Quand on lance deux chariots contre les trois autres qui se trouvent au repos, il résulte un mouvement assez chaotique. La non-dispersion de la chaîne de billes vient du fait que les ressorts équivalents qui correspondent à la pression d'une sphère sur une autre, n'est pas du tout du type loi de Hooke.

Autre approche du problème :

Généralisons le raisonnement utilisé pour le cas d'un lancer de 2 billes à un lancer d'un nombre $n$ indéterminé de billes. Dans l'hypothèse où les billes, à la suite du choc, ont la même vitesse $v'$ quel est ne nombre $n'$ de billes qui s'élèveront dans après le choc ? Enfin, dans un souci de généralisation, notons que le nombre total de billes ( $n''=n+n'$ ) que possède notre pendule est lui aussi indéterminé. Appliquons de nouveau les lois de conservation :

${\begin{aligned}E_{i}=E_{f}&\Rightarrow {\frac {1}{2}}n\times mv^{2}+n''mgh={\frac {1}{2}}n'\times mv'^{2}+n''mgh\\&\Rightarrow nv^{2}=n'v'^{2}\,\left(7\right)\end{aligned}}$

${\begin{aligned}{\overrightarrow {P_{i}}}={\overrightarrow {P_{f}}}&\Rightarrow n\times m{\overrightarrow {v}}=n'\times m{\overrightarrow {v}}'\\&\Rightarrow nv=n'v'\\&\Leftrightarrow v={\frac {n'}{n}}v'\,\left(8\right)\end{aligned}}$

En remplaçant cette seconde expression $\left(8\right)$ dans la première $\left(7\right)$ , il vient :

$n\left({\frac {n'}{n}}\right)^{2}v'^{2}=n'v'^{2}\Rightarrow {\boldsymbol {n=n'}}$

Comme dans le cas d'un lancer de 2 billes, vérifions notre hypothèse concernant la vitesse des billes après le choc. Nous avons montré que les vitesses des billes étaient égales dans l'état final dans le cas où une ou deux billes étaient lancées dans l'état initial. Faisons l'hypothèse que ceci est vérifié à l'ordre ( $n-1$ ). Qu'en est-il à l'ordre $n$ ? pour répondre à la question, on part de l'expression des lois de conservation à l'ordre ( $n-1$ ) et on ajoute la contribution d'une bille supplémentaire dans l'état initial sans préjuger du comportement en vitesse $v'$ de la bille supplémentaire dans l'état final (termes en gras dans les formules ci-dessous). Bien entendu, la bille supplémentaire, dans l'état initial, à la même vitesse $v$ que les autres qui l'accompagnent. Dans un souci de généralisation nous ne présumons toujours pas du nombre de billes ( $n''$ ) qui composent le pendule. Nous écrivons ainsi :

${\begin{aligned}E_{i}=E_{f}&\Rightarrow {\frac {1}{2}}(n-1)mv^{2}{\boldsymbol {+{\frac {1}{2}}mv^{2}}}+n''mgh={\frac {1}{2}}(n-1)mv^{2}{\boldsymbol {+{\frac {1}{2}}mv'^{2}}}+n''mgh\\&\Rightarrow nv^{2}=(n-1)v^{2}+v'^{2}\,\left(9\right)\end{aligned}}$

${\begin{aligned}{\overrightarrow {P_{i}}}={\overrightarrow {P_{f}}}&\Rightarrow (n-1)m{\overrightarrow {v}}{\boldsymbol {+m{\overrightarrow {v}}}}=(n-1)m{\overrightarrow {v}}+{\boldsymbol {m{\overrightarrow {v}}'}}\\&\Rightarrow nv=(n-1)v+v'\\&\Leftrightarrow v={\frac {n-1}{n}}v+{\frac {1}{n}}v'\,\left(10\right)\end{aligned}}$

On substitue cette dernière expression $\left(10\right)$ dans la première $\left(9\right)$ pour obtenir la relation suivante :

${\begin{aligned}n\left({\frac {n-1}{n}}v+{\frac {1}{n}}v'\right)^{2}=(n-1)v^{2}+v'^{2}\Leftrightarrow \quad &(n-1)^{2}v^{2}+v'^{2}+2(n-1)vv'=n(n-1)v^{2}+nv'^{2}\\\Leftrightarrow \quad &(n-1)(v-v')^{2}=0\\\Rightarrow \quad &{\boldsymbol {v'=v}}\\\end{aligned}}$

Puisque nous sommes dans le cas où $n\geq 3$ , les vitesses des billes dans l'état final doivent être les mêmes et égales à la vitesse des billes dans l'état initial.

En conclusion, pour un pendule de Newton d'un nombre quelconque de billes supérieur à 1, si $n$ billes sont lâchées simultanément et percutent les autres à la vitesse $v$ , après le choc, le même nombre $n$ de billes s’élèveront, du lieu du choc et du côté opposé au choc, à la même vitesse et donc, avec la même énergie.

Histoire et éponymie

John Wallis, Christopher Wren et Christiaan Huygens présentèrent tous trois à la Royal Society en 1662 des mémoires décrivant les principes à l'œuvre dans ce pendule. Newton n'y a donc eu aucune part. René Descartes avait avant eux eu l'idée de la conservation du moment cinétique, mais sa solution du problème n'était pas complète.