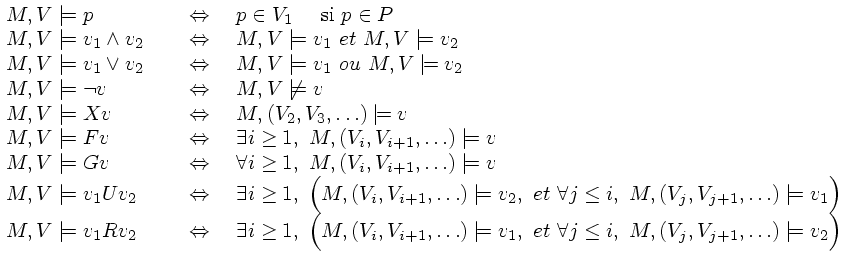Logique temporelle
La logique temporelle est une branche de la logique mathématique et plus précisément de la logique modale, qui est formalisée de plusieurs manières. La caractéristique commune de ces formalisations réside en l'ajout de modalités (autrement dit de « transformateurs de prédicats ») liées au temps ; par exemple, une formule typique de la logique modale est la formule , qui se lit : « la formule est satisfaite jusqu'à ce que la formule le soit » et qui signifie que l'on cherche à garantir qu'une certaine propriété (ici ) est satisfaite pendant tout le temps qui court avant qu'une autre formule (ici ) le soit.
D'un point de vue sémantique, cela signifie que la notion de vérité dans ces logiques prend en compte l'évolution du monde. C'est-à-dire qu'une proposition peut être, à un moment, satisfaite, puis plus tard, ne plus l'être.
Plusieurs formalisations de la logique temporelle ont été décrites, prenant en compte diverses modalités de base.
La logique temporelle est très utilisée en vérification formelle, où la technique de base est essentiellement le model checking. On peut, par exemple, y exprimer le fait qu'un événement dangereux ne doit pas survenir tant qu'une certaine condition de sécurité n'est pas satisfaite.
Définition[modifier | modifier le code]
Dans cet article, seul est présenté le calcul des propositions temporel, autrement dit un calcul des propositions augmenté de modalités temporelles, qui sera néanmoins appelé « logique temporelle ».
Ces logiques sont définies sur un ensemble de propositions atomiques P ou variables de propositions. Ces propositions atomiques sont combinées par un certain nombre de connecteurs logiques, dont les connecteurs usuels : et, ou, non, implication, ainsi que d'autres opérateurs que l'on appelle des modalités. La logique temporelle est donc une logique modale. Dans le cas de la logique temporelle linéaire (LTL), on ajoute les modalités suivantes
- X : demain ou immédiatement après (à distinguer donc du don't care en logique classique noté aussi X) (la lettre X vient de l'anglais next : « suivant »)
- F : un jour (la lettre F vient de l'anglais finally : « finalement »)
- G : toujours (la lettre G vient de l'anglais globally : « globalement »)
- U : jusqu'à (la lettre U vient de l'anglais until de même sens)
- R : release (littéralement « relâcher »)
Une formule de logique des propositions classique, comme la formule (a et b) ou c sur l'ensemble de propositions P = {a, b, c}, associe une valeur de vérité, vrai ou faux, à chaque sous-ensemble de P. Par cette formule exemple, le sous-ensemble {a} (où a a la valeur vrai et b et c ont la valeur faux) rend la formule fausse, le sous-ensemble {b, c} la rend vraie.
Une formule de logique temporelle associe une valeur de vérité non pas à chaque partie de P, mais selon le type de logique, à chaque suite de parties de P ou à chaque arbre sur les parties de P. Une logique définie sur les suites est dite linéaire, tandis qu'une formule définie sur les arbres est dite branching logic ou logique à embranchements.
Prenons le cas des logiques linéaires. Une telle logique associe donc une valeur de vérité, vrai ou faux, à chaque suite telle que chaque soit une partie de P. Notons M une telle formule, nous avons :
Intuitivement, si la suite V représente l'évolution dans le temps des différentes propositions de P, alors :
- X(f) est vraie maintenant si f est vraie à l'étape suivante ;
- F(f) est vraie maintenant si f est vraie à au moins une étape ultérieure y compris maintenant ;
- G(f) est vraie maintenant si f est vraie à toutes les étapes suivantes y compris maintenant ;
- f1 U f2 est vraie si, d'une part, f2 est vraie plus tard ou maintenant et, d'autre part, f1 est vraie (y compris) jusqu'à ce que f2 soit vraie ;
- f1 R f2 est vraie si f2 est vraie (y compris) jusqu'à ce que f1 soit vraie ou si f2 est tout le temps vraie.
On peut noter que les modalités U et R sont duales l'une de l'autre :
Différentes logiques[modifier | modifier le code]
Il existe différentes logiques temporelles, dont :
- CTL*, une logique arborescente ;
- Computation tree logic (en) (CTL), une logique arborescente incluse dans CTL* ;
- Logique temporelle linéaire (LTL), une logique linéaire incluse dans CTL* ;
- Metric Interval Temporal Logic (MITL) qui considère un temps continu et renvoie une valeur booléenne[1] ;
- Signal Temporal Logic (STL) qui considère un temps continu et renvoie une valeur réelle[1]
- Des logiques temporelles pour raisonner sur des intervalles de temps. On peut citer le travail de thèse de B. Moszkowski[2], la logique développée par Halpern et Shoham[3], ainsi que les résultats par Y. Venema[4].
Notes et références[modifier | modifier le code]
- (en) 0. Maler et D. Nickovic, « Monitoring Temporal Properties of Continuous Signals », dans Y. Lakhnech et S. Yovine, Formal Techniques, Modelling and Analysis of Timed and Fault-Tolerant Systems, vol. 3253, Springer Berlin Heidelberg, (ISBN 978-3-540-23167-7, DOI 10.1007/978-3-540-30206-3_12).
- Benjamin Charles Moszkowski, « Reasoning About Digital Circuits », Université Stanford (thèse), Stanford University, (lire en ligne, consulté le )
- Joseph Y. Halpern et Yoav Shoham, « A Propositional Modal Logic of Time Intervals », J. ACM, vol. 38, no 4, , p. 935–962 (ISSN 0004-5411, DOI 10.1145/115234.115351, lire en ligne, consulté le )
- (en) Yde Venema, « Expressiveness and completeness of an interval tense logic. », Notre Dame Journal of Formal Logic, vol. 31, no 4, , p. 529–547 (ISSN 0029-4527 et 1939-0726, DOI 10.1305/ndjfl/1093635589, lire en ligne, consulté le )