Temps d'arrêt

Temps d'impact et temps d'arrêt de trois échantillons de mouvement brownien.

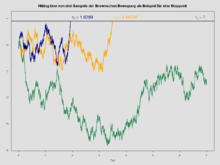
En théorie des probabilités, en particulier dans l'étude des processus stochastiques, un temps d'arrêt (également appelé temps d'arrêt optionnel, et correspondant à un temps de Markov ou moment de Markov défini) est une variable aléatoire dont la valeur est interprétée comme le moment auquel le comportement d'un processus stochastique donné présente un certain intérêt. Un temps d'arrêt est souvent défini par une règle d'arrêt, un mécanisme permettant de décider de poursuivre ou d'arrêter un processus sur la base de la position actuelle et des événements passés.

Ce temps d'arrêt peut être par exemple le moment où un processus stochastique prend fin, ou, dans un processus de Poisson et autres processus de Lévy à accroissements indépendants stationnaires, le moment d'un « saut » incrémental.

Cette notion de temps d'arrêt ne s'appuyant sur aucun évènement futur est étroitement lié à la propriété forte des processus de Markov.

Les temps d'arrêt jouent un rôle important dans la théorie de la décision, et dans les martingales, sont régis par le théorème d'arrêt de Doob (ou théorème d'arrêt optionnel).

Définitions

Définition — Une variable aléatoire $T:\Omega \rightarrow \mathbb {N} \cup \{\infty \}$ est un temps d'arrêt par rapport à une filtration $({\mathcal {F}}_{n})_{n\geq 0}$ si,

$\forall n\in \mathbb {N} ,\quad \{T=n\}\in {\mathcal {F}}_{n},$

ou bien, de manière équivalente, si,

$\forall n\in \mathbb {N} ,\quad \{T\leq n\}\in {\mathcal {F}}_{n}.$

Interprétation

Imaginons que ${\textstyle {\mathcal {F}}_{n}\ }$ désigne ici la tribu engendrée par la suite ${\textstyle (X_{k})_{0\leq k\leq n},\ }$ et que les variables aléatoires ${\textstyle X_{k}\ }$ représentent les résultats d'un joueur lors des parties successives d'un jeu. Dans le cas de variables aléatoires à valeurs dans un espace d'états ${\textstyle E\ }$ fini ou dénombrable, une partie ${\textstyle A\subset \Omega \ }$ appartient à ${\textstyle {\mathcal {F}}_{n}\ }$ si et seulement s'il existe ${\textstyle B\subset E^{n+1}\ }$ tel que

${\begin{aligned}A&=\left\{(X_{0},X_{1},\dots ,X_{n})\in B\right\}\\&=\left\{\omega \in \Omega \ |\ \left(X_{k}(\omega )\right)_{0\leq k\leq n}\in B\right\}.\end{aligned}}$

Supposons que ${\textstyle T\ }$ représente le numéro de la partie après laquelle le joueur décide d'arrêter de jouer : ${\textstyle T\ }$ est donc un temps d'arrêt si et seulement si la décision d'arrêter est prise en fonction des résultats des parties déjà jouées au moment de l'arrêt, i.e. si pour tout ${\textstyle n\ }$ il existe un sous ensemble ${\textstyle B_{n}\subset E^{n+1}\ }$ tel que :

$\{T=n\}\quad \Leftrightarrow \quad \left\{(X_{0},X_{1},\dots ,X_{n})\in B_{n}\right\}.$

L'instant où le joueur s'arrête est donc un temps d'arrêt si la décision d'arrêt ne tient pas compte des résultats des parties futures, donc sous l'hypothèse que don de double-vue et tricherie sont exclus.

Notations

• Soient $(X_{n})_{n}\geq 0\$ une suite de variables aléatoires (un processus stochastique) et T un temps d'arrêt par rapport à une filtration $({\mathcal {F}}_{n})_{n\geq 0}$. Le processus observé au temps T (ou arrêté au temps T) est noté $\ X_{T}(\omega ),\$ et est défini par

${\begin{aligned}X_{T}(\omega )&=X_{T(\omega )}(\omega )\\&=\sum _{n\geq 0}X_{n}(\omega )1\!\!1_{T(\omega )=n}.\end{aligned}}$

Sur l'ensemble $\{\omega \in \Omega \,|\,T(\omega )=+\infty \},\$ la définition de $\ X_{T}(\omega )\$ est problématique : l'ambigüité est de facto levée en posant $\ X_{T}(\omega )=0.\$

• Soit $T\,$ un temps d'arrêt et soit $N\in \mathbb {N} :$
  • $T\wedge N$ est la variable aléatoire définie par $(T\wedge N)(\omega )=\min(T(\omega ),N)\,;$
  • $T\vee N$ est la variable aléatoire définie par $(T\vee N)(\omega )=\max(T(\omega ),N)\,$.

Propriétés

Propriété — Soit $T\,$ un temps d'arrêt, soit $N\in \mathbb {N}$. Alors $S:=T\wedge N,\ S^{\prime }:=T\vee N\$ et $\ S^{\prime \prime }:=T+N\$ sont des temps d'arrêt.

Démonstration

On ne démontrera que le premier point, les deux autres étant semblables :

$\{S=n\}=\{T\wedge N=n\}=\{T=n,n\leq N\}\cup \{n=N,T\geq N\}.$

Or

$\{T=n\}\in {\mathcal {F}}_{n}\ {\text{ et }}\{T\geq N\}=\{T\leq N-1\}^{c}\in {\mathcal {F}}_{N-1}\subset {\mathcal {F}}_{N}.$

Propriété — De même, si $S\ et\ T$ sont des temps d'arrêt, alors $S\wedge T$ en est un.

Définition et propriété — Soit $T\,$ un temps d'arrêt et $A\in {\mathcal {F}}_{\infty }\ :\ A\,$ est appelé évènement antérieur à $T\,$ si:

$\forall n\in \mathbb {N} \ A\cap (T=n)\in {\mathcal {F}}_{n}.$

L'ensemble de ces évènements forme une sous-tribu de ${\mathcal {F}}_{\infty }$ appelée tribu antérieure à $T\,$ et notée ${\mathcal {F}}_{T}.$

Démonstration

• ${\mathcal {F}}_{T}$ contient $\Omega \,$
• ${\mathcal {F}}_{T}$ est stable par réunion dénombrable
• Soit $n\in \mathbb {N}$. On a $A\cap (T=n)\in {\mathcal {F}}_{n}\ et\ (T=n)\in {\mathcal {F}}_{n}.\$ D'où

${\mathcal {F}}_{n}\ni (T=n)\cap (A\cap (T=n))^{c}=(T=n)\cap (A^{c}\cup (T\neq n))$

$=((T=n)\cap A^{c})\cup ((T=n)\cap (T\neq n))=((T=n)\cap A^{c})\cup \emptyset =A^{c}\cap (T=n)$,

et ${\mathcal {F}}_{T}$ est stable par complémentarité.

Proposition — Soient $S\,$ et $T\,$ deux temps d'arrêt tels que $S\leq T$ p.s.. On a alors ${\mathcal {F}}_{S}\subset {\mathcal {F}}_{T}$.

Démonstration

Soit $A\in {\mathcal {F}}_{S}$, c’est-à-dire $\forall n\in \mathbb {N} \ ,\ A\cap (S\leq n)\in {\mathcal {F}}_{n}$. Comme de plus $S\leq T\,$ p.s., $(T\leq n)\subset (S\leq n)$. Par suite,

$A\cap (T\leq n)=A\cap (T\leq n)\cap (S\leq n).$

Or $A\cap (S\leq n)\in {\mathcal {F}}_{n}$ et $(T\leq n)\in {\mathcal {F}}_{n}$ car $T\,$ est un temps d'arrêt. Donc

$A\cap (T\leq n)\in {\mathcal {F}}_{n}.$

Lemme — Soit $Z\,$ une variable aléatoire ${\mathcal {F}}_{\infty }$-mesurable. $Z\,$ est ${\mathcal {F}}_{T}$-mesurable ssi $\forall n\ ,\ 1\!\!1_{(T=n)}\times Z$ est ${\mathcal {F}}_{n}$-mesurable.

Démonstration

Sens réciproque

$Z\,$ est ${\mathcal {F}}_{T}$-mesurable. $(1\!\!1_{(T=n)}\times Z)^{-1}(x)=Z^{-1}(x)\cap (T=n)$ avec $Z^{-1}(x)\in {\mathcal {F}}_{T}.$

Or ${\mathcal {F}}_{T}=\{A\in {\mathcal {F}}_{\infty }/\forall n\ A\cap (T=n)\in {\mathcal {F}}_{n}\}.$

Donc $Z^{-1}(x)\cap (T=n)\in {\mathcal {F}}_{n}.$

Finalement $1\!\!1_{(T=n)}\times Z\,$ est ${\mathcal {F}}_{n}$-mesurable.

Sens direct

$(1\!\!1_{(T=n)}*Z)^{-1}(x)=Z^{-1}(x)\cap (T=n)\in {\mathcal {F}}_{n}$

avec de plus $Z^{-1}(x)\in {\mathcal {F}}_{\infty }$. D'où $Z^{-1}(x)\in {\mathcal {F}}_{T}$ (d'après la définition de ${\mathcal {F}}_{T}$). Donc $Z\,$ est ${\mathcal {F}}_{T}$-mesurable.

Proposition — $X_{T}\,$ est ${\mathcal {F}}_{T}$-mesurable.

Démonstration

${\begin{aligned}X_{T}&=\sum _{n}1\!\!1_{(T=n)}X_{T}+1\!\!1_{(T=\infty )}X_{\infty }\\&=\sum _{n}1\!\!1_{(T=n)}X_{n}+1_{(T=\infty )}X_{\infty }\end{aligned}}$

avec $1\!\!1_{(T=n)}\ et\ X_{n}$ qui sont ${\mathcal {F}}_{n}$-mesurable, d'où $X_{T}\times 1\!\!1_{(T=n)}\,$ est ${\mathcal {F}}_{n}$-mesurable. D'après le lemme précédent, $X_{T}\,$ est ${\mathcal {F}}_{T}$-mesurable.

Exemples et contrexemples

Considérons une suite ${\textstyle X=(X_{k})_{k\geq 0}\ }$ de variable aléatoires, à valeurs dans un ensemble ${\textstyle E,\ }$ et notons ${\textstyle {\mathcal {F}}_{n}\ }$ la tribu engendrée par la suite ${\textstyle (X_{k})_{0\leq k\leq n}.\ }$ Les variables aléatoires ci-dessous sont des temps d'arrêt pour la filtration ${\textstyle ({\mathcal {F}}_{n})_{n\geq 0}}$ :

• Soit ${\textstyle j\ }$ un élément de ${\textstyle E\ }$ ; on appelle instant de premier retour en ${\textstyle j,\ }$ et on note ${\textstyle R_{j},\ }$ la variable aléatoire définie ci-dessous :

$R_{j}=\left\{{\begin{array}{lll}\inf \left\{n>0\,\vert \,X_{n}=j\right\}&&{\textrm {si}}\quad \left\{n>0\,\vert \,X_{n}=j\right\}\neq \emptyset ,\\+\infty &&{\textrm {sinon.}}\end{array}}\right.$

• De même pour ${\textstyle C\ }$ une partie de ${\textstyle E,\ }$ on appelle instant de première entrée dans ${\textstyle C,\ }$ et on note ${\textstyle T_{C},\ }$ la variable aléatoire ci-dessous définie :

$T_{C}=\left\{{\begin{array}{lll}\inf \left\{n\geq 0\,\vert \,X_{n}\in C\right\}&&{\textrm {si}}\quad \left\{n\geq 0\,\vert \,X_{n}\in C\right\}\neq \emptyset ,\\+\infty &&{\textrm {sinon.}}\end{array}}\right.$

• L'instant de ${\textstyle k}$-ème retour en ${\textstyle i,\ }$ noté ${\textstyle R_{i}^{(k)}\ }$ et défini par récurrence par :

$R_{i}^{(k)}=\left\{{\begin{array}{lll}\inf \left\{n>R_{i}^{(k-1)}\,\vert \,X_{n}=i\right\}&&{\textrm {si}}\quad \left\{n>R_{i}^{(k)}\,\vert \,X_{n}=i\right\}\neq \emptyset ,\\+\infty &&{\textrm {sinon.}}\end{array}}\right.,$

ou encore l'instant de ${\textstyle k}$-ème entrée dans ${\textstyle C,\ }$ sont des temps d'arrêt.

• Pour ${\textstyle i\ }$ et ${\textstyle j\ }$ dans ${\textstyle E,\ }$ on pose ${\textstyle T=\inf \left\{n\geq 0\,\vert \,X_{n}=i{\text{ et }}X_{n+1}=j\right\}.\ }$ On peut montrer que ${\textstyle T\ }$ n'est pas un temps d'arrêt, mais que, par contre, ${\textstyle T+1\ }$ est un temps d'arrêt.

Articles connexes

• Problème du secrétaire