Transformée Mojette
La transformée Mojette est une application de la géométrie discrète. Plus précisément, c’est une version discrète exacte[Quoi ?] de la transformée de Radon (Théorème de Radon). Le premier travail de discrétisation de la transformée de Radon a été réalisé par Myron Katz en 1978[1]. Depuis 1994, cette transformée a été développée par le laboratoire IRCCyN – UMR CNRS 6597 devenu LS2N à Nantes.
La première caractéristique de la transformée Mojette est de n’utiliser que des additions et des soustractions. De plus, celle-ci est redondante. La transformée utilise la géométrie discrète pour répartir l'information sur un support de géométrie discrète. Puis, sur ce support, on projette l'opérateur Mojette dans les directions discrètes partageant l'information sur les projections. Quand le nombre de projections est suffisant, l'information initiale peut être reconstruite. La transformée Mojette a déjà été utilisée dans de nombreux domaines d'application dans les problématiques du traitement du signal.
Les principaux domaines d’investigation sont :
- Le stockage distribué sur disques ou réseau
- L’envoi de paquets sur les réseaux
- La tomographie médicale
- Le tatouage d’images et le chiffrement d’images
Historique[modifier | modifier le code]
Après un an de recherche, la première communication introduisant la « Transformée Mojette » a eu lieu en mai 1995 dans la première édition du congrès national « CORESA » au CCETT de Rennes. Elle sera suivie par de nombreuses publications dans le monde entier. En 2011, le livre "The Mojette transform: theory and applications" chez ISTE-WILEY fut bien reçu par la communauté scientifique. Tout cela a encouragé les enseignants-chercheurs de l’IRCCyN à continuer le travail de recherche sur ce sujet.
Jean-Pierre Guédon, Professeur des Universités et concepteur de la transformée, la nomme la «Transformée Mojette ». Le mot « Mojette » vient du nom des haricots blancs en Vendée, écrit initialement « Moghette ou Mojhette». Dans de nombreux pays, le haricot sec est donc un outil pédagogique de base représentant une unité exacte qui permet d'apprendre l'addition simplement et visuellement. Le choix du nom « Mojette » permet donc de souligner le fait que la transformée n’use que d'addition ou soustraction entières. Il est intéressant de voir que depuis longtemps, les mojettes servent à compter.
Un dicton vendéen dit qu'il faut savoir "compter ses mojettes" c'est-à-dire son argent. Dans le monde anglo-saxon, on parle aussi de "bean counter" ce qui représente le petit fonctionnaire non zélé qui fait les additions. Une vieille expression anglaise dit "he knows how many beans make five ", ce qui veut dire : "il connait son affaire" et qui se réfère à une personne qui est férue de puzzles mathématiques. Cette expression provient des temps des abaques anglaises où les haricots servaient à noter les incréments dans les calculs.
L’objectif original de la « Transformée Mojette » était de créer un outil de mathématique discret qui permette de diviser le plan de Fourier en secteur angulaire et radial. La première tentative d’application fut l’encodage de l’image psychovisuelle reproduisant le canal de la vision humaine. Cependant, elle ne fut jamais réalisée.
Mathématiques[modifier | modifier le code]
La définition "brute" de la transformée Mojette est celle-ci :
La figure 1 suivante permet d'expliciter en partie la transformée.

On part de la fonction f(k,l) représentée par les 16 pixels p1 à p16. Ces valeurs possibles de la fonction au point (k,l) différent selon les applications. Cela peut être une valeur binaire 0 ou 1 comme souvent utilisés pour différencier le fond et la forme. Cela peut être une valeur ternaire comme dans le jeu Mojette. Cela peut être également un ensemble fini de valeurs entières entre 0 et (n-1), ou souvent on prend un ensemble de cardinal égal à une puissance de 2 ou bien un nombre premier. Mais cela peut encore être les entiers ou les réels avec un nombre infini de possibilités, même si cette dernière idée ne sera quasiment jamais exploitée.
Avec les indices "k" comme "kolonne" et "l" comme "ligne", on définit un repère cartésien. Mais ici nous n'aurons besoin que des coordonnées entières. En rouge sur la figure 2, on voit que l'on a choisi arbitrairement le point bas gauche comme origine (position 0,0) et le sens des 2 axes. Dans chaque pixel est noté en rouge ses coordonnées.
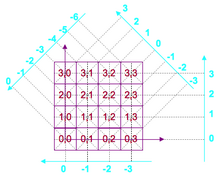
Pour les projections, le système de coordonnées est donné par celui de la grille. En effet, on respecte 2 impératifs :
- le pixel (0,0) se projette toujours sur le point 0 de la projection (cela provient de la linéarité de l'opérateur Mojette)
- le sens de la projection est fixé "anti-horaire" comme en trigonométrie lorsque l'on va de 0° à 180°.
Cela donne donc nécessairement les positions des bins comme écrit en bleu sur la figure 2. La correspondance est avec la formule (1) : les points rouges correspondent à l'indice (k,l) et les points bleus à l'indice b. Donc il ne reste que les valeurs (p,q) à éclaircir pour avoir tous les éléments de la transformée.
Ces 2 valeurs (p,q) sont précisément celles qui caractérisent la transformée Mojette. Elles définissent l'angle de projection. La figure 3 montre des flèches de couleur correspondant chacune (par le code de couleur) à la projection indexée par (p,q). Pour l'angle 90°, la projection est représentée en dessous de la grille pour plus de commodités mais la direction est bien montante. Le tableau 1 fait la correspondance entre les angles en degrés et les valeurs de p et q.

| 0° | p=1 | q=0 | b-l=0 |
| 45° | p=1 | q=1 | b+k-l=0 |
| 90° | p=0 | q=1 | b+k=0 |
| 135° | p=-1 | q=1 | b+k+l=0 |
Tableau 1 : les correspondances d'angles de projections avec l'équation de direction b + qk - pl = 0
Les seuls angles valides en Mojette sont donnés par les règles suivantes :
1) un angle est donné par la direction de projection en ligne et colonne
2) une direction est composée de deux entiers (p,q) avec pgcd(p,q)=1
3) un angle est toujours compris entre 0 et 180° ce qui veut dire que q n'est jamais négatif
Ces règles permettent d'avoir une unicité dans la correspondance d'un angle. Par exemple, pour 45°, la règle 2 interdit de définir l'angle par les couples (2,2) ou (3,3) et la règle 3 interdit d'utiliser (-2,-2) ou (-1,-1). Seul l'angle (p=1,q=1) répond à la fois aux 3 règles.
Applications & Réalisations[modifier | modifier le code]
Le stockage distribué sur disques ou réseau[modifier | modifier le code]
Le domaine d’application le plus important utilisant la « Transformée Mojette » est le stockage distribué sur disques ou sur réseaux. Aujourd’hui, le stockage « Mojette » permet d’augmenter par 2 l’espace de stockage disponible (ou de façon équivalente, une réduction de 50 % des coûts d’équipements pour un volume donné à stocker), d’entretien et d’énergie par rapport aux technologies actuelles.
En 2010, Pierre Évenou, ingénieur de recherche de l’équipe IVC au laboratoire IRCCyN, décide de créer la start-up Fizians (aujourd'hui renommée Rozo Systems) qui développe le logiciel RozoFS. Il s'agit d'un logiciel libre qui offre un système de fichiers distribués. La distribution de ces données repose sur le transformée Mojette afin d'apporter de la protection aux données ainsi qu'aux applications qui y accèdent. Il s'agit d'utiliser les propriétés de la transformée Mojette comme code d'effacement. Plusieurs applications émanent de cette technique telles que le Cloud Computing et Cloud Storage, la virtualisation des serveurs de stockage ou encore l’archivage des données.
L’envoi de paquet sur les réseaux[modifier | modifier le code]
Grâce à la redondance de la transformée, l’envoi de paquet peut être fragmenté sans risque de perte. En parallèle, la propriété de n’utiliser que des additions et des soustractions permet d’augmenter la vitesse de transmission des informations. Enfin, l’information ne pouvant être reconstruite qu’en ayant l’angle original des projections, elle apporte aussi une sécurisation des données.
Cette application a été retenue par Thales Cholet pour ses réseaux ad hoc (sans fil et en utilisant les terminaux pour transmettre les messages entre eux) afin de le sécuriser et d'avoir plusieurs chemins entre la source et la destination. En 2002, la start-up PIBI a utilisé cette technologie pour proposer des services de paiement sécurisé sur Internet.
La tomographie médicale[modifier | modifier le code]
Dans le domaine de l’imagerie médicale, les propriétés de la « Transformée Mojette » permettent de créer un mapping direct et de résoudre le problème du calcul des angles. Cependant, l’acquisition de l’image utilisant la transformée Mojette n’a pas été encore développé. La problématique d’obtenir des valeurs exactes en utilisant des acquisitions de données qui ne sont qu’approximatifs a été étudiée mais doivent être continué. Par contre, le post-traitement des images médicales est opérationnel car l’acquisition des données est déjà faite.
Ces résultats sont utilisés par les sociétés Keosys en 2001 par Jérôme Fortineau et Qualiformed créée en 2006 par Stéphane Beaumont. Le Pr. Guédon et le laboratoire IRCCyN ont été fortement impliqués dans la création de ces entreprises. Ils ont permis de financer déjà plusieurs thèses et participé à des projets de recherche continuant à développer l’application en tomographie médicale. Les résultats ont permis de déposer des brevets et de les implémenter sur leurs équipements de traitement d’images.
Le tatouage d’images et le chiffrement d’images[modifier | modifier le code]
La cryptographie et le watermarking ont fait aussi partie des recherches effectuées au laboratoire IRCCyN pour développer les applications de la transformée. Elle apporte des solutions pour la sécurisation et l’authentification.
En cryptographie, l’instabilité de la transformée Mojette permet de sécuriser les données. Le fait que la transformée soit exacte permet de chiffrer les informations et ne permet aucun écart même minime. En tatouage d’image, la transformée est très efficace en fingerprinting. En insérant des marques « Transformée Mojette » sur image, on peut authentifier les documents en utilisant les mêmes propriétés qu’en cryptographie.
Bibliographie[modifier | modifier le code]
- Myron Bernard Katz, Questions of Uniqueness and resolution in reconstruction from projections. Vol. 26. Lecture Notes in Biomathematics, Springer 1978.
- Jeanpierre Guédon, N. Normand, B. Parrein, and C. Pouliquen, “Distributed image transmission and storage on Internet system,” in ACIDCA, 2000, p. 164–169.
- B. Parrein, N. Normand, and J. Guédon, “Multiple description coding using exact discrete Radon transform,” in IEEE Data Compression Conference, 2001, p. 508.
- J. Guédon, N. Normand, P. Verbert, B. Parrein, F. Autrusseau, “Load-balancing and scalable multimedia distribution using the Mojette transform,” in Internet Multimedia Management Systems II, ITCOM, 2001, p. 226–234.
- J. Guédon, B. Parrein, N. Normand,, “Internet Distributed Image Information System,” Integrated Computer-Aided Engineering, vol. 8, no. 3, p. 205–214, .
- B. Parrein, “Description multiple de l’information par transformation Mojette,” Université de Nantes, 2008.
- F. Autrusseau and J. Guédon, “Image watermarking for copyright protection and data hiding via the Mojette transform,” in Security and Watermarking of Multimedia Contents IV, 2002, p. 378–386.
- F. Autrusseau and J. Guédon, “Image Watermarking in the Fourier Domain Using the Mojette Transform,” in Digital Signal Processing, 2002, p. 725–728.
- F. Autrusseau, “Modélisation Psychovisuelle pour le tatouage des images,” Université de Nantes, 2011.
- F. Autrusseau and J. Guédon, “A joint multiple description-encryption image algorithm,” in International Conference on Image Processing, 2003, p. 269–272.
- J. Guédon, N. Normand, and B. Parrein, “Multimedia packet transport: multiple layers or descriptions?,” in IEEE Packet Video workshop, 2003, p. 7 p.
- B. Parrein, N. Normand, and J. Guédon, “Multimedia forward error correcting codes for wireless LAN,” Annales des Télécommunications, vol. 58, no. 3–4, p. 448–463, Jul. 2008.
- F. Autrusseau and J. Guédon, “Chiffrement Mojette d’images médicales,” Ingénierie des Systèmes d’Information (ISI), vol. 8, no. 1, p. 113–134, .
- O. Déforges, M. Babel, N. Normand, B. Parrein, J. Ronsin, J, and L. Bédat, “Le LAR aux Mojettes,” in CORESA 04 - COmpression et REprésentation des Signaux Audiovisuels, 2004, p. 165–168.
- P. Verbert, V. Ricordel, J. Guédon, and P. Verbert, “Analysis of Mojette transform projections for an efficient coding,” in Workshop on Image Analysis for Multimedia Interactive Services (WIAMIS, 2004, p. -.
- M. Babel, B. Parrein, O. Déforges, N. Normand, J. Guédon, and J. Ronsin, “Secured and progressive transmission of compressed images on the Internet: application to telemedicine,” in SPIE 17th Annual Symposium / Electonic Imaging - Internet Imaging, 2005, p. 126–136.
- J. Guédon and N. Normand, “The Mojette Transform: The First Ten Years,” in Discrete Geometry for Computer Imagery, 2005, vol. 3429, p. 79–91.
- M. Servières, N. Normand, J. Guédon, and Y. Bizais, “The Mojette Transform: Discrete Angles for Tomography,” in Discrete Tomography and its Applications, 2005, vol. 20, p. 587–606.
- M. Servieres, “Reconstruction Tomographique Mojette,” Université de Nantes; École Centrale de Nantes, 2009.
- F. Autrusseau, P. Evenou, and T. Hamon, “Secure Distributed Storage based on the Mojette transform,” in Nouvelles technologies de la répartition, 2006, p. 161–170.
- F. Autrusseau, B. Parrein, and M. Servieres, “Lossless Compression Based on a Discrete and Exact Radon Transform: A Preliminary Study,” in International Conference on Acoustics, Speech and Signal Processing, 2006, p. 425–428.
- [21] M. Kalantari, F. Jung, G. Moreau, and J. Guédon, “Détection entièrement automatique de points de fuite dans des scènes architecturales urbaines,” in CORESA 2006 COmpression et REprésentation des Signaux Audiovisuels, 2006, p. 41–46.
- M. Servières, N. Normand, and J. Guédon, “Interpolation method for the Mojette Transform,” in Medical Imaging 2006: Physics of Medical Imaging, 2006, vol. 6142, p. 61424I.
- N. Normand, A. Kingston, and P. Évenou, “A Geometry Driven Reconstruction Algorithm for the Mojette Transform,” in Discrete Geometry for Computer Imagery, 2006, vol. 4245, p. 122–133.
- S. Hamma, E. Cizeron, H. Issaka, and J. Guédon, “Performance evaluation of reactive and proactive routing protocol in IEEE 802.11 ad hoc network,” in ITCom 06 - next generation and sensor networks, 2008, p. 638709.
- A. Kingston, S. Colosimo, P. Campisi, and F. Autrusseau, “Lossless Image Compression and Selective Encryption Using a Discrete Radon Transform,” in International Conference on Image Processing, 2007, p. 465–468.
- A. Daurat and N. Normand, “Transformation et reconstruction par projections,” in Géométrie discrète et images numériques, A. M. David Coeurjolly, Ed. Hermès, 2008, p. 239–251.
- N. Normand and J. Guédon, “Applications de la transformation Mojette,” in Géométrie discrète et images numériques, A. M. David Coeurjolly, Ed. Hermès, 2008, p. 337–347.
- B. Parrein, F. Boulos, P. Le Callet, and J. Guédon, “Priority image and video encoding transmission based on a discrete Radon transform,” in IEEE Packet Video 2007, 2007, p. 6 pages.
- S. Chandra, I. Svalbe, and J. Guédon, “An exact, non-iterative Mojette inversion technique utilising ghosts,” in 14th IAPR international conference on Discrete geometry for computer imagery, 2008, p. .
- H. Fayad, J. Guédon, I. Svalbe, N. Normand, and Y. Bizais, “Mojette and FRT tomographs,” in Medical Imaging 2008, 2008, vol. 6913, p. -.
- H. Fayad, J. Guédon, I. Svalbe, Y. Bizais, and N. Normand, “Applying Mojette discrete Radon transforms to classical tomographic data,” in Medical Imaging, 2008, vol. 6913, p. 69132S.
- A. Kingston and F. Autrusseau, “Lossless Image Compression via Predictive Coding of Discrete Radon Projections,” Signal Processing Image Communication, vol. 23, no. 4, p. 313–324, Jun. 2008.
- M. Babel, B. Parrein, O. Déforges, N. Normand, J. Guédon, and V. Coat, “Joint source-channel coding: secured and progressive transmission of compressed medical images on the Internet,” Computerized Medical Imaging and Graphics, vol. 32, no. 4, p. 258–269, Apr. 2008.
- A. Kingston, B. Parrein, and F. Autrusseau, “Redundant Image Representation via Multi-Scale Digital Radon Projection,” in International Conf. of Image Processing, 2008, p. 2069.
- P. Jia, J. Dong, L. Qi, and F. Autrusseau, “Directionality Measurement and Illumination Estimation of 3D Surface Textures by Using Mojette Transform,” in 19th International Conference on Pattern Recognition, 2010, p. 1144.
- D. Coeurjolly and N. Normand, “Discrete geometry and projections (chap 1),” in The Mojette Transform: Theory and Applications, jeanpierre Guédon, Ed. iste & wiley, 2009, p. 15 pages.
- J. Guédon and N. Normand, “Reconstructability with the inverse Mojette transform (chap 4),” in The Mojette Transform: Theory and Applications, jeanpierre Guédon, Ed. iste & wiley, 2009, p. 15 pages.
- J. Guédon and N. Normand, “Direct Mojette transform (chap 3),” in The Mojette Transform: Theory and Applications, jeanpierre Guédon, Ed. iste & wiley, 2009, p. 23 pages.
- A. Kingston and F. Autrusseau, “Lossless compression (chap 9),” in The Mojette transform: Theory and Applications, jeanpierre Guédon, Ed. iste & wiley, 2009, p. 19 pages.
- A. Kingston, F. Autrusseau, E. Grall, T. Hamon, and B. Parrein, “Mojette based security (chap 10),” in The Mojette transform: Theory and Applications, J. Guédon, Ed. iste & wiley, 2009, p. 25 pages.
- A. Kingston, F. Autrusseau, and B. Parrein, “Multiresolution Mojette transform (chap 6),” in The Mojette transform: Theory and Applications, J. Guédon, Ed. iste & wiley, 2009, p. 29 pages.
- N. Normand, I. Svalbe, P. Evenou, and A. Kingston, “Inverse Mojette transform algorithms (chap 5),” in The Mojette Transform: Theory and Applications, J. Guédon, Ed. iste & wiley, 2009, p. 25 pages.
- B. Parrein, F. Boulos, N. Normand, and P. Evenou, “Communication, networks and storage (chap 7),” in The Mojette Transform: Theory and Applications, J. Guédon, Ed. iste & wiley, 2009, p. 29 pages.
- M. Servières, J. Guédon, N. Normand, and Y. Bizais, “Mojette discrete tomography (chap 8),” in The Mojette Transform: Theory and Applications, J. Guédon, Ed. iste & wiley, 2009, p. 29 pages.
- I. Svalbe and J. Guédon, “Discrete versions of the Radon Transform (chap 2),” in The Mojette Transform: Theory and Applications, J. Guédon, Ed. iste & wiley, 2009, p. 17 pages.
- C. Zhang, J. Dong, J. Li, and F. Autrusseau, “A New Information Hiding Method for Image Watermarking Based on Mojette Transform,” in Second International Symposium on Networking and Network Security, 2010, p. 124–128.
- N. Normand, I. Svalbe, B. Parrein, and A. Kingston, “Erasure Coding with the Finite Radon Transform,” in Wireless Communications & Networking Conference, 2010, p. 1–6.
- S. S. Chandra, N. Normand, A. Kingston, J. Guédon, and I. Svalbe, “Fast Mojette Transform for Discrete Tomography,” 13-Jul-2012.
- C. Liu, and J. Guédon, “The 2 and 3 materials scene reconstructed from some line Mojette projections,” in IEEE IPTA Conference, 2010, p. 6.
- C. Liu, J. Guédon, I. Svalbe, and Y. Amouriq, “Line Mojette ternary reconstructions and ghosts,” in IWCIA, 2011, p. 11.
- C. Liu and J. Guédon, “The limited material scenes reconstructed by line Mojette algorithms,” in Franco-chinese conference, 2011, p. 2.
- J. Dong, L. Su, Y. Zhang, F. Autrusseau, and Y. Zhanbin, “Estimating Illumination Direction of 3D Surface Texture Based on Active Basis and Mojette Transform,” Journal of Electronic Imaging, vol. 21, no. 013023, p. 28 pages, Apr. 2012.
- D. Pertin, G. D’Ippolito, N. Normand, and B. Parrein, “Spatial Implementation for Erasure Coding by Finite Radon Transform,” in International Symposium on signal, Image, Video and Communication 2012, 2012, p. 1–4.
- S. Chandra, I. Svalbe, J. Guedon, A. Kingston, and N. Normand, “Recovering Missing Slices of the Discrete Fourier Transform using Ghosts,” IEEE Transactions on Image Processing, vol. 21, no. 10, p. 4431–4441, Jul. 2012.
- H. Der Sarkissian, Jp. Guédon, P. Tervé, N. Normand and I. Svalbe. (2012)." Evaluation of Discrete Angles Rotation Degradation for Myocardial Perfusion Imaging", EANM Annual Congress 2012.
- C. Liu and J. Guédon, “Finding all solutions of the 3 materials problem,” in proceedings of SIFWICT, 2013, p. 6.
- B. Recur, H. Der Sarkissian, Jp. Guédon and I.Svalbe, "Tomosynthèse à l’aide de transformées discrètes", in Proceeding TAIMA 2013
- H. Der Sarkissian, B. Recur, N. Normand and Jp. Guédon, "Mojette space Transformations", in proceedings of SWIFCT 2013.
- B. Recur, H. Der Sarkissian, M. Servières, N.Normand, Jp. Guédon, "Validation of Mojette Reconstruction from Radon Acquisitions" in Proceedings of 2013 IEEE International Conference on Image Processing.
- H. Der Sarkissian, B. Recur, N. Normand, Jp.Guédon. (2013), "Rotations in the Mojette Space" in 2013 IEEE International Conference on Image Processing.
Références[modifier | modifier le code]
- Myron Bernard Katz, Questions of Uniqueness and resolution in reconstruction from projections. Vol. 26. Lecture Notes in Biomathematics, Springer 1978.
Liens externes[modifier | modifier le code]
- HAL : HAL est l'archive ouverte pluridisciplinaire du CNRS destinée au dépôt et à la diffusion d'articles scientifiques de niveau recherche, publiés ou non, et de thèses. Toutes les publications citées ci-dessous sont accessibles sur HAL.
- La Mojette sauce calculs : article de Presse-Océan expliquant l'origine du nom mojette de cette transformée
- Jeu en ligne: version ludique de la transformée MOJETTE
- Site officiel de Rozo Systems
- Page communautaire GitHub du logiciel RozoFS






