Réluctance
La réluctance, ou résistance magnétique, est une grandeur physique qui caractérise l'aptitude d'un circuit magnétique à s'opposer à sa pénétration par un champ magnétique[1],[2].
Le nom de cette grandeur a été créé par analogie avec celui de la résistance (électrique)[1].
L'inverse de la réluctance est appelé perméance magnétique[3].
Analogie d'Hopkinson[modifier | modifier le code]
Principes[modifier | modifier le code]
Cette analogie consiste à faire un parallèle entre les circuits électriques et les circuits magnétiques.
| Circuits électriques | Circuits magnétiques |
|---|---|
| Intensité du courant électrique | Flux du champ magnétique dans le circuit |
| Résistance | Réluctance |
| Conductance | Perméance |
| Conductivité | Perméabilité magnétique étant la perméabilité relative |
| Force électromotrice | Force magnétomotrice ou |
| Loi d'Ohm | Loi d'Hopkinson |
Remarque : saturation[modifier | modifier le code]
Cette analogie peut permettre de prévoir le comportement d'un circuit, soit en statique, soit en alternatif, dans le cas bien précis de la linéarité perméabilité constante, soit totale linéarité entre champ et induction magnétique. Dans les cas où ces conditions ne sont pas totalement remplies, il peut être possible d'étendre la notion de réluctance.
En effet, la valeur de perméabilité est susceptible de varier en fonction de divers paramètres du problème considéré, même dans un cas simple.
La variation de la valeur de perméabilité peut trouver son origine dans la saturation pour les forts champs magnétiques, ce qui correspond à la saturation des courbes d’hystérésis B-H (voir cycle d'hystérésis).
En statique, cet effet de saturation peut être pris en compte par introduction de zones ayant une perméabilité plus faible aux endroits où se produit la saturation. Cependant, en signal alternatif, la saturation n'a lieu que pour certaines fractions du cycle. La notion de réluctance devient alors difficile à manipuler.
Par ailleurs, la perméabilité est susceptible de varier aux hautes fréquences. La variation de perméabilité en fonction de la fréquence dépend des matériaux (capacité des domaines à suivre le champ magnétique extérieur) et de leurs géométries (lamination des matériaux magnétiques conducteurs par des isolants afin de minimiser les courants de Foucault, par exemple).
Détermination de la réluctance d'un circuit magnétique homogène[modifier | modifier le code]
Cas général[modifier | modifier le code]
Pour un circuit magnétique homogène, c’est-à-dire constitué d'un seul matériau et de section homogène, il existe une relation permettant de calculer sa réluctance en fonction du matériau qui le constitue et de ses dimensions[1] :
- en H-1,
- étant la perméabilité magnétique en kg⋅m⋅A-2⋅s-2 (ou henrys par mètre, symbole : H⋅m-1 ou H/m),
- la longueur en mètres,
- la section en mètres carrés.
Réluctance équivalente d'un entrefer[modifier | modifier le code]
La réluctance d'un entrefer de faible épaisseur est donnée par[1] :
- ,
avec :
- l'épaisseur de l'entrefer,
- la perméabilité du vide,
- la section de l'entrefer.
Si l'épaisseur de l'entrefer est grande, il n'est plus possible de considérer que les lignes de champ magnétique restent perpendiculaires à l'entrefer. On doit alors tenir compte de l'épanouissement du champ magnétique c'est-à-dire considérer que la section S est plus grande que celle des pièces métalliques de part et d'autre de l'entrefer[1].
Réluctance d'un circuit magnétique de forme complexe[modifier | modifier le code]
Principe du calcul[modifier | modifier le code]
Les lois d'association des réluctances permettent de calculer celle d'un circuit magnétique de forme complexe ou composé de matériaux aux caractéristiques magnétiques différentes. On décompose ce circuit en tronçons homogènes, c'est-à-dire de même section et constitués du même matériau.
- Association en série : Lorsque deux tronçons homogènes ayant respectivement pour réluctance et se succèdent, la réluctance de l'ensemble est .
- Association en parallèle : Lorsque deux tronçons homogènes ayant respectivement pour réluctance et sont placés côte à côte, la réluctance de l'ensemble est telle que , soit encore .
À l'aide de ces lois on peut calculer la réluctance du circuit magnétique complexe dans son intégralité[1].
Exemple[modifier | modifier le code]
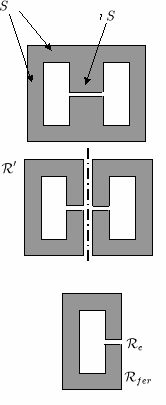
Les circuits magnétiques de la même forme que celui représenté ci-contre sont fréquemment utilisés pour réaliser des transformateurs d'alimentation à découpage. Le bobinage est réalisé dans la fenêtre et entoure le noyau central. Pour calculer sa réluctance, on commence par considérer qu'il est constitué de deux circuits magnétiques de forme simple accolés l'un contre l'autre, donc en parallèle. On peut alors écrire :
- .
Le circuit magnétique de réluctance est lui-même constitué de l'association en série de deux tronçons homogènes : la partie en matériau ferromagnétique et l'entrefer. On a donc :
- .
La réluctance recherchée est donc égale à :
- .
Fréquemment, le terme est très grand devant le terme . La réluctance du circuit est alors pratiquement égale à la réluctance de l'entrefer.
Représentation d'un aimant permanent[modifier | modifier le code]
En toute rigueur, un aimant permanent est un élément fortement non linéaire, interdisant l'utilisation du modèle de réluctance. Il est cependant possible de l'étendre en introduisant un circuit inducteur, sous réserve de la connaissance de la courbe d’hystérésis de l'aimant dans la direction considérée, et de l'appréciation de l'excursion de champ considérée (invalide si l'excursion se rapproche du champ coercitif).
Un aimant de longueur , de section , de pente de droite de recul et d'induction rémanente se représente par :
- un matériau de réluctance ,
- un circuit inducteur .
Relation entre réluctance et inductance[modifier | modifier le code]
Une formule relie l'inductance d'un enroulement réalisé autour d'un circuit magnétique, la réluctance de ce circuit magnétique et le nombre de spires de l'enroulement :
- , avec
- l'inductance de l'enroulement en H,
- le nombre de spires de l'enroulement, sans unité.
Notes et références[modifier | modifier le code]
- J.C Duez, G. Auclerc, Électronique appliquée 2, Paris, Classiques Hachette, 1973 ; 2e éd. 1975, 304 p. (ISBN 2010029801 et 978-2010029806), p. 62-66.
- Réluctance, sur le site cnrtl.fr, consulté le 21 février 2015.
- Marcel Jufer, Traité d'électricité – Électromécanique, vol. 9, Lausanne, Presses polytechniques et universitaires romandes, coll. « Traité d'électricité de l'École polytechnique fédérale de Lausanne », , 3e éd. (1re éd. 1995), 384 p. (ISBN 978-2-88074-285-0, lire en ligne), p. 8-11 et suiv.








































