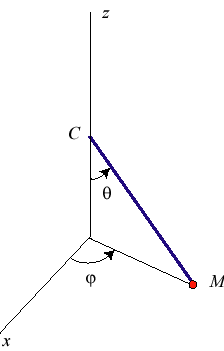
Pendule sphérique
On appelle pendule sphérique un dispositif formé d'une tige de masse nulle de longueur accrochée à un point fixe et à laquelle est fixée à l'autre extrémité une masse , habilité à se mouvoir en 3 dimensions, et placé dans un champ de pesanteur uniforme. En bref, c'est un pendule simple en 3D.
Mais le problème peut aussi être considéré comme un cas particulier de mouvement d'un point matériel astreint à glisser sans frottement sur une surface, en l'occurrence la sphère de centre et de rayon .
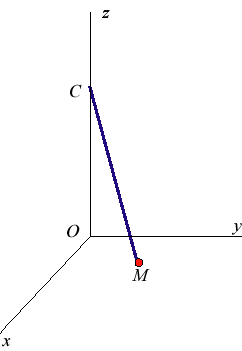
Petites oscillations : pendule de Hooke[modifier | modifier le code]
|
La relation fondamentale de la dynamique s'écrit :
On peut considérer pour de petites oscillations que le point reste dans le plan et que donc , ce qui donne l'équation approchée des petites oscillations : Le mouvement est donc celui d'un point matériel dans un champ central où la force est proportionnelle à la distance au centre (champ dit harmonique). L'équation différentielle approchée s'intègre en : ; Les trajectoires sont donc les ellipses de centre , dites ellipses de Hooke. La période du mouvement est une constante égale à , la même que celle des petites oscillations du pendule simple plan. |
Remarquons que ce cas représente celui d'un pendule dont la tige pourrait s'allonger de sorte que reste dans un plan perpendiculaire à l'axe (ceci alors pour des oscillations quelconques).
Augmentation des oscillations[modifier | modifier le code]

|
Si l'on augmente l'amplitude du mouvement de Hooke, on voit l'ellipse de Hooke précesser comme sur la figure ci-contre.
Ce mouvement de précession est largement plus grand, si l'on n'y prend garde, que la précession de Foucault due au pivotement terrestre sidéral. Cela est très souvent la raison pour laquelle l'expérience de Foucault échoue. |
Mise en équation utilisant l'approche newtonienne[modifier | modifier le code]
Mise en équation utilisant l'approche lagrangienne[modifier | modifier le code]
Pour des variations infinitésimales et , on a deux écarts perpendiculaires et . Les deux composantes perpendiculaires de la vitesse sont donc et et l'énergie cinétique vaut . L'énergie potentielle valant , la fonction de Lagrange s'écrit :
Le lagrangien, a priori fonction de ne dépend ici explicitement ni de ni de . On a ,
et , ce qui conduit aux deux équations de Lagrange : et .
On retrouve bien les équations (4) et (5).
Cas du pendule conique[modifier | modifier le code]
Une trajectoire possible est celle d'un parallèle : on parle alors de pendule conique, dont la théorie a été faite par Huygens. En écrivant dans l'équation (4) que l'angle , appelé angle de nutation, est constant, on obtient la vitesse de rotation autour de l'axe, appelée vitesse de précession : , qui est donc constante. On constate que ne peut dépasser 90° ; la période du mouvement est .
Au voisinage de ce mouvement, il existe des mouvements avec une petite nutation.
Cas général[modifier | modifier le code]
Il est intégrable à une quadrature près, puisque la surface a pour axe de révolution la verticale.
L'équation (5) s'intègre en (6) ; la vitesse de rotation autour de l'axe est donc minimale à l'équateur et augmente en se rapprochant des pôles.
L'équation (4) s'intègre alors en (7) ; redonnant bien le cas du pendule plan.
En posant , (7) devient :
.
Voir des vues de différentes trajectoires sur le site : courbe du pendule sphérique.
Généralisations[modifier | modifier le code]
- Dans le cas précédent, on a implicitement supposé que le référentiel était galiléen ; dans le cas général, il faut rajouter la force d'inertie d'entraînement, et la force d'inertie complémentaire, ou force de Coriolis ; le cas du pendule de Foucault est celui des petites oscillations d'un tel pendule, avec une rotation d'axe vertical, et une force d'inertie d'entraînement négligeable..
- Si le pendule possède une inertie de rotation, et est en rotation sur lui-même, on obtient la toupie, ou le gyroscope.
- Comme pour le pendule plan, on peut considérer un pendule double, voire multiple.
Source[modifier | modifier le code]
Paul Appell : traité de mécanique rationnelle, page 530 à 541