Paradoxe de Cramer

Représentation graphique du paradoxe : les courbes sont du 3^e degré et le nombre d'intersections est de 9.

En mathématiques, et plus précisément en géométrie algébrique, le paradoxe de Cramer (nommé d'après Gabriel Cramer, mais qui avait déjà été remarqué par Maclaurin) affirme que le nombre de points d'intersection de deux courbes de haut degré peut être supérieur au nombre de points nécessaires pour définir l'une de ces courbes. Le paradoxe résulte de deux théorèmes : le théorème de Bézout, montrant que le nombre de points d'intersection des deux courbes est égal au produit de leurs degrés, et un théorème énoncé par Cramer, affirmant qu'une courbe de degré n est déterminée par n(n + 3)/2 points ; dès que n est égal ou supérieur à 3, ces deux valeurs sont apparemment contradictoires.

Nombre de points déterminant une courbe

Une courbe algébrique de degré n (ou moins) peut être représentée (dans un repère affine) par une équation cartésienne de la forme

$\sum _{k=0,k+p\leq n}^{n}a_{k,p}x^{k}y^{p}=0$

où l'on voit qu'il y a 3 coefficients pour les termes de degré 2, 4 coefficients pour ceux de degré 3, etc. ; on en déduit aisément (voir nombre triangulaire) qu'il y a au total (n+1)(n+2)/2 coefficients, et, puisque deux équations proportionnelles définissent la même courbe, que celle-ci est en définitive déterminée par n(n+3)/2 coefficients indépendants.

Si on se donne alors p points (x_i,y_i) (avec 1 ≤ i ≤ p) les courbes passant par ces points sont celles satisfaisant au système des p équations :

$\sum _{k=0,k+p\leq n}^{n}a_{k,p}x_{i}^{k}y_{i}^{p}=0$

lequel possède des solutions non nulles tant que p < (n+1)(n+2)/2. Ainsi, les droites (correspondant à n=1) sont déterminées par deux points distincts et les coniques (correspondant à n=2) le sont par cinq points, puisque 5 = 2×(2+3)/2.

Le paradoxe de Cramer : cubiques et quartiques

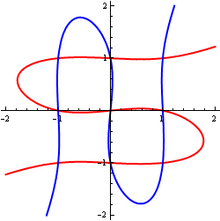
Dans un échange de lettres avec Euler, Cramer a développé les calculs précédents dans le cas des cubiques et des quartiques (les courbes de degré 4), montrant qu'une cubique est déterminée par 9 points et une quartique par 14. Remarquant ensuite que deux cubiques se coupent en 9 points et deux quartiques en 16 (ce sont des cas particuliers du théorème de Bézout, lequel affirme que deux courbes de degrés m et p se coupent en général en mp points), il s'étonne de la contradiction : neuf points arbitraires définissent en effet une cubique unique, et, en général, puisque 14 points arbitraires définissent une quartique unique, il n'est pas possible d'en faire passer une (et encore moins plusieurs) par 16 points quelconques.

Résolution du paradoxe

À la suite de cette correspondance, Euler a publié une analyse du paradoxe, montrant que les points d'intersection ne sont pas en réalité quelconques, et plus précisément que le système d'équations mentionné plus haut n'est pas, dans le cas de ces points, formé d'équations indépendantes. Il fallut cependant attendre le travail de Julius Plücker pour que soit donné une résolution complète du paradoxe, utilisant la notion de rang du système : dans le cas de points d'intersection de deux courbes de degré n, ce rang est d < n², et donc si d des points d'intersection sont donnés, les autres peuvent être déterminés.

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Cramer's paradox » (voir la liste des auteurs).

• (en) Eric W. Weisstein, « Cramer-Euler Paradox », sur MathWorld

Liens externes

• (en) Ed Sandifer "Cramer’s Paradox"