Loi d'Amdahl
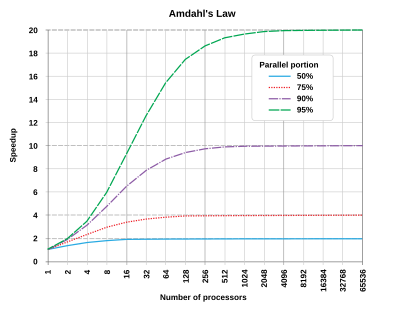
En architecture informatique, la loi d'Amdahl donne l'accélération théorique en latence de l'exécution d'une tâche à charge d'exécution constante que l'on peut attendre d'un système dont on améliore les ressources. Elle est énoncée par l'informaticien Gene Amdahl à l'AFIPS Spring Joint Computer Conference en 1967.
La loi d'Amdahl peut être formulée de la façon suivante :
où
- Slatence est l'accélération théorique en latence de l'exécution de toute la tâche ;
- s est le nombre de fils d'exécutions (threads) utilisés pour exécuter la tâche
- p est le pourcentage du temps d'exécution de toute la tâche concernant la partie bénéficiant de l'amélioration des ressources du système avant l'amélioration.
De plus,
montrent que l'accélération théorique de l'exécution de toute la tâche augmente avec l'amélioration des ressources du système et que, quelle que soit l'amélioration, l'accélération théorique est toujours limitée par la partie de la tâche qui ne peut tirer profit de l'amélioration.
La loi d'Amdahl est souvent utilisée en calcul parallèle pour prédire l'accélération théorique lors de l'utilisation de plusieurs processeurs. Par exemple, si un programme a besoin de 20 heures d'exécution sur un processeur uni-cœur et qu'une partie du programme qui requiert une heure d'exécution ne peut pas être parallélisée, même si les 19 heures (p = 95 %) d'exécution restantes peuvent être parallélisées, quel que soit le nombre de processeurs utilisés pour l'exécution parallèle du programme, le temps d'exécution minimal ne pourra passer sous cette heure critique. Ainsi, l'accélération théorique est limitée au plus à 20 (1/(1 − p) = 20).
On en déduit deux règles : premièrement, lors de l'écriture d'un programme parallèle, il faut limiter autant que possible la partie sérielle ; deuxièmement, un ordinateur parallèle doit être un excellent ordinateur sériel pour traiter le plus rapidement possible la partie sérielle.
Démonstration[modifier | modifier le code]
Une tâche exécutée par un système dont les ressources sont améliorées par rapport à un système similaire initial peut être séparée en deux parties :
- une partie ne bénéficiant pas de l'amélioration des ressources du système ;
- une partie bénéficiant de l'amélioration des ressources du système.
Exemple. — Un programme informatique qui traite les fichiers d'un disque. Une partie du programme commence par lire le répertoire du disque et créer une liste de fichiers en mémoire. Puis une autre partie du programme passe chaque fichier à un fil d'exécution pour traitement. La partie qui lit le répertoire et crée la liste de fichiers ne peut pas être accélérée sur un ordinateur parallèle, mais la partie qui traite les fichiers peut l'être.
Le temps d'exécution de toute la tâche avant l'amélioration des ressources est noté T. Il inclut le temps d'exécution de la partie ne bénéficiant pas de l'amélioration des ressources et le temps d'exécution de celle en bénéficiant. Le pourcentage du temps d'exécution de toute la tâche concernant la partie bénéficiant de l'amélioration des ressources avant l'amélioration des ressources est noté p. Celui concernant la partie n'en bénéficiant pas est donc 1 − p. Il vient
C'est l'exécution de la partie bénéficiant de l'amélioration des ressources qui est accélérée d'un facteur s après l'amélioration des ressources. Par conséquent, le temps d'exécution de la partie n'en bénéficiant pas reste identique, tandis que celui de la partie en bénéficiant devient
Le temps d'exécution théorique T(s) de toute la tâche après l'amélioration des ressources est ainsi
La loi d'Amdahl exprime l'accélération théorique en latence de l'exécution de toute la tâche à charge d'exécution constante C, ce qui donne
Estimation de p[modifier | modifier le code]
p peut être estimé à partir de l'accélération mesurée Slatence(s) = T/T(s) de toute la tâche par un système amélioré possédant une accélération spécifique s de l'exécution de la partie de la tâche bénéficiant de l'amélioration du système, en utilisant
Estimé de cette façon, p peut être utilisé dans la loi d'Amdahl pour prédire l'accélération théorique pour une accélération s quelconque de l'exécution de la partie de la tâche bénéficiant de l'amélioration du système.
Un rendement parfois décevant[modifier | modifier le code]
- Certaines applications comme le traitement d'image tirent un très bon parti du parallélisme. Dans leur cas, p peut se retrouver voisin de 95 %.
- D'autres comme l'analyse numérique pourront tirer profit d'un changement d'algorithme (par exemple le remplacement d'une méthode de Gauss-Seidel par une méthode de Jacobi qui converge plus lentement, mais est totalement parallélisable).
Les autres cas se montrent décevants : pour p = 50 %, le passage à un biprocesseur fait gagner 25 % de temps. Le passage à 12 processeurs fait passer ce gain de temps à 46 %.
Note. — La loi d'Amdahl est considérée ici dans le cas d'un système où tous les processeurs sont consacrés au même utilisateur, et à des threads du même processus. Ce cas ne se rencontre pas toujours. Dans la pratique, les résultats seront bien plus mauvais encore si l'on ne gère pas l'affinité processeur qui veille à ce que les mêmes processeurs reprennent dans la mesure du possible les mêmes processus, afin d'éviter des rechargements intempestifs de cache.
Augmentation de p[modifier | modifier le code]
Un cas où p se retrouve évidemment voisin de 100 % est celui où les processeurs exécutent des programmes différents : étant indépendants, ils sont ipso facto parallélisables, et de surcroît sans le moindre effort à entreprendre pour assurer cette parallélisation. Les problèmes restent à ce stade que :
- le temps écoulé pour une application donnée n'est pas directement réduit : une simulation de quatre heures continuera à faire attendre quatre heures ses résultats (mais sera moins ralentie par les autres processus si elle revendique qu'un processeur lui soit dédié en propre) ;
- l'antémémoire et le cache disque se retrouvent plus encombrés de données appartenant à des processus différents, et il faut prévoir leur augmentation de taille en conséquence. Le problème disparaît pour l'antémémoire lorsque celle-ci se trouve sur le microprocesseur lui-même, ce qui règle du même coup les effets d'échelle.
Autre loi d'Amdahl[modifier | modifier le code]
Une loi plus ancienne d'Amdahl concernait un équilibre observé empiriquement dans les ordinateurs : « Une instruction par seconde requiert un octet de mémoire et un bit par seconde de capacité d'entrée–sortie. » De fait, cette loi semble être restée valable assez longtemps (100 MIPS, 100 Mo de mémoire vive et 100 Mb/s s'observaient vers 2000 et les réseaux gigabit ont commencé à se répandre à peu près en même temps que les mémoires de 1 Go).
Limitations[modifier | modifier le code]
La loi d'Amdahl est très gênante pour le parallélisme. Elle indique que la performance d'un système ne dépend pas seulement du nombre de ressources mises en parallèle et de surcroît, elle désigne la partie sérielle comme le facteur limitant. Et la limite est sévère car il est très difficile de paralléliser 90 % d'un programme. La loi de Gustafson modère les conclusions de la loi d'Amdahl.
Références[modifier | modifier le code]
- (en) Gene Amdahl, Validity of the Single Processor Approach to Achieving Large-Scale Computing Capabilities, AFIPS Conference Proceedings, (30), p. 483-485, 1967.
- (en) John L. Hennessy et David A. Paterson, Computer Architecture: A Quantitative Approach, 2nd edition, 1996, p. 29-32. (ISBN 1-55860-329-8)
- [PDF] (en) Mark D. Hill, Michael R. Marty, « Amdahl’s Law in the Multicore Era »







