Canon rythmique

En musique, un canon rythmique est analogue à un canon traditionnel (superposition à elle-même, mais en décalage, d'une phrase musicale donnée). La seule différence est que les hauteurs des notes ne sont pas prises en compte mais seulement leur durée (seul le rythme est répété, pas la mélodie elle-même).

Si la construction d'un canon rythmique est relativement simple, celle-ci devient plus compliquée si l'on impose comme contrainte supplémentaire que les attaques des notes par les différentes voix ne doivent jamais coïncider dans le temps. Ce type de canon rythmique, principalement étudié par Dan Tudor Vuza, donne lieu à un développement mathématique faisant intervenir la théorie des groupes.

Définition, historique

La notion de canon est ancienne en musique. L'étude spécifique de la théorie des canons rythmiques, qui se focalise sur les seuls rythmes en ignorant hauteurs, timbres et autres paramètres du son, a été vraiment initiée par Dan Tudor Vuza dans les années 1980.

Le principe du canon est simple, plusieurs voix jouent un même motif mais décalé dans le temps. Pour un canon rythmique on peut formaliser une voix par la suite des instants où une note est jouée, $A=(a_{1},a_{2}...a_{n})$. On a affaire à un canon si toutes les voix sont translatées l'une de l'autre: $A'=(a'_{1},a'_{2}...a'_{n})=A+b$. Si on note $B=(b_{1},b_{2}...b_{n})$ l'ensemble des décalages, les différentes voix sont les $b_{i}+(a_{1},a_{2}...a_{n})$. A est le motif et B constitue les entrées.

Bien entendu on peut faire des canons rythmiques sans autre contrainte; le problème devient intéressant quand on exige que les voix ne se recouvrent pas, i.e. que la somme $A+B$ soit directe, i.e. encore qu'il n'y ait pas plus d'une note par instant. C'est encore plus contraignant si on exige exactement une note, ni plus ni moins, par instant. On retrouve alors un problème de pavage (ou mosaïque).

Différents théorèmes techniques établissent qu'un canon qui pave tous les instants possibles avec un motif fini est nécessairement périodique, et qu'un canon possède nécessairement une unité de temps commune. On est donc ramené mathématiquement parlant à la question d'un pavage de l'ensemble Z des entiers relatifs de la forme $\mathbf {Z} =A+B+n\mathbf {Z}$ ou encore, passant au quotient modulo la période n du canon, $\mathbf {Z} /n\mathbf {Z} =A\oplus B$.

Exemple: Pour $A=\{0,1,3,6\}$ on peut prendre $n=12$ et $B=\{0,4,8\}$. En effet, $A\oplus B=\{0,1,3,4,5,6,7,8,9,10,11,14\}$ et 14 se réduit à 2 modulo 12.

le motif 0136 et ses deux décalages de 4 et 8 pavant modulo 12.

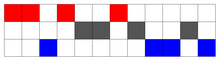
Vuza s'est intéressé particulièrement aux cas où ni A, ni B ne possèdent de période propre, qu'il appelle RCMC (Rhythmic Canon of Maximal Category) et que les chercheurs suivants ont plutôt appelé "canons Vuza". Il s'avère que les résultats retrouvés par Vuza à ce propos sont équivalents à une difficile classification des groupes cycliques étudiée par plusieurs mathématiciens depuis les années 1950 et achevée par Sands.

Résultats mathématiques

Théorèmes fondamentaux

Le cas des pavages sans modulo de la tranche d'entiers de 0 à $n-1$ est trivial et réglé par un théorème de De Bruijn.

Le théorème fondamental qui établit la périodicité des canons rythmiques de motif fini remonte aux années 1950, on en a des démonstrations un peu sommaires par Hajos et De Bruijn.

Théorème de périodicité: si A est une partie finie de $\mathbf {Z}$ qui pave, c'est-à-dire qu'il existe un "supplémentaire" C tel que $A\oplus C=\mathbf {Z}$, alors C est périodique: il existe un entier naturel n tel que $C=n\mathbf {Z} \oplus B$ et donc $A\oplus B=\mathbf {Z} /n\mathbf {Z}$en réduisant modulo n.

Il s'agit donc d'un cas particulier de décomposition en somme directe d'un groupe fini. Hajòs a conjecturé que dans ce cas (groupe cyclique), l'un des deux facteurs A, B est nécessairement périodique, au sens où il existe une période $0<p<n$ telle que, par exemple, $A+p=A\mod n$. Il a obligeamment fourni le premier contre-exemple à sa propre conjecture, pour $n=108$.

Plus précisément, on peut classer les groupes cycliques en bons et mauvais groupes, selon qu'ils admettent ou non des pavages apériodiques. Divers auteurs ont contribué à l'étude de ce problème pendant les années 1950 et 1960, jusqu'à ce que Sands achève la classification des décompositions en sommes directes des groupes finis abéliens. Dans le cas des groupes cycliques, le résultat est le suivant:

Théorème (Sands & alii): $\mathbf {Z} /n\mathbf {Z}$ est un ``bon groupe ", c'est-à-dire que toute factorisation $\mathbf {Z} /n\mathbf {Z} =A\oplus B$admet un facteur périodique, si et seulement si n a l'une des cinq formes suivantes (où p, q, r, s désignent des nombres premiers distincts):

$n=p^{\alpha }\qquad n=p^{\alpha }q\qquad n=p^{2}q^{2}\qquad n=p^{2}qr\qquad n=pqrs$

Ce résultat a été retrouvé par D.T. Vuza indépendamment entre 1980 et 1990. On constate que le plus petit groupe cyclique qui soit mauvais est $\mathbf {Z} /72\mathbf {Z}$.

Il est clair que translater A ou B ne change pas le fait qu'ils réalisent un canon rythmique. Il en est de même pour l'échange des facteurs A et B, ou pour l'inversion (changer A en -A). Cela permet de les réduire tous deux à des formes canoniques, ce qui réduit le nombre de cas dans les listes exhaustives. Ainsi pour $n=72$, pour des canons rythmiques apériodiques (canons de Vuza) il y a essentiellement 6 cas pour A et 3 pour B, comme par exemple $A=\{0,1,4,7,13,24,28,37,43,48,49,52\}{\text{ et }}B=\{0,8,16,18,26,34\}$.

Autres transformations

En partant d'un canon rythmique $A\oplus B=\mathbf {Z} /n\mathbf {Z}$ on a mentionné qu'il est possible d'en déduire d'autres. Il est non trivial qu'on peut remplacer A (ou B) par l'une des transformées affines:

Théorème: si c est premier avec n, alors $cA\oplus B=\mathbf {Z} /n\mathbf {Z}$.

Exemple: on a vu que le motif $A=\{0,1,3,6\}$ pave modulo 12; il en est de même pour $7A=\{0,7,21,42\}=\{0,6,7,9\}$ et avec le même B.

Il existe plusieurs démonstrations de cette propriété fondamentale, la première est probablement celle de Vuza. On peut voir qu'elle équivaut en un sens à l'irréductibilité des polynômes cyclotomiques rationnels.

Il est possible de changer la taille d'un canon pour en produire un plus grand.

Exemple: en partant du motif $A=\{0,1,3,6\}$ qui pave $\mathbf {Z} /8\mathbf {Z} {\text{ avec }}B=\{0,4\}$, on peut fabriquer un nouveau motif en faisant ``bégayer'' A, qui deviendrait $A'=2A\cup (2A+1)=\{0,2,6,12\}\cup \{1,3,7,13\}=\{0,1,2,3,6,7,12,13\}$ qui pave $\mathbf {Z} /16\mathbf {Z}$ avec $B'=\{0,8\}$. Plus général encore, on peut remplacer l'une des augmentations de A par un autre motif qui pave aussi avec B, par exemple

$2\{0,1,2,3\}\cup (2A+1)=\{0,2,4,6\}\cup \{1,3,7,13\}=\{0,1,2,3,4,6,7,13\}$

Canon multiplexé

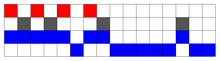
On peut y voir une forme de multiplexage.

La concaténation est une opération encore plus simple qui permet de doubler, tripler… la longueur d'un canon.

Par exemple on prolonge $A=\{0,1,3,6\}\mod 8$ en $A*A=\{0,1,3,6,8,9,11,14\}$

Perturbations

En partant de canons réguliers, simples, plusieurs chercheurs ont développé des perturbations qui conservent la somme directe mais rendent les facteurs apériodiques. Szabò comme Kolountzakis, par exemple, utilisent des sommes directes de progressions arithmétiques bien choisies, qu'ils perturbent en ajoutant un élément de A à certains éléments de B. Les canons ainsi constitués étant très grands (période au moins 900), l'intérêt de ces constructions est surtout théorique.

Formulation polynômiale

Initialement, la modélisation la plus fructueuse du problème a pris la forme suivante:

Traduction polynômiale: pour une partie finie A d'entiers naturels on note $A(X)=\sum _{a\in A}X^{a}$ son polynôme caractéristique. Alors on a l'équivalence $A\oplus B=\mathbf {Z} /n\mathbf {Z} \Leftrightarrow A(X)\times B(X)=1+X+X^{2}+\dots X^{n-1}\mod X^{n}-1$

Comme le polynôme du second membre a pour facteurs les polynômes cyclotomiques d'indice divisant n, on peut utiliser les outils de la théorie de Galois des corps cyclotomiques.

Les diverses transformations mentionnées dans la section précédente ont des traductions algébriques très simples dans ce contexte.

Au XXIe siècle, on utilise plutôt la

Formulation sous transformée de Fourier discrète

Si on considère deux parties A, B de $\mathbf {Z} /n\mathbf {Z}$, on peut définir leurs transformées de Fourier discrètes par les coefficients complexes $a_{k}=\sum _{x\in A}e^{-2i\pi xk/n}$ (des variantes sont possibles). Alors on a le critère

Caractérisation par DFT: A pave $\mathbf {Z} /n\mathbf {Z}$ avec B, autrement dit $A\oplus B=\mathbf {Z} /n\mathbf {Z}$, si et seulement si

$a_{0}b_{0}=|A||B|=n$ et pour $k=1,2\dots n-1$, $a_{k}{\text{ ou }}b_{k}$ est nul.

Cela résulte du théorème sur la transformée de Fourier d'un produit de convolution. Il permet de se ramener aux (complémentaires des) supports des DFT, qui ont des géométries très particulières liées aux conditions de Coven et Meyerowitz.

Il est facile d'échanger les deux caractérisations précédentes en remarquant que les coefficients de Fourier sont des valeurs particulières du polynôme caractéristique.

Développements récents

Dénombrements

Fripertinger a été le premier à donner des dénombrements des canons rythmiques pavant $\mathbf {Z} /n\mathbf {Z}$ pour des petites valeurs de n (moins de 144). L'existence de canons de Vuza compliquant la donne, il a fallu développer de nouvelles techniques pour énoncer exhaustivement ces derniers. Actuellement on sait les trouver tous quand n ne dépasse pas quelques milliers. Il n'existe pas de procédé connu permettant de trouver tous les canons rythmiques de taille donnée en un temps raisonnable.

Canons avec variantes du motif

Pavage avec le motif 014 et une augmentation (en bleu)

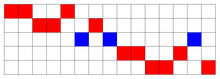
• Un canon est dit par augmentation (resp. par diminution) si le thème est répété en valeurs rythmiques plus longues (resp. plus courtes) que dans l'original : par exemple des blanches au lieu de noires (resp. par exemple des croches au lieu de noires). Il est plus facile de paver si on s'autorise à utiliser des augmentations du motif, ainsi $A=\{0,1,4\}$ ne pave pas avec ses décalages mais on peut paver l'intervalle d'entiers entre 0 et 14 avec $A{\text{ et }}2A=\{0,2,8\}.$ On ne sait pas si tout motif (fini) pave avec un nombre fini d'augmentations.

• La rétrogradation d'un motif permet aussi plus de souplesse. Par exemple, $A=\{0,1,3\}$ ne permet pas de paver (par translations) mais avec son rétrogradé on a le pavage $\{0,1,3\}\cup \{2,4,5\}=\{0,1,2,3,4,5\}$. Il a été démontré qu'un tel pavage existe pour tout motif de trois éléments. Il existe des motifs qui ne pavent pas même avec leur rétrogradé, comme $\{0,1,3,4\}$.

Canons modulo p

L'équation polynômiale traduisant la condition de pavage de $\mathbb {Z} /n\mathbb {Z}$ est écrite dans l'anneau quotient $\mathbb {Z} [X]/(X^{n}-1)$. Comme en arithmétique, on peut se poser la question de considérer les coefficients (entiers) modulo un nombre premier quelconque, p.

Il se trouve que contrairement à la question du pavage de Z, le pavage est inconditionnel sous cette forme:

Théorème (pavage modulo p):

Pour toute partie A d'entiers et tout premier p, il existe un ``complément" B et un entier n tel que

$A(X)\times B(X)=1+X+X^{2}+\dots +X^{n-1}\mod (X^{n}-1,p)$

Pavage modulo 2 avec le motif 013

Cette condition signifie musicalement que le nombre de notes sur chaque temps est 1 ou 1+p ou 1+2p ou… Par exemple pour p=2 on relaxe la condition de pavage à celle d'avoir un nombre impair de notes.

Certains résultats ont été obtenus sur ces canons modulo p, notamment quant à l'optimalité de l'algorithme glouton et la taille du pavage minimal pour certains motifs simples.