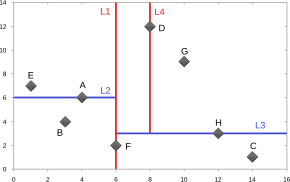
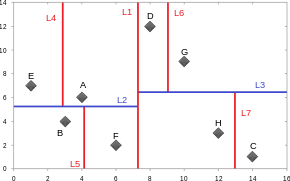
Arbre kd

En informatique, un arbre k-d (ou k-d tree, pour k-dimensional tree) est une structure de données de partition de l'espace permettant de stocker des points, et de faire des recherches (recherche par plage, plus proche voisin, etc.) plus rapidement qu'en parcourant linéairement le tableau de points. Les arbres k-d sont des cas particuliers d'arbres BSP (binary space partition trees).
Cette structure a été proposée par Jon Louis Bentley de l'Université Stanford en 1975[1].
Description
[modifier | modifier le code]Les arbres k-d sont des arbres binaires, dans lesquels chaque nœud contient un point en dimension k. Chaque nœud non terminal divise l'espace en deux demi-espaces. Les points situés dans chacun des deux demi-espaces sont stockés dans les branches gauche et droite du nœud courant. Par exemple, si un nœud donné divise l'espace selon un plan normal à la direction (Ox), tous les points de coordonnée x inférieure à la coordonnée du point associé au nœud seront stockés dans la branche gauche du nœud. De manière similaire, les points de coordonnée x supérieure à celle du point considéré seront stockés dans la branche droite du nœud.
Construction
[modifier | modifier le code]Il y a plusieurs possibilités de construction d'arbres k-d. La construction standard se fait en suivant ces deux conditions :
- la direction de l'hyperplan est choisie en fonction de la hauteur du point dans l'arbre ; pour un arbre k-d en dimension 3, le plan de la racine sera par exemple normal au vecteur (1,0,0), le plan des deux enfants sera normal au vecteur (0,1,0), celui des petits-enfants sera normal au vecteur (0,0,1), puis à nouveau normal au vecteur (1,0,0), et ainsi de suite…
- afin d'avoir un arbre équilibré, le point inséré dans l'arbre à chaque étape est celui qui a la coordonnée médiane dans la direction considérée.
La contrainte sur la sélection du point médian n'est pas une obligation, mais permet de s'assurer que l'arbre sera équilibré. Le tri des points à chaque étape a un coût en temps, ce qui peut amener à un temps de création de l'arbre assez long. Il est possible de prendre la médiane d'un nombre fixé de points choisis aléatoirement pour le prochain point à insérer, ce qui donne en général un arbre globalement équilibré.
À partir d'une liste de n points, l'algorithme suivant construit un arbre k-d équilibré :
fonction kdtree(listePoints, profondeur)
si la liste listePoints est vide
retourner l'arbre vide
// Sélectionne l'axe de comparaison en fonction de la profondeur du nœud
axe := profondeur mod k;
// trie la liste de points et sélectionne le point médian
sélectionner pointMédian selon l'axe dans la liste listePoints
// Crée le nœud courant, et construit récursivement les deux fils
nœud := nouveau nœud
nœud.point := pointMédian;
node.filsGauche := kdtree(points dans listePoints avant pointMédian, profondeur+1);
node.filsDroit := kdtree(points dans listePoints après pointMédian, profondeur+1);
return node;
La complexité algorithmique de construction d'un arbre k-d est de O(n log2 n) si un algorithme médian de complexité O(n log n) est utilisé. Si on utilise un algorithme de calcul de la médiane de complexité linéaire (en O(n)), alors la construction de l'arbre a une complexité en O(n log n).
Le choix de la méthode de sélection de l'hyperplan de coupe a une grande influence sur l'efficacité de l'algorithme de recherche du plus proche voisin[2]. La méthode standard présentée ci-dessus (utilisation du point médian) peut donner des cellules très minces selon une dimension ; lors d'une recherche de plus proche voisin, on peut donc avoir de nombreuses cellules dans la boule de recherche[3], ce qui oblige à visiter de nombreuses branches de l'arbre. Si à l'inverse on utilise le point milieu (milieu géométrique, l'hyperplan coupant l'hypercube en deux parties égales), on obtient des cellules « épaisses », c'est-à-dire dont le rapport entre la dimension la plus grande et la plus petite est au pire de 2:1, la boule de recherche recouvre donc un nombre limité de cellules ; mais de nombreuses cellules peuvent être vides, ce qui amène à effectuer des recherches dans des zones vides.
Maneewongvatana et Mount[2] proposent la méthode du point milieu glissant, qui peut générer des cellules minces, mais entourées de cellules grasses, et aucune cellule vide ; il garantit donc une bonne efficacité de l'algorithme de recherche. Cette méthode consiste à prendre en première intention le point milieu ; si tous les points se trouvent du même côté de l'hyperplan (donc si une cellule est vide), on fait glisser le point générant l'hyperplan jusqu'à rencontrer un point de l'ensemble. Une cellule contient alors au moins un point. L'arbre ainsi généré n'est pas nécessairement équilibré.
Alternative
[modifier | modifier le code]On peut également construire un arbre k-d dans lequel les points sont les feuilles de l'arbre[4].
Notes et références
[modifier | modifier le code]- (en) J. L. Bentley, « Multidimensional binary search trees used for associative searching », Communications of the ACM, vol. 18, no 9, , p. 509-517 (DOI 10.1145/361002.361007)
- (en) Songrit Maneewongvatana et David M. Mount, « It's okay to be skinny, if your friends are fat », 4th Annual CGC Workshop on Computational Geometry, (lire en ligne [PDF])
- Pour un point et un rayon donnés, et pour une norme Lm choisie, la boule de recherche est l'ensemble des points vérifiant ; si m = 2 (norme euclidienne), la boule de recherche est l'hypersphère
- (en) « Orthogonal Range Searching », Computational Geometry, Springer, , p. 95-120 (ISBN 978-3-540-77973-5 et 978-3-540-77974-2, DOI 10.1007/978-3-540-77974-2_5)