Arbre cousu
En algorithmique, un arbre cousu, ou threaded tree en anglais[1], est une structure de données, basée sur un arbre binaire.
Principe[modifier | modifier le code]
Coudre un arbre binaire revient à :
- parcourir cet arbre en parcours préfixe, postfixe ou infixe ;
- dans le cadre de ce parcours, lier le fils droit de chaque feuille (originellement, il s'agit de ) à son successeur.
Il est nécessaire de matérialiser les nouvelles liaisons de manière différente des liaisons père-fils de l'arbre de départ. Dans le cas contraire, la figure ne serait plus un arbre (présence de cycles).
Types[modifier | modifier le code]
D'une manière générale, on dénombre trois sortes d'arbre cousus :
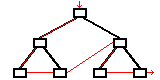
Arbre cousu en préordre[modifier | modifier le code]
Un arbre dont le chaînage suit un parcours préfixe de l'arbre : nœuds parents en premier, nœuds enfants ensuite.
Arbre cousu en postordre[modifier | modifier le code]
Un arbre dont le chaînage suit un parcours postfixe de l'arbre : nœuds enfants en premier, nœuds parents en dernier.
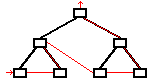
Arbre cousu en inordre[modifier | modifier le code]
Un arbre dont le chaînage suit un parcours infixe de l'arbre : nœud fils gauche, nœud parent, nœud fils droit.
Dans le cas d'un arbre binaire de recherche, ce chaînage correspond à une liste chaînée triée.
Historique[modifier | modifier le code]
Le concept d'arbre cousu est dû à Joseph Morris qui le publia en 1979[2].
Notes et références[modifier | modifier le code]
- Une référence pour la traduction en français : « Cours d'algorithmique », sur polypolytech.
- Joseph M. Morris, « Traversing binary trees simply and cheaply », Information Processing Letters, Elsevier, vol. 9, no 5, , p. 197-200
Lien externe[modifier | modifier le code]
- K. R. Kaplan, « Threaded Search Trees », sur Université Rutgers.