Antisymétrie (linguistique)
L'antisymétrie de la syntaxe est une théorie linguistique développée par Richard Kayne qui s'inscrit dans la lignée du courant générativiste. Kayne propose un « axiome de correspondance linéaire » grâce auquel il est possible de dériver la structure syntaxique et l'ordre des mots d'une langue.
Concepts
[modifier | modifier le code]Tous les concepts développés ci-après sont exclusivement tirés de l'œuvre de Kayne[1].
L'ordre linéaire
[modifier | modifier le code]Kayne se base sur les propriétés mathématiques d'un ordre linéaire. Pour que ce dernier soit obtenu à partir d'un ensemble d'éléments ordonnés entre eux il faut trouver les propriétés suivantes :
- Transitif donc si <x;y> et <y;z> alors <x;z>. Si on se le représente sous forme de frise, c'est plus clair : x | y | z. Ici x est à gauche de y et y est à gauche de z, il faut donc que x soit à gauche de z sinon ce n'est pas transitif.
- Total pour tout x,y,z il faut qu'un ordre soit précisé entre chaque. Si on reprend la frise : Si je sais seulement que x est à gauche de y et x à gauche de z, je ne sais pas quelle est la relation entre y et z et je ne sais donc pas où les placer exactement.
- Antisymétrique il ne faut pas trouver <x;y> et <y;x> qui sont deux ordres symétriques de la même paire d'éléments. On ne peut pas les placer en frise.
À partir de ces observations mathématiques, Kayne décide d'appliquer ce concept aux mots et à leur organisation dans une phrase (en effet, les phrases sont linéaires puisqu'elles sont prononcées dans le temps[2]). On peut résumer les principes vus plus haut ainsi: pour qu’une phrase soit linéarisable, il ne faut pas qu’il existe d’ambiguïtés : donc il faut que tous les mots se voient attribuer un ordre (total), il faut que cet ordre soit cohérent, qu’il permette une continuité (transitivité) et il ne faut pas qu’un ordre différent soit attribué aux mêmes éléments (antisymétrie).
Le vocabulaire de la LCA
[modifier | modifier le code]- Non-terminaux : Il s'agit des nœuds (par opposition aux mots) de la structure syntaxique.
- Non-head : Les nœuds qui dominent d'autres nœuds.
- Head : Les nœuds qui dominent des terminaux.
- Terminaux : Les mots, ce qu'on cherche à linéariser.
- D : la relation de dominance qu'entretiennent les non-terminaux entre eux dans la structure.
- d : la relation de dominance entre non-terminaux et terminaux dans la structure.
- d(X) : L'image de X via d= les terminaux que X domine.
- A : l'ensemble des paires de non-terminaux tels que le premier c-commande asymétriquement le second.
- T : l'ensemble des terminaux.
La C-commande asymétrique
[modifier | modifier le code]Un Nœud X en c-commande asymétriquement un second Y ssi :

- X c-commande Y et Y ne c-commande pas X.
- X et Y sont des catégories.
- Aucun segment de X ne domine Y.
- Les catégories qui dominent X dominent également Y.
Ici on peut voir que B C-commande C et C c-commande B. B c-commande également E mais E ne c-commande pas B. Donc B c-commande asymétriquement E.
La LCA
[modifier | modifier le code]« d(A) is a linear ordering of T. [1] »
Cette définition implique que c'est la structure des non-terminaux (l'arbre syntaxique) qui devra respecter les propriétés antisymétriques. L'obtention d'une structure antisymétrique permettra d'obtenir l'ordre linéaire des mots (terminaux) que cette structure domine.
Calcul
[modifier | modifier le code]Pour un arbre avec les caractéristiques suivantes : X c-commande asymétriquement Y et Z. Y c-commande asymétriquement Z. d(X)={à,la,maison}, d(Y)={la,maison}, d(Z)={maison}.
Il est nécessaire de dériver tout d'abord A, l'ensemble des paires dont le premier membre c-commande asymétriquement le second. On obtient ainsi A={<X;Y>,<Y;Z>,<X;Z>}.
On dérive ensuite d(A)={d(<X;Y>),d(<Y;Z>),d(<X;Z>)}= {<à;la>;<la;maison>;<à;maison>} ={à,la,maison} Cet ordre est bien linéaire puisqu'il est transitif, total (chaque terminal est mis en relation avec les autres), et antisymétrique.
Implications
[modifier | modifier le code]Le schéma X-barre
[modifier | modifier le code]La LCA dérive une partie du schéma X-barre car, pour être asymétriques, les arbres syntaxiques doivent respecter les contraintes suivantes : deux heads ne peuvent être sœurs/compléments, deux non-heads ne peuvent être sœurs/compléments. Seules une "head" et une "non-head" peuvent être sœurs. Le résultat obtenu ressemble à un schéma X-barre sans la position de spécifieur.
La position de spécifieur ne peut être obtenu que via adjonction. Ainsi le niveau X' disparaît. On a maintenant la structure XP → XP → X → x (le petit x étant un terminal). La raison est simple, les principes de l'asymétrie font que le seul moyen d'obtenir un arbre correct lorsqu'il y a un spécifieur est de rendre possible l'exclusion de c-commande entre le niveau XP et l'autre niveau XP (autrefois X'). Pour cela il faut postuler qu'il n'y a qu'un seul XP (l'ancien X'), et que le second, au-dessus, n'est qu'un adjoint, un segment de XP. Ainsi, le XP le plus haut ne peut pas C-commander le moindre élément puisqu'il ne répond pas à la définition de la c-commande asymétrique (voir plus haut). Une autre conséquence de l'antisymétrie est qu'il n'est désormais possible de n'avoir qu'un adjoint et qu'un complément par projection fonctionnelle.

L'ordre des mots
[modifier | modifier le code]Avec les principes de la LCA, seuls les ordres de mots présentant une opposition entre la position du spécifieur et celle du complément peuvent être dérivés. On obtient ainsi comme ordres de mots S-H-C (ou SVO) si on décide d'organiser les paires dans A comme énoncé plus haut(i.e. le premier membre c-commande asymétriquement le second) ou C-H-S (OVS) si on prend l'organisation inverse. Kayne remarque que l'ordre SVO étant beaucoup plus représenté parmi les langues mondiales[3] que OVS, le premier sera plus probable en tant qu'universel.
Mais et les autres langues?
[modifier | modifier le code]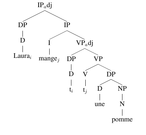
L'ordre SVO permet de dériver la structure de base. Ensuite il est nécessaire, pour obtenir les ordres de mots corrects, d'effectuer des mouvements. Une langue SOV comme le japonais sera donc dérivée ainsi : SVO → S_VO → SO_V_.
L'un des avantages de la théorie est qu'elle permet de prédire correctement l'impossibilité de beaucoup de phénomènes. C'est le cas par exemple des langues V2 comme l'Allemand. Si on part du principe que le schéma X-barre peut contenir autant d'adjoint qu'il veut, comme c'était le cas pré-Kayne, comment expliquer l'asymétrie suivante :
-Peter tänzte Gestern
-Gestern tänzte Peter
-*Gestern Peter tänzte
La théorie X-barre ici ne pourrait pas expliquer pourquoi l'adverbe "Gestern" ne peut pas s'adjoindre au-dessus de Peter. La théorie antisymétrique postule en revanche que dans les langues V2, le verbe est obligé de monter en C°. Dès lors, CP ne pouvant prendre qu'un seul adjoint, soit le sujet "Peter" peut monter occuper la position la plus haute de l'arbre, à savoir le spécifieur de CP, soit l'adverbe peut monter occuper cette position. Mais il n'est pas possible d'avoir une seconde adjonction car ce phénomène est banni par la LCA.
Dérivés
[modifier | modifier le code]Le concept de la LCA a inspiré beaucoup de linguistes qui s'en sont servis pour dériver ses conséquences diverses. On pourra ainsi citer le développement de l'antisymétrie dynamique par Andrea Moro ou encore la dérivation d'une théorie antisymétrique des propositions relatives par Valentina Bianchi.
Références
[modifier | modifier le code]- (en) Richard S. Kayne, The Antisymmetry of Syntax. : Linguistic Inquiry Monograph Twenty-Five., The MIT Press: Cambridge., .
- (en) Cours de linguistique générale. : ., éd. Payot., .
- (en) Dryer Matthew et Martin Haspelmath(eds), The World Atlas of Language Structures Online. : ., Leipzig: Max Planck Institute for Evolutionary Anthropology., (lire en ligne)
