Feuilletage de Reeb
Cet article est une ébauche concernant la topologie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
En mathématiques, un feuilletage de Reeb est un type particulier de feuilletage de la sphère en trois dimensions, introduit par le mathématicien français Georges Reeb (1920–1992). Le principe est de diviser la sphère en deux tores solides tridimensionnels, dont le bord commun est un tore bidimensionnel (voir Tore de Clifford). Chacun des tores tridimensionnels est alors muni d'un feuilletage de codimension 1, et la surface torique intermédiaire constitue une feuille supplémentaire, qui est la seule feuille compacte du feuilletage.
D'après le théorème de la feuille compacte de Novikov, tout feuilletage continûment différentiable de la sphère tridimensionnelle comprend une feuille torique compacte.
-
Section bidimensionnelle d'un feuilletage de Reeb. -
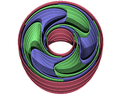
Modèle tridimensionnel d'un feuilletage de Reeb.
Annexes
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]- Georges Reeb, Sur certaines propriétés topologiques des variétés feuilletées, vol. 1183, Paris, Hermann, coll. « Actualités Sci. Indust. », .
- (en) Alberto Candel et Lawrence Conlon, Foliations, Providence (R.I.), American Mathematical Society, , 545 p. (ISBN 0-8218-0809-5, lire en ligne), p. 93.
- (en) Ieke Moerdijk et J. Mrčun, Introduction to Foliations and Lie Groupoids, vol. 91, Cambridge University Press, coll. « Cambridge studies in advanced mathematics », (ISBN 0-521-83197-0), p. 8.
Liens externes
[modifier | modifier le code]- (en) Eric W. Weisstein, « Reeb Foliation », sur MathWorld
