Équation du mouvement
L'équation du mouvement est une équation mathématique décrivant le mouvement d'un objet physique.
En général, l'équation du mouvement comprend l'accélération de l’objet en fonction de sa position, de sa vitesse, de sa masse et de toutes variables affectant l'une de celles-ci. Cette équation est surtout utilisée en mécanique classique et est normalement représentée sous la forme de coordonnées sphériques, coordonnées cylindriques ou coordonnées cartésiennes et respecte les lois du mouvement de Newton.
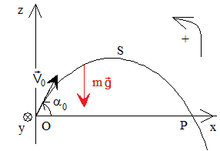
Équation du mouvement d'une particule dans l'espace dans un champ de pesanteur[modifier | modifier le code]
On considère une particule ponctuelle de masse m.
On prend pour hypothèses :
- référentiel galiléen
- les forces de frottement sont négligées
La force qui s'applique à cette particule au point est décrite par la relation : .
P = mg (g accélération de la pesanteur) correspond au poids. On trouve l'équation du mouvement à l'aide du principe fondamental de la dynamique (PFD).
avec , le vecteur accélération. Dans un système de coordonnées cartésiennes, le vecteur est orientée suivant .
On a donc trois équations :
Équations du mouvement dans l'espace d'une particule chargée dans un champ électromagnétique[modifier | modifier le code]
Soit une particule ponctuelle de masse et de charge soumise à un champ électrique et un champ magnétique .
On prend pour hypothèses :
- référentiel galiléen
- on néglige les forces de pesanteur et de frottement
La force qui s'applique à cette particule au point est décrite par la relation :
On trouve l'équation du mouvement à l'aide du principe fondamental de la dynamique (PFD).
avec , le vecteur accélération.
On trouve trois équations :
- Avec , et les coordonnées cartésiennes spatiales des champs , et .
























