Théorème de Holditch

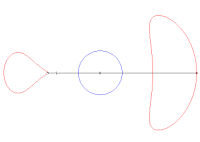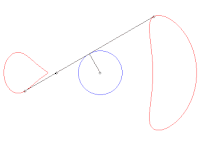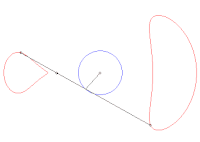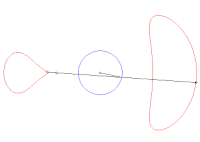
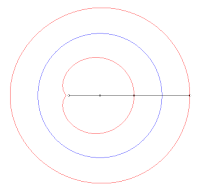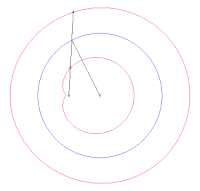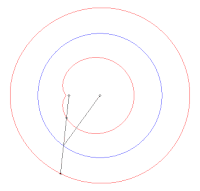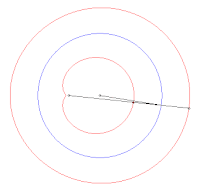
En géométrie plane, le théorème de Holditch affirme que si une corde de longueur fixe glisse le long d'une courbe fermée convexe, alors le domaine de Holditch délimité par la courbe de départ et le lieu géométrique tracé par un point de la corde situé à une distance $a$ d'une extrémité et $b$ de l'autre (la courbe de Holditch, supposée sans point double) a pour aire la valeur remarquable $\pi ab$ , indépendante à la fois de la forme et de la longueur de la courbe de départ.

En particulier, si le point traceur est situé en milieu de corde, l'aire du domaine de Holditch est égale à l'aire du disque de diamètre la corde.

Le théorème a été publié en 1858 ^[1] par le révérend Hamnet Holditch, président du Caius College, à Cambridge.

Pour Clifford Pickover, ce théorème fait partie des 250 évènements marquants de l'histoire des mathématiques^[2].

Illustrations[modifier | modifier le code]

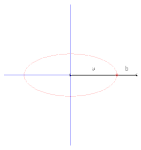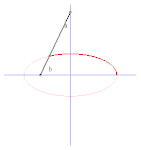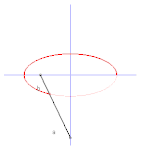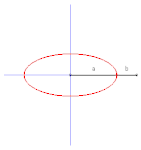
Illustration du théorème de Holditch dans le cas d'une courbe extérieure elliptique. On remarque que la courbe de Holditch n'est pas convexe.
La trajectoire d'un point de ce wagon est une courbe de Holditch associée à la courbe suivie par les rails.
Cas d'une courbe extérieure carrée. Cela permet de retrouver l'aire de l'ellipse.

Premières applications[modifier | modifier le code]

Aire d'une couronne[modifier | modifier le code]

L’aire d’une couronne circulaire dont on connait la longueur $\ell$ d’une corde tangente au cercle intérieur vaut $\pi \ell ^{2}/4$ , ceci quel que soit le rayon du cercle extérieur.

Aire de l'ellipse[modifier | modifier le code]

Si la courbe de départ est un carré de côté de longueur $a+b$ (voir l'illustration ci-dessus), d'après la construction de l'ellipse par la méthode de la bande de papier, la courbe de Holditch est formée de 4 quarts d'ellipses de demi-axes $a$ et $b$ . Le domaine de Holditch est donc formé de 4 quarts de domaines elliptiques ; par le théorème de Holditch, on retrouve bien la formule classique $\pi ab$ de l'aire de l'ellipse.

Généralisation de R. Estève[modifier | modifier le code]

Énoncé[modifier | modifier le code]

Une droite orientée se déplace dans le plan en revenant à son point de départ en ayant tourné $n$ fois sur elle-même ( $n$ algébrique, suivant le sens de rotation). Trois points fixes $A,B,C$ sur cette droite décrivent trois courbes fermées, supposées toujours simples, mais non forcément convexes, $C_{A}$ , $C_{B}$ , $C_{C}$ . On note $S_{A},S_{B},S_{C}$ les aires algébriques (positives en cas de parcours dans le sens trigonométrique, négatives sinon) des domaines délimités par les courbes $C_{A},C_{B},C_{C}$ . On a alors la relation de Holditch générale^[3]^,^[4] :

$S_{A}.{\overline {BC}}+S_{B}.{\overline {CA}}+S_{C}.{\overline {AB}}+n\pi .{\overline {AB}}.{\overline {BC}}.{\overline {CA}}=0$ .

Posant ${\overline {AC}}=a$ et ${\overline {CB}}=b$ , la relation s'écrit aussi $S_{C}={\frac {bS_{A}+aS_{B}}{a+b}}-n\pi ab$ .

On retrouve bien le théorème de Holditch dans le cas où les courbes $C_{A}$ et $C_{B}$ sont identiques et $n=1$ . La relation précédente s'écrit alors en effet $S_{C}=S_{A}-\pi ab$ , ce qui donne bien la relation de Holditch.

Démonstration[modifier | modifier le code]

Cette démonstration est tirée de ^[3].

On suppose ici les fonctions de classe $C^{1}$ par morceaux.

Un repère polaire $(O,{\overrightarrow {i}})$ étant choisi, désignons par $\theta =\theta (t)$ l'angle entre ${\overrightarrow {i}}$ et la droite orientée $(ABC)$ .

Posant ${\overline {AC}}=a$ , ${\overline {CB}}=b$ et $(x,y)$ les coordonnées de $C$ , les coordonnées de $A$ sont $(x_{1}=x-a\cos \theta ,y_{1}=y-a\sin \theta )$ , celles de $B$ sont $(x_{2}=x+b\cos \theta ,y_{2}=y+b\sin \theta )$ .

On obtient $x_{1}dy_{1}=(x-a\cos \theta )(dy-a\cos \theta d\theta ),x_{2}dy_{2}=(x+b\cos \theta )(dy+b\cos \theta d\theta )$ , d'où $bx_{1}dy_{1}+ax_{2}dy_{2}=(a+b)(xdy+ab\cos ^{2}\theta d\theta )$ .

Le mouvement s'effectuant entre $0$ et $T$ , on obtient $b\int _{0}^{T}x_{1}dy_{1}+a\int _{0}^{T}x_{2}dy_{2}=(a+b){\Biggl (}\int _{0}^{T}xdy+ab\int _{0}^{2n\pi }cos^{2}\theta d\theta {\Biggl )}$ , ce qui donne ${bS_{A}+aS_{B}}=(a+b)(S_{C}+n\pi ab)$ , soit $S_{C}={\frac {bS_{A}+aS_{B}}{a+b}}-n\pi ab$ .

Une élégante démonstration vectorielle se trouve dans ^[5].

Applications[modifier | modifier le code]

Aire de l'ellipse[modifier | modifier le code]

Construction de l'ellipse par la méthode de la bande de papier.

Lorsque les points $A$ et $B$ décrivent deux segments en croix, le point $C$ décrit l'ellipse de paramètres $a$ et $b$ (voir animation ci-dessus). L'ellipse est parcourue dans le sens trigonométrique donc l'aire $S_{C}$ est positive, mais le segment tourne dans l'autre sens, donc $n=-1$ . Les deux autres aires sont nulles, on retrouve $S_{C}=\pi ab$ .

Relation de Stewart[modifier | modifier le code]

On fait tourner la droite d'un tour autour d'un point $M$ du plan ; les courbes $C_{A},C_{B},C_{C}$ sont des cercles de centre $M$ , et la relation générale de Holditch divisée par $\pi$ donne celle de Stewart : ${MA}^{2}.{\overline {BC}}+{MB}^{2}.{\overline {CA}}+{MC}^{2}.{\overline {AB}}+{\overline {AB}}.{\overline {BC}}.{\overline {CA}}=0$ .

Théorème de Mamikon dans un cas particulier[modifier | modifier le code]

L'aire colorée vaut $\pi a^{2}$ où $a$ est la longueur du segment.

Énoncé[modifier | modifier le code]

L'aire balayée par un segment $[AC]$ de longueur constante $a$ restant tangent en $A$ à la courbe fermée simple décrite par $A$ vaut $\pi a^{2}$ .

Le théorème de Mamikon proprement dit s'occupe du cas plus général où le segment n'est plus forcément de longueur constante et où la courbe est quelconque.

Notons que Holditch utilise cette propriété, qu'il doit considérer comme évidente, dans sa démonstration ^[4]^,^[1].

Démonstration[modifier | modifier le code]

On part de la relation de Holditch $S_{A}.{\overline {BC}}+S_{B}.{\overline {CA}}+S_{C}.{\overline {AB}}+n\pi .{\overline {AB}}.{\overline {BC}}.{\overline {CA}}=0$ en posant ${\overline {AC}}=a$ et ${\overline {BC}}=b$ ; on obtient alors $S_{C}={\frac {aS_{B}-bS_{A}}{a-b}}+n\pi ab$ ; si on suppose que $B$ décrit la même courbe que $A$ et comme $n=1$ car on ne fait qu'un tour, on obtient $S_{C}=S_{A}+\pi ab$ . Si maintenant l'on fait tendre $b$ vers $a$ , alors $B$ tend vers $A$ en restant sur la courbe décrite par $A$ , et le segment $[AC]$ devient tangent à cette courbe ; on obtient $S_{C}-S_{A}=\pi a^{2}$ , ce que nous voulions.

Application à la tractrice[modifier | modifier le code]

La courbe décrite par le point $C$ est une courbe équitangentielle de celle décrite par $A$ . Lorsqu'on impose que cette dernière soit rectiligne, la courbe de départ est la tractrice. Pour obtenir une courbe "fermée" on ajoute la symétrique de la tractrice par rapport à son asymptote et l'aire ainsi formée vaut $\pi a^{2}$ d'après ce qui précède. L'aire entre la tractrice et son asymptote vaut donc $\pi a^{2}/2$ .

Aire d'une épitrochoïde ou d'une hypotrochoïde[modifier | modifier le code]

Un disque de rayon $R$ roule extérieurement, dans le sens trigonométrique, sur un disque de rayon $nR$ ; le segment $[AB]$ considéré ici est un segment lié au disque roulant centré sur le centre de ce disque et de longueur $2l$ , et on prend $a=b=l$ , de sorte que le point $C$ est le centre du disque mobile. Il est classique que le disque effectue alors $n+1$ tours autour du disque fixe pour revenir à son point de départ. De plus les points $A$ et $B$ décrivent deux épitrochoïdes identiques à rotation près, donc on peut poser $S_{A}=S_{B}=S$ .

La relation générale de Holditch s'écrit donc $\pi (n+1)^{2}R^{2}={\frac {2lS}{2l}}-(n+1)\pi l^{2}$ , ce qui donne $S=\pi (n+1)((n+1)R^{2}+l^{2})$ .

De la même façon pour une hypotrochoïde, on obtient : $S=\pi (n-1)((n-1)R^{2}+l^{2})$ .

Ces formules permettent d'obtenir l'aire de la cardioïde ou de l'astroïde par exemple.

Aire d'une arche de trochoïde[modifier | modifier le code]

Cette fois le disque roule sur une droite. Après avoir effectué un tour on le ramène au point de départ par mouvement rectiligne. Tous raisonnements faits, la relation de Holditch donne $0={\frac {lS-l(4\pi Rl-S)}{2l}}-\pi l^{2}$ où $S$ est l'aire d'une arche limitée par la base. On obtient $S=\pi l(2R+l)$ . Le cas $l=R$ donne l'aire $3\pi R^{2}$ de l'arche de cycloïde.

Aire de courbes associées au système bielle-manivelle[modifier | modifier le code]

Dans cet exemple, le point traceur est situé au quart de la bielle, donc l'aire délimitée par la courbe rouge vaut un quart de celle du disque.

Ici le point $A$ décrit un cercle de rayon $R$ et le point $B$ a un mouvement rectiligne. Le segment $[AB]$ n'effectue pas de tour sur lui-même, donc $n=0$ et l'aire $S_{B}$ est nulle. On obtient $S_{C}={\frac {b}{a+b}}\pi R^{2}$ ; il est remarquable que cette aire ne dépend que de la dimension du cercle et de la position du point traceur sur la bielle, pas de la longueur de celle-ci.

Voir à courbe de la bielle de Bérard.

Cas où la droite (ABC) passe par un point fixe O ; aires de conchoïdes[modifier | modifier le code]

D'une part, la relation de Holditch se démontre simplement à partir de celle de Stewart dans ce cas :

Démonstration

Un repère polaire $(O,{\overrightarrow {i}})$ étant choisi, posons $\theta (t)$ l'angle entre ${\overrightarrow {i}}$ et la droite orientée $(A(t)B(t)C(t))$ . En omettant les (t), posons $\rho _{A}=OA,\rho _{B}=OB,\rho _{C}=OC$ .

On part de la relation de Stewart : $\rho _{A}^{2}{\overline {BC}}+\rho _{B}^{2}{\overline {CA}}+\rho _{C}^{2}{\overline {AB}}+{\overline {AB}}.{\overline {BC}}.{\overline {CA}}=0$ .

Le mouvement ayant lieu sur $[0,T]$ , en multipliant par $\theta '(t)/2$ et intégrant entre $0$ et $T$ , on obtient ${{\overline {BC}} \over 2}\int _{0}^{T}{\rho _{A}^{2}\theta 'dt}+{{\overline {CA}} \over 2}\int _{0}^{T}{\rho _{B}^{2}\theta 'dt}+{{\overline {AB}} \over 2}\int _{0}^{T}{\rho _{C}^{2}\theta 'dt}+{\frac {{\overline {AB}}.{\overline {BC}}.{\overline {CA}}}{2}}\int _{0}^{T}{\theta 'dt}=0$ .

Comme $\int _{0}^{T}{{1 \over 2}{\rho _{A}^{2}\theta 'dt}}=S_{A},etc$ , et $\int _{0}^{T}{\theta 'dt}=\theta (T)-\theta (0)=2n\pi$ , on obtient bien $S_{A}.{\overline {BC}}+S_{B}.{\overline {CA}}+S_{C}.{\overline {AB}}+n\pi .{\overline {AB}}.{\overline {BC}}.{\overline {CA}}=0$ .

D'autre part, les trois courbes décrites par $A,B,C$ sont des conchoïdes de pôle $O$ les unes par rapport aux autres.

En particulier si ${\overline {AC}}={\overline {CB}}=a$ , Les courbes $C_{A}$ et $C_{B}$ sont des conchoïdes de $C_{C}$ de modules respectifs $-a$ et $a$ , et la relation de Holditch s'écrit : $S_{A}+S_{B}=2(S_{C}+n\pi a^{2})$ .

Dans les exemples ci-dessous, $C_{C}$ est un cercle de rayon $R$ .

L'aire de la grande conchoïde est égale à celle de la petite plus deux fois celle du disque.
La moyenne des aires des conchoïdes est égale à celle du disque plus $\pi a^{2}$ .
L'aire de la conchoïde est égale au double de celle du disque plus $\pi a^{2}$

Dans la première illustration ci-dessus où le pôle est à l'extérieur du cercle $C_{C}$ , $S_{B}-|S_{A}|=2\pi R^{2}$ car la droite n'effectue pas de tour sur elle-même et $C_{A}$ est parcouru en sens contraire du trigonométrique.

Dans la deuxième illustration où le pôle est à l'intérieur du cercle, $S_{B}+S_{A}=2\pi (R^{2}+a^{2})$ car la droite effectue un tour et $C_{A},C_{B}$ sont parcourues dans le sens trigonométrique.

Dans la troisième illustration, le pôle est sur le cercle, et les deux courbes $C_{A},C_{B}$ sont identiques, mais le cercle est parcouru deux fois quand la droite $(ABC)$ fait un tour. On obtient donc $S_{A}=S_{B}=2\pi R^{2}+\pi a^{2}$ . La conchoïde est dans ce cas un limaçon de Pascal.

Notes et références[modifier | modifier le code]

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Holditch's theorem » (voir la liste des auteurs).

↑ ^{a et b} (en) H. Holditch, « Geometrical theorem », The Quarterly Journal of Pure and Applied Mathematics,‎ 1858, p. 38 (lire en ligne)
↑ (en) Clifford Pickover, Le beau livre des maths, Paris, Dunod, 2010, p. 250
↑ ^{a et b} R. Estève, « Sur la formule d'Holditch et les applications qu'on peut en déduire », Nouvelles annales de mathématiques,‎ mai 1923 (lire en ligne)
↑ ^{a et b} (en) A. Broman, « "A fresh look at a long-forgotten theorem", », Mathematics Magazine 54(3),‎ mai 1981, p. 99–108 (lire en ligne)
↑ Arkadiusz Ploski, « Sur l'aire balayée par un segment mobile », 13 décembre 1996 (consulté le 21 novembre 2019)

Voir aussi[modifier | modifier le code]

Bibliographie[modifier | modifier le code]

B. Williamson, FRS, An elementary treatise on the integral calculus : 8ème édition 1906 pp. 206-211
M.A. Hacar Benitez, Numerosas aplicaciones de un teorema olvidado de geometria, Rev. Obras Publicas 127 (1980) 415–428.
W. Bender, The Holditch curve tracer, Mathematics Magazine, (mars 1981)
E. Kilic et S. Keles, On Holditch's Theorem and Polar Inertia Momentum, Commun. Fac. Sci. Univ. Ank. Ser. A, 43 (1994), 41-47.
M.J. Cooker, An Extension of Holditch's Theorem on the Area within a Closed Curve, Math. Gaz., 82 (1998), 183-188.
M.J. Cooker, On Sweeping out an Area, Math. Gaz., 83 (1999), 69–73.
J.P. Truc, le théorème de Holditch, Quadrature N°75, (2010), p. 10-18.
T.M. Apostol, M.A. Mnatsakanian, New Horizons in Geometry. ,Math. Assoc. Amer., Washington, DC, (2013), Section 9.13
J. Monterde, D. Rochera, Holditch's Ellipse Unveiled, the American Mathematical Monthly, Vol. 124, No. 5 (Mai 2017), pp. 403-421

Liens externes[modifier | modifier le code]

Portail de la géométrie

[:2-1] {a et b} (en) H. Holditch, « Geometrical theorem », The Quarterly Journal of Pure and Applied Mathematics,‎ 1858, p. 38 (lire en ligne)

[2] (en) Clifford Pickover, Le beau livre des maths, Paris, Dunod, 2010, p. 250

[:0-3] {a et b} R. Estève, « Sur la formule d'Holditch et les applications qu'on peut en déduire », Nouvelles annales de mathématiques,‎ mai 1923 (lire en ligne)

[:1-4] {a et b} (en) A. Broman, « "A fresh look at a long-forgotten theorem", », Mathematics Magazine 54(3),‎ mai 1981, p. 99–108 (lire en ligne)

[5] Arkadiusz Ploski, « Sur l'aire balayée par un segment mobile », 13 décembre 1996 (consulté le 21 novembre 2019)

[1]

[2]

[3]

[4]

[5]