Ondelette de Haar

Cet article est une ébauche concernant les mathématiques. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

L'ondelette de Haar

L'ondelette de Haar, ou fonction de Rademacher, est une ondelette créée par Alfréd Haar en 1909. On considère que c'est la première ondelette connue. Elle est la plus simple à comprendre et à implémenter. C'est une fonction dilatée et/ou translatée de la fonction mère ψ qui vaut :

$\psi(t)= \left\{ \begin{array}{l l} 1 & \quad \textrm{pour} \;\; 0\le t < \frac12\\ -1 & \quad \textrm{pour} \;\;\frac12\le t <1 \\ 0 & \quad \textrm{sinon}\\ \end{array} \right.$

Une généralisation est ce qu'on appelle le Système de Haar.

Le système de Haar

Le Système de Haar est une suite de fonctions continues par morceaux, appartenant à $L^p( [0,1])$ pour $1 \leq p < + \infty$ . Il est défini de la manière suivante :

• $h_1(t) = 1 \, \forall t \in [0,1]$

• Pour $k \geq 0$ et $1 \leq l \leq 2^k$ :

$h_{2^k+l}(t) = 1$ si $\frac{2l-2}{2^{k+1}} < t < \frac{2l-1}{2^{k+1}}$

$h_{2^k+l}(t) = -1$ si $\frac{2l-1}{2^{k+1}} < t < \frac{2l}{2^{k+1}}$

et $0$ ailleurs.

Voici les représentations graphiques de $h_2$ et de $h_3$ :

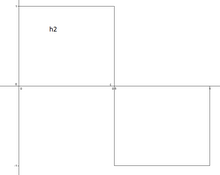
Une des propriétés intéressantes du système de Haar est qu'il est une Base de Schauder de $L^p( [0,1])$ pour $1 \leq p < + \infty$ .

Articles connexes

• Caractéristiques pseudo-Haar
• Base de Hilbert