Monoïde des traces

En mathématiques et en informatique, une trace est un ensemble de mots, où certaines lettres peuvent commuter, et d'autres non. Le monoïde des traces ou monoïde partiellement commutatif libre est le monoïde quotient du monoïde libre par une relation de commutation de lettres.

Le monoïde des traces est donc une structure qui se situe entre le monoïde libre et le monoïde commutatif libre. L'intérêt mathématique du monoïde des traces a été mis en évidence dans l'ouvrage fondateur Cartier et Foata 1969. Les traces apparaissent dans la modélisation en programmation concurrente, où les lettres qui peuvent commuter représentent des parties de processus qui peuvent s'exécuter de façon indépendante, alors que les lettres qui ne commutent pas représentent des verrous, leur synchronisation ou l'union de threads. Ce modèle a été proposé dans Mazurkiewicz 1977.

Définition[modifier | modifier le code]

Soit $A$ un alphabet. Une relation d'indépendance ou relation de commutation $I\subset A\times A$ est une relation binaire sur $A$ qui est irréflexive et symétrique. Le couple $(A,I)$ est le graphe d'indépendance ou graphe de commutation. Le complément $D=A\times A\setminus I$ d'une relation d'indépendance est une relation de dépendance. C'est une relation réflexive et symétrique. Le couple $(A,D)$ est le graphe de dépendance.

Exemple[modifier | modifier le code]

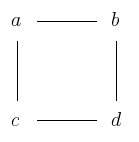
Soit $A=\{a,b,c,d\}$ et $I=\{(a,d),(d,a),(b,c),(c,b)\}$ . Le graphe d'indépendance et le graphe de dépendance, si l'on omet les boucles, sont décrits dans les figures ci-contre.

Traces[modifier | modifier le code]

La relation d'indépendance $I$ induit sur $A^{*}$ une relation d'équivalence notée $\sim$ . Deux mots $x$ et $y$ sont équivalents modulo $\sim$ s'il existe une suite $z_{1},\ldots ,z_{k}$ de mots tels que $x=z_{1}$ , $y=z_{k}$ , et pour $i=1,\ldots ,k-1$ , il existe des mots $u_{i},v_{i}$ et des lettres $a_{i},b_{i}$ tels que $z_{i}=u_{i}a_{i}b_{i}v_{i}$ et $z_{i+1}=u_{i}b_{i}a_{i}v_{i}$ et $(a_{i},b_{i})\in I$ . Ainsi, deux mots sont équivalents exactement quand ils peuvent être obtenus, l'un de l'autre, par une suite de transpositions de lettres indépendantes adjacentes. La relation $\sim$ est une congruence. Le quotient de $A^{*}$ par $\sim$ est donc un monoïde. C'est le monoïde partiellement commutatif libre induit par $I$ . Il est noté $M(A,I)$ . Les éléments de $M(A,I)$ , qui ont les classes d'équivalence de mots pour la relation $\sim$ , sont appelés des traces, et le monoïde $M(A,I)$ est appelé le monoïde des traces. Le morphisme de $A^{*}$ sur $M(A,I)$ qui associe à un mot $x$ sa trace, notée $[x]$ , est appelé le morphisme canonique.

Si la relation $I$ est vide, le monoïde $M(A,I)$ est le monoïde libre sur $A$ . Si $I=A\times A$ , alors $M(A,I)$ est le monoïde commutatif libre sur $A$ .

Exemple (suite)[modifier | modifier le code]

Pour la relation $I$ donnée dans l'exemple, on a

[baadcb]=\{baadcb,baadbc,badacb,bdaacb,bdaabc,badabc\}

Pour un mot $x$ de $A^{*}$ , on note ${\text{alph}}(x)$ l'ensemble des lettres qui apparaissent dans $x$ . Comme tous les mots de la trace $[x]$ ont le même alphabet, l'écriture ${\text{alph}}(t)$ , où $t$ est une trace, a un sens.

Une trace $t$ est connexe si toutes les lettres de ${\text{alph}}(t)$ appartiennent à la même composante connexe de $(A,D)$ . Deux traces $u$ et $v$ sont indépendantes si ${\text{alph}}(u)\times {\text{alph}}(v)\subset I$ .

Propriétés[modifier | modifier le code]

Lemme de projection[modifier | modifier le code]

On note $\pi _{a,b}$ le morphisme de projection de $M(A,I)$ dans lui-même qui efface toutes les lettres sauf $a$ et $b$ et laisse ces deux lettres inchangées.

Soient $u,v\in M(A,I)$ . On a $u=v$ si et seulement si $\pi _{a,b}(u)=\pi _{a,b}(v)$ pour tout $(a,b)\in D$ .

Simplifiabilité[modifier | modifier le code]

Le monoïde de traces $M(A,I)$ est un semi-groupe, c'est-à-dire que pour $u,x,y,v,\in M(A,I)$ , l'équation $uxv=uyv$ implique $x=y$ .

Lemme de Levi[modifier | modifier le code]

Le résultat suivant est l'analogue, pour les monoïdes de traces, du lemme de Levi des monoïdes libres.

Soient $x$ , $y$ , $x'$ , $y'$ des traces. Si $xy=x'y'$ , il existe des traces $p,r,p',r'$ , avec $r,r'$ indépendantes, telles que

x=pr,y=r'p',x'=pr',y'=rp'

.

Formes normales[modifier | modifier le code]

Il existe deux formes normales pour les éléments d'un monoïde partiellement commutatif libre, la forme normale lexicographique et la forme normale de Foata. La forme normale lexicographique est due à Anatolij V. Anisimov et Donald Knuth, la forme normale de Foata est due à Pierre Cartier et Dominique Foata qui ont étudié le monoïde des traces pour ses propriétés combinatoires.

L'alphabet $A$ est supposé totalement ordonné. On note $<$ l'ordre lexicographique induit sur $A^{*}$ . Un mot $x$ de $A^{*}$ est en forme normale lexicographique s'il est minimal, pour cet ordre, parmi les mots de la trace $[x]$ . Comme chaque trace est finie et que l'ordre lexicographique est un ordre total, toute trace a un unique représentant minimal qui est la forme normal lexicographique de la trace.

Un mot $x$ de $A^{*}$ est en forme normale de Foata si $x$ est le mot vide ou si $x=x_{1}\cdots x_{n}$ est le produit de $n>0$ mots non vides $x_{1},\ldots ,x_{n}$ tels que

chaque mot $x_{i}$ est composé de lettres qui commutent deux-à-deux, et $x_{i}$ est lexicographiquement minimal.

pour chaque $1\leq i<n$ et pour chaque lettre $a$ de $x_{i}$ , il existe une lettre $b$ de $x_{i+1}$ telle que $(a,b)\in D$ .

Exemple (suite)[modifier | modifier le code]

La forme normale lexicographique de $baadcb$ est $baadbc$ , et forme normale de Foata de $baadcb$ est $(b)(ad)(a)(bc)$ .

Langages de traces[modifier | modifier le code]

Un langage de traces est simplement un ensemble de traces. On peut considérer un tel ensemble comme l'image, par le morphisme canonique, d'un langage de mots.

Source[modifier | modifier le code]

Diekert et Métivier 1997

Références[modifier | modifier le code]

Ouvrages de référence[modifier | modifier le code]

(en) Volker Diekert et Yves Métivier, « Partial Commutation and Traces », dans G. Rozenberg, A. Salomaa (éditeurs), Handbook of Formal Languages, vol. 3 : Beyond Words, Springer Verlag, 1997 (ISBN 978-3-5406-0649-9, lire en ligne), p. 457-533
(en) Volker Diekert et Gregorz Rozenberg (éditeurs), The Book of Traces, Singapour, World Scientific, 1995, 576 p. (ISBN 978-981-02-2058-7, LCCN 94039387, lire en ligne)
(en) Antoni Mazurkiewicz, « Introduction to Trace Theory », dans V. Diekert, G. Rozenberg (éditeurs), The Book of Traces, World Scientific, 1995 (ISBN 9810220588), p. 3–41
(en) Volker Diekert, « Combinatorics on traces », Lecture Notes in Computer Science, vol. 454,‎ 1990, p. 9-29 (ISBN 3540530312)

Travaux historiques[modifier | modifier le code]

Pierre Cartier et Dominique Foata, Problèmes combinatoires de commutation et réarrangements, Springer-Verlag, coll. « Lecture Notes in Mathematics » (n^o 85), 1969, 576 p. (ISBN 978-981-02-2058-7, lire en ligne)
Version libre mise à jour, avec trois nouveaux appendices, à l'adresse http://www.emis.de/journals/SLC/books/cartfoa.html Commutation and Rearrangements An electronic reedition of the monograph
(en) Antoni Mazurkiewicz, Concurrent program schemes and their interpretations, DAIMI Report PB 78, Aarhus University, 1977

Voir aussi[modifier | modifier le code]

Langage formel