Ensemble d'arrivée
En mathématiques, pour une application ou une fonction[1] donnée f : A → B, l'ensemble B est appelé l'ensemble d'arrivée (on dit parfois le but de f ou le codomaine de f).
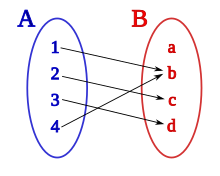
L'ensemble d'arrivée ne doit pas être confondu avec l'image f(A) de f, qui est en général seulement un sous-ensemble de B.
Exemple
[modifier | modifier le code]Soit la fonction f sur l'ensemble des nombres réels définie par
L'ensemble d'arrivée de f est mais f(x) ne prend jamais de valeurs négatives. L'image est en fait l'intervalle des réels positifs.
- .
Nous aurions pu définir une fonction g ainsi :
Tandis que f et g ont le même effet quand elles sont appliquées à un nombre réel donné, les fonctions sont différentes puisqu'elles ont des ensembles d'arrivée différents.
Surjectivité
[modifier | modifier le code]L'ensemble d'arrivée peut avoir un effet sur la surjectivité d'une fonction ; dans notre exemple, g est surjective alors que f ne l'est pas.
De manière générale, une application f : A → B est surjective si, et seulement si, son image est égale à son ensemble d'arrivée, c'est-à-dire .
À noter qu'on peut toujours, à partir d'une application construire une application surjective en restreignant son ensemble d'arrivée à l'image de : l'application définie par pour tout dans est surjective.
Voir aussi
[modifier | modifier le code]Article connexe
[modifier | modifier le code]Notes
[modifier | modifier le code]- Selon les sources, il y a distinction ou non entre les notions de fonction et d'application, voir Application_(mathématiques)#Fonction_et_application pour plus de détails. Ce qui est énoncé dans cet article est valable que la distinction soit faite ou non.












