Équation réduite
Apparence
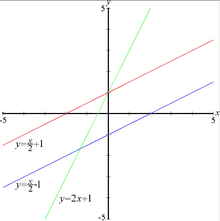
y = 2x + 1; y = ½x + 1; y = ½x − 1
L'équation réduite d'une droite du plan affine est une équation de droite de la forme y = ax + b (ou y = mx + p dans l’enseignement français). Le nombre a est appelé coefficient directeur, et b ordonnée à l'origine de la droite.
Toute droite non parallèle à l'axe des ordonnées d'un repère admet une unique équation réduite dans ce repère. Réciproquement, étant donnés un repère du plan et deux nombres réels a et b, l'ensemble des points de coordonnées (x ; y) tels que y = ax + b est une droite.
Une telle équation correspond à la représentation graphique de la fonction affine qui, à tout réel x, associe ax + b. Les techniques d'étude des fonctions peuvent être utilisées pour étudier la droite, et réciproquement.
