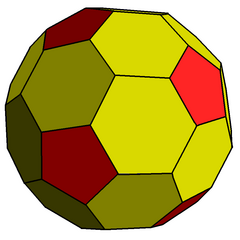
Triacontaèdre rhombique tronqué
| Triacontaèdre rhombique tronqué | |
|---|---|
| |
| Type | Quasi-solide de Johnson |
| Faces | 12 pentagones 30 hexagones |
| Arêtes | 120 (2 types) |
| Sommets | 80 (2 types) |
| Configurations de sommet | (60) 5.6.6 (20) 6.6.6 |
| Groupe de symétrie | Symétries de l'icosaèdre (Ih) |
| Polyèdre dual | Pentaki-icosidodécaèdre (en) |
| Propriétés | Convexe, faces équilatérales (mais non régulières) |
Le triacontaèdre rhombique tronqué est un polyèdre convexe obtenu par troncature des 12 sommets du triacontaèdre rhombique où 5 faces se rejoignaient.
Les 30 faces rhombiques (losanges) deviennent des hexagones non réguliers, et les 12 sommets tronqués deviennent des pentagones réguliers.
Les faces hexagonales peuvent être équilatérales, mais non régulières par une symétrie D2. Pour chaque face hexagonale, les angles aux deux sommets de configuration 6.6.6 valent , et aux quatre sommets restants de configuration 5.6.6 valent 121,717° chacun.

Ambiguïtés[modifier | modifier le code]
Il ne faut pas le confondre avec l'icosaèdre tronqué qui lui ressemble beaucoup, mais qui n'a que 20 hexagones :
-
Triacontaèdre rhombique tronqué
-
Icosaèdre tronqué
Ce n'est pas un solide de Johnson malgré les apparences, car bien que convexe, toutes ses faces ne sont pas strictement régulières, c'est également le cas du triakitétraèdre tronqué et du dodécaèdre rhombique tronqué.
Ce nom de « triacontaèdre rhombique tronqué » est ambigu, car seulement 12 des sommets originels ont été tronqués, alors qu'un polyèdre tronqué désigne généralement un polyèdre dont tous les sommets ont été tronqués. Un autre polyèdre complètement différent peut être obtenu par troncature de tous les sommets.
Chimie[modifier | modifier le code]
C'est la forme de la molécule de fullerène C80. Cette forme est parfois appelée C80(Ih), pour décrire sa symétrie de type icosaèdre le distinguer ainsi des autres fullerènes à 80 sommets, possédant moins de symétries.
Aire et volume[modifier | modifier le code]
Si son arête a pour longueur a,
- son volume vaut, en utilisant la formule du volume du triacontaèdre rhombique (où est le nombre d'or) :
- ;
- son aire vaut (où ) :
- .







