Symétrie circulaire
|

| |
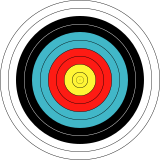
En 2 dimensions, une cible de tir à l'arc a une symétrie circulaire.
|
Une surface de révolution a une symétrie circulaire autour d'un axe en 3 dimensions.
|
En géométrie, la symétrie circulaire est un type de symétrie continue pour un objet plan qui peut pivoter selon n'importe quel angle arbitraire et établir une correspondance avec lui-même.
La symétrie circulaire de rotation est isomorphe au groupe circulaire dans le plan complexe, ou le groupe orthogonal spécial SO(2), et le groupe unitaire U(1). La symétrie circulaire de réflexion est isomorphe au groupe orthogonal O(2).
Deux dimensions
[modifier | modifier le code]Un objet bidimensionnel à symétrie circulaire est constitué de cercles concentriques et de domaines annulaires.
La symétrie circulaire de rotation possède toute la symétrie cyclique, Z n comme symétries de sous-groupes. La symétrie circulaire de réflexion a toute la symétrie dièdre, Dih n comme symétries de sous-groupes.
Trois dimensions
[modifier | modifier le code]
En 3 dimensions, une surface ou solide de révolution présente une symétrie circulaire autour d'un axe, également appelée symétrie cylindrique ou symétrie axiale. Un exemple est un cône de révolution (ou cône circulaire droit). La symétrie circulaire en 3 dimensions possède toute la symétrie pyramidale, C n v comme sous-groupes.
Un double-cône, un bicône, un cylindre, un tore et un sphéroïde ont une symétrie circulaire autour d'un axe, et ont en plus une symétrie bilatérale perpendiculaire à l'axe du système (ou symétrie demi-cylindrique ). Ces symétries circulaires de réflexion possèdent toutes les symétries prismatiques discrètes, D n h comme sous-groupes.
Quatre dimensions
[modifier | modifier le code]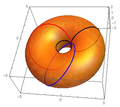 (simple) (simple)
|
 1:5 1:5
|
 5:1 5:1
|
| Cylindrique | Duocylindrique | |
|---|---|---|
En quatre dimensions, un objet peut avoir une symétrie circulaire, sur deux plans d'axes orthogonaux, ou une symétrie duocylindrique. Par exemple, le duocylindre et le tore de Clifford ont chacun une symétrie circulaire selon deux axes orthogonaux. Un sphérindre a une symétrie sphérique dans un espace à 3 dimensions et une symétrie circulaire dans la direction orthogonale.
Symétrie sphérique
[modifier | modifier le code]
Une symétrie en 3 dimensions analogue est la symétrie sphérique.
La symétrie sphérique de rotation est isomorphe au groupe de rotation SO(3) et peut être paramétrée par les rotations successives de Davenport, tangage, lacet et roulis. La symétrie sphérique de rotation possède tous les groupes de points chiraux 3D discrets comme sous-groupes. La symétrie sphérique de réflexion est isomorphe au groupe orthogonal O(3) et possède les groupes de points discrets tridimensionnels comme sous-groupes.
Un champ scalaire a une symétrie sphérique s'il ne dépend que de la distance à l'origine, comme le potentiel d'une force centrale. Un champ vectoriel a une symétrie sphérique s'il est radial dirigé vers l'intérieur ou l'extérieur avec une amplitude et une orientation (intérieur/extérieur) en fonction uniquement de la distance à l'origine, comme une force centrale.
Voir également
[modifier | modifier le code]Notes et références
[modifier | modifier le code]- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Circular symetry » (voir la liste des auteurs).
- (en) « Symétrie circulaire », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, (ISBN 978-1556080104, lire en ligne)
