Géographie généralisée

Un article de Wikipédia, l'encyclopédie libre.
Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus.
Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus.

Cet article ne cite pas suffisamment ses sources ().

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

En théorie de la complexité, géographie généralisé est un problème PSPACE-complet classique. Il est plus connu sous son nom anglais Generalized Geography et est abrégé GG.

Introduction[modifier | modifier le code]

À l'origine, Géographie est un jeu particulièrement adapté aux longs trajets en voiture dans lequel deux joueurs énoncent à tour de rôle différents noms de villes. Chaque nom de ville donné doit commencer par la dernière lettre du précédant (à l'exception du premier qui est librement choisi) et il est interdit de donner un nom de ville qui a déjà été employé. Le premier joueur qui ne peut pas donner de nom de ville respectant les contraintes perd la partie et le jeu prend alors fin.

Modélisation par graphe[modifier | modifier le code]

Le jeu peut être représenté par un graphe orienté dont les nœuds représentent les noms de ville du monde. Une flèche lie le nœud N1 au nœud N2 si et seulement si le nom de ville représenté par le nœud N2 commence par la dernière lettre de celui représenté par le nœud N1. Autrement dit, une flèche représente le fait qu'il est possible de passer d'une ville à une autre en accord avec les règles du jeu. Une partie correspond alors à une marche sur le graphe où les joueurs choisissent chacun leur tour un nœud voisin du nœud actuel qui n'a pas été visité. Le premier joueur qui en est incapable perd la partie. Un exemple illustré avec des noms de villes de l'État du Michigan (États-Unis) est présenté ci-dessous.

Dans le problème Géographie généralisée on considère simplement un graphe orienté dont l'un des sommets est spécifié être le sommet de départ (on ne choisit plus la première ville librement). Le graphe suivant illustre un exemple d'instance du problème GG.

Jouer une partie[modifier | modifier le code]

On définit P1 le joueur qui joue en premier et P2 le deuxième. On définit de plus N1, … , Nn les nœuds du graphe avec N1 le point d'entrée. Une partie jouée correspond à un chemin maximal ne passant jamais deux fois par le même sommet en commençant au nœud N1.

Complexité calculatoire[modifier | modifier le code]

Le problème GG qui consiste étant donné un graphe G et un sommet N1 à trouver quel joueur (P1 ou P2) a une stratégie gagnante est PSPACE-complet.

Géographie Généralisé est PSPACE-complet[modifier | modifier le code]

GG est PSPACE-complet. Cela signifie qu'il est à la fois PSPACE et PSPACE dur. On prouve ces deux affirmations séparément.

Géographie Généralisé est dans PSPACE.

Démonstration

Soit GG = { <G, b> | P1 a une stratégie gagnante sur le graphe g en commencant sur le sommet b dans une partie du jeu de géographie généralisé. }. On montre que GG est dans PSPACE en introduisant l'algorithme suivant, d'exécution polynomiale.

Entrée : <G, nstart>

  1. Mesurer l'arité de sortie de nstart. Si cette arité est 0 renvoyer « perdu ».
  2. Construire une liste des nœuds accessibles depuis nstart: L = n1, n2, … , ni.
  3. Construire G2 en extrayant nstart et toutes les arêtes qui lui sont reliées de G.
  4. Effectuer un appel récursif de paramètre <G2, n> pour chaque n dans L. Ces appels récursifs sont effectués séquentiellement. On ne paye donc que le cout mémoire de l'appel le plus couteux pour l'ensemble des appels récursifs.
  5. Si tous ces appels récursifs renvoient « gagné » renvoyer « perdu » (quoi que fasse P1 son adversaire peut gagner). Sinon renvoyer « gagné ».

L'algorithme décide clairement GG. On a de plus une profondeur de récursion maximale de n et le cout mémoire de chaque étape de récursion est linéaire en la taille de l'entrée. La mémoire consommée est donc bien polynomiale en la taille de l'entrée. GG est dans PSPACE.

Géographie généralisé est PSPACE-dur.

Démonstration

La preuve suivante est due à David Liechtenstein et Michael Sipser[1].

Nous allons établir que GG est PSPACE dur en réduisant FORMULA-GAME à GG en temps polynomial (on sait que FORMULA-GAME est lui-même PSPACE dur).

Une instance de FORMULA-GAME consiste en une formule booléenne quantifiée (close) φ = ∃x1 ∀x2 ∃x3 …Qxk(ψ) où Q est soit ∃ soit ∀ (avec alternance entre les quantificateurs ∃ et ∀). Deux joueurs PE et PA s'affrontent en choisissant successivement les valeurs des variables dans l'ordre de leur quantification. PE choisit la valeur des variables quantifiées par un ∃ et PA choisit les autres. On suppose que ψ est en forme normale conjonctive à clauses de taille 3. PE gagne si et seulement si la formule est vrai après toutes les quantifications.

Soit ψ une instance de FORMULA-GAME.

Sans perte de généralité, on suppose que le premier et le dernier quantificateurs sont des ∃. On peut toujours se ramener à ce cas en rajoutant des variables inutiles n'apparaissant pas dans ψ.

On réduit notre instance de FORMULA-GAME à une instance de GG selon le principe illustré par le schéma ci-dessus.

La stratégie optimale de P1 correspondra à celle de PE, et celle de P2 à celle de PA.

La chaîne verticale de gauche correspond au processus de choix des valeurs des variables. Le choix du chemin de gauche ou de droite dans chaque mini-tructure en diamant correspond au choix de la valeur d'une variable. Étant donné que le premier quantificateur est un ∃, PE joue en premier. Il faut que PE joue au début des diamants correspondant à des quantifications ∃ et PA au début des autres. Étant donné que le dernier quantificateur est universel, c'est au tour de P1 de jouer quand on sort du dernier diamant (il correspond à PE). P1 amène le jeu en c puis c'est à P2 de jouer.

On rappel qu'a ce stade dans FORMULA-GAME PE gagne si la formule est vraie et PA gagne si elle est fausse.

Si la formule est fausse (avec la valuation correspondant aux choix de chemins qui ont été faits), il suffit à P2 de choisir un chemin menant à une clause non satisfaite. P1 ne pourra alors que choisir un chemin menant à un littéral valué « faux », et laissera donc un dernier coup à P2 qui gagne la partie. Donc si PA gagne dans l'instance de FORMULA-GAME, P2 gagne dans notre instance de GG.

De même, si la formule est vrai alors quoi que choisisse P2 il a amené P1 dans une clause « vraie ». Ce dernier peut donc choisir un chemin menant à un littéral valué à vrai et gagne la partie.

Donc si PE gagne dans l'instance de FORMULA-GAME, P1 gagne dans notre instance de GG.

On a bien réduit l'instance donnée de FORMULA-GAME à une instance de GG par un procédé polynomial.

Donc GG est PSPACE dur.

Planar GG[modifier | modifier le code]

Le problème GG restreint aux graphes planaires (Planar GG) est toujours PSPACE-complet. La preuve suivant est issue du théorème 3 de [2].

Démonstration

Étant donné que GG est PSPACE et que planar GG est obtenu par une restriction des instances de GG, planar GG est dans PSPACE. Il nous reste à prouver que Planar GG est PSPACE dur. On prouve cela en reduisant FORMULA-GAME à Planar GG en passant par GG.

Partant d'une instance de FORMULA-GAME que nous avons déjà réduite à une instance de GG, on dessine le graphe de sorte que trois arêtes ne se croisent jamais en un point et que deux arêtes qui se croisent ne soient jamais utilisées dans la même partie. Cela n'est pas possible en général mais le devient dans le cas des graphes obtenus par la réduction de FORMULA-GAME à GG que nous avons décrit précédemment. Nous remplacons ensuite chaque croisement par la construction présentée dans le schéma ci-dessous.

The intersection is eliminated by adding 6 vertices and redrawing the edges as shown.

Le résultat est bien un graphe planaire. Une simple étude des cas possible montre qu'il n'est pas possible de « tourner » lorsqu'on emprunte cette structure de croisement sans perdre en très peu de coups. De plus, c'est bien au bon joueur de jouer quand on quitte cette structure.

Une partie jouée parfaitement sur le nouveau graphe ainsi obtenu aura donc le même résultat que sur le graphe obtenu en sortie de réduction depuis FORMULA-GAME.

Cette réduction est évidemment polynomiale. Planar GG est donc PSPACE complet.

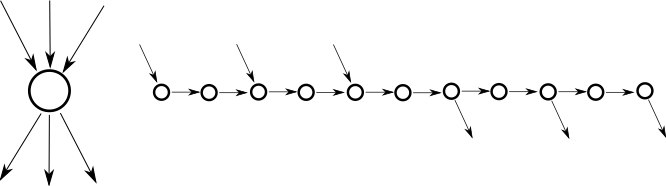
Graphes planaires bipartis d'arité maximale 3[modifier | modifier le code]

Le problème restreint aux graphes planaires bipartis d'arité maximale 3 est toujours PSPACE-dur. On le prouve en remplaçant les sommets d'arité strictement supérieure à trois par des chaines de sommets[1].

Edge Geography[modifier | modifier le code]

Il existe une variante de GG nommée Edge Geography (traduisible par « Géographie arête ») où, après chaque coup, on efface l’arête qui vient d'être employée mais où on peut passer plusieurs fois par le même nœud. Cela contraste avec GG, qui peut être vu comme effaçant les sommets empruntés à chaque étape. On peut donc considérer que GG est « Géographie sommet » (Vertex Geography).

Edge Geography est également PSPACE-complet. Cela se prouve en réduisant des formules booléennes quantifiées à des instances de Edge Geography [2].

Graphe non orienté[modifier | modifier le code]

On peut envisager une variante de GG basée sur des graphes non orientés. Fraenkel, Scheinerman, et Ullman[3] ont montré qu'Edge Geography non orienté est dans P tandis que GG non orienté est PSPACE-complet, même en se restreignant aux graphes plan d'arité maximale 3. Si on se restreint aux graphes bipartis, le problème peut être résolu en temps polynomial.

Notes et références[modifier | modifier le code]

  1. ↑ a et b David Lichtenstein et Michael Sipser, « Go Is Polynomial-Space Hard », Journal of the ACM, vol. 27, no 2,‎ , p. 393–401 (DOI 10.1145/322186.322201, lire en ligne)
  2. ↑ a et b Thomas J. Schaefer, « On the complexity of some two-person perfect-information games », Journal of Computer and System Sciences, vol. 16, no 2,‎ , p. 185–225 (DOI 10.1016/0022-0000(78)90045-4)
  3. ↑ Aviezri Fraenkel, Edward Scheinerman et Daniel Ullman, « Undirected edge geography », Theoretical Computer Science, vol. 112, no 2,‎ , p. 371–381 (DOI 10.1016/0304-3975(93)90026-p)

Bibliographie[modifier | modifier le code]

Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Géographie_généralisée&oldid=201138070 ».