Attaque boomerang
L'attaque boomerang est une version améliorée de la cryptanalyse différentielle, cette méthode a été inventée par David Wagner en 1999. Elle consiste à attaquer les deux moitiés d'un algorithme de chiffrement par bloc et part du principe que certaines propriétés, après perturbations des entrées, ne se propagent pas à travers toute la structure.
Description[modifier | modifier le code]
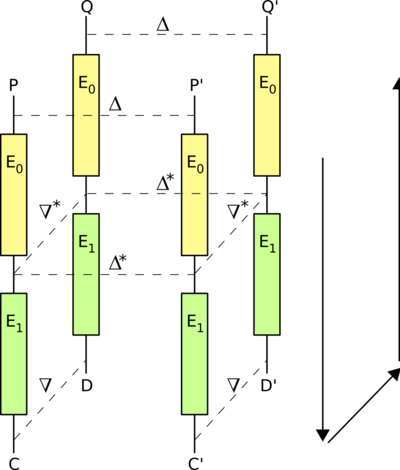
On considère quatre messages en clair : P, P', Q et Q'. On dispose également des versions chiffrées de ces messages : C, C', D et D'. On considère également un algorithme de chiffrement symétrique E dont le chiffrement peut être décomposé en deux parties : E0 et E1.
La première moitié du chiffrement est représentée par E0 et E1 est la deuxième partie. On définit deux caractéristiques différentielles Δ → Δ* pour E0 et ∇ → ∇* pour E1-1. Cette notation signifie qu'une modification Δ sur les entrées va entraîner une modification Δ* sur les sorties après passage dans l'algorithme. Le but est d'obtenir des caractéristiques qui vont satisfaire les données que nous avons.
On veut en premier que la paire (P, P') soit compatible avec la caractéristique de E0. Ensuite, les paires (P, Q) ainsi que (P', Q') doivent satisfaire la caractéristique de E1-1. Nous supposons ensuite que la paire (Q, Q') est configurée de telle manière que la caractéristique différentielle Δ* → Δ soit respectée.
Si les paramètres sont corrects, la différence entre Q et Q' doit être égale à la différence entre P et P' d'où le surnom de Boomerang.
Les différentes étapes[modifier | modifier le code]
Nous avons donc un bloc P et un bloc P' avec une différence Δ entre les deux. La différence se traduit sous la forme d'un ou-exclusif du bloc P avec un vecteur, on obtient alors P'. On calcule E0(P) et E0(P'). Ces deux résultats diffèrent de Δ*. On applique ensuite E1 sur ces deux valeurs pour obtenir C et C' :
- C = E1(E0(P))
- C' = E1(E0(P')).
On génère ensuite D et D' à partir de C et C' grâce à un ou-exclusif avec ∇ :
- D = C ∇
- D' = C' ∇
On déchiffre D et D' avec l'inverse de E1. On se trouve alors dans une couche intermédiaire avec deux résultats qui varient de Δ* si les caractéristiques des différences sont correctes. En déchiffrant avec E0, on trouve Q et Q'. Ceux-ci doivent présenter une différence de Δ, la même qu'entre P et P'. La différence initialement imposée sur P et P' est revenue entre Q et Q' comme un boomerang.
Grâce à cette approche, il est possible d'approcher successivement la clé en regardant si les conditions décrites ci-dessus sont respectées avec un grand nombre de paires claires/chiffrées.
Applications[modifier | modifier le code]
L'attaque Boomerang fonctionne efficacement sur plusieurs chiffrements. Dans son papier, David Wagner montre comment l'utiliser dans le cadre de Coconut98, une version simplifiée de Khufu de Ralph Merkle, 6 rondes de FEAL et de 16 rondes de CAST-256. En 2004, elle a été mise en pratique sur 6 rondes d'AES par Alex Biryukov.
Liens externes[modifier | modifier le code]
- (en) [ps] Papier original de David Wagner
- (en) Explication détaillée de l'attaque Boomerang
- (en) [PDF] Boomerang attack on 5 and 6 round-AES

