Graphe de Doyle
| Graphe de Doyle | |
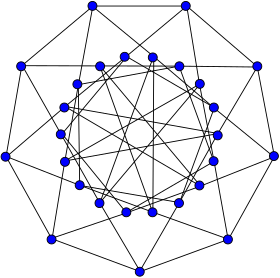 Représentation du graphe de Doyle | |
| Nombre de sommets | 27 |
|---|---|
| Nombre d'arêtes | 54 |
| Distribution des degrés | 4-régulier |
| Rayon | 3 |
| Diamètre | 3 |
| Maille | 5 |
| Automorphismes | 54 |
| Nombre chromatique | 3 |
| Indice chromatique | 5 |
| Propriétés | Régulier Eulérien Hamiltonien Cayley Sommet-transitif Arête-transitif |
| modifier |
|
Le graphe de Doyle (ou graphe de Holt) est, en théorie des graphes, un graphe 4-régulier possédant 27 sommets et 54 arêtes. C'est le plus petit graphe exemple de graphe étant sommet-transitif et arête-transitif mais pas symétrique[1],[2]. De tels graphes sont rares[3]. Il doit son nom à Peter G. Doyle et Derek F. Holt qui le découvrirent tous deux de façon indépendante en 1976[4] et 1981[5] respectivement.
Propriétés
[modifier | modifier le code]Propriétés générales
[modifier | modifier le code]Le diamètre du graphe de Doyle, l'excentricité maximale de ses sommets, est 3, son rayon, l'excentricité minimale de ses sommets, est 3 et sa maille, la longueur de son plus court cycle, est 5. Il s'agit d'un graphe 4-sommet-connexe et d'un graphe 4-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 4 sommets ou de 4 arêtes.
C'est également un graphe hamiltonien avec 98 472 cycles hamiltoniens distincts.
Coloration
[modifier | modifier le code]Le nombre chromatique du graphe de Doyle est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 2-coloration valide du graphe.
L'indice chromatique du graphe de Doyle est 5. Il existe donc une 5-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Propriétés algébriques
[modifier | modifier le code]Le groupe d'automorphismes du graphe de Doyle est un groupe d'ordre 54.
Le polynôme caractéristique de la matrice d'adjacence du graphe de Doyle est : .
Voir aussi
[modifier | modifier le code]Liens internes
[modifier | modifier le code]Liens externes
[modifier | modifier le code]- (en) Eric W. Weisstein, Doyle Graph (MathWorld)
Références
[modifier | modifier le code]- Doyle, P. "A 27-Vertex Graph That Is Vertex-Transitive and Edge-Transitive But Not L-Transitive." October 1998. [1]
- (en) Brian Alspach, Dragan Marušič et Lewis Nowitz, « Constructing Graphs which are ½-Transitive », Journal of the Australian Mathematical Society (Series A), vol. 56, no 3, , p. 391–402 (DOI 10.1017/S1446788700035564, lire en ligne).
- Jonathan L. Gross, Jay Yellen, Handbook of Graph Theory, CRC Press, 2004, (ISBN 1-58488-090-2), p. 491.
- P. G. Doyle On Transitive Graphs, Senior Thesis, 1976, Harvard College.
- (en) Derek F. Holt, « A graph which is edge transitive but not arc transitive », Journal of Graph Theory, vol. 5, no 2, , p. 201–204 (DOI 10.1002/jgt.3190050210).

