Équation de Sellmeier
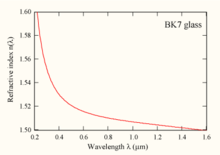
En optique, l’équation de Sellmeier est une relation empirique entre l'indice de réfraction et la longueur d'onde pour un milieu transparent donné. Cette équation est utilisée pour déterminer la dispersion de la lumière dans un milieu réfringent.
Cette équation a été trouvée en 1871 par Wilhelm Sellmeier, et était un développement du travail de Augustin Louis Cauchy sur la loi de Cauchy pour modéliser la dispersion[1].
Équation[modifier | modifier le code]
La forme habituelle de cette équation est[2] :
- ,
où B1,2,3 et C1,2,3 sont les coefficients de Sellmeier, propres à un matériau et déterminés expérimentalement. Ces coefficients sont généralement déterminés pour λ mesuré en micromètres (µm). λ est la longueur d'onde dans le vide et non pas celle dans le milieu d'intérêt, qui est .
Une forme différente de l'équation est parfois utilisée pour certains types de matériaux, par exemple les cristaux[réf. nécessaire]. Les coefficients de Sellmeier pour les verres optiques sont indiqués généralement dans les spécifications du verre lui-même.
Origine[modifier | modifier le code]
L'équation de Sellmeier résulte d'une approximation dans laquelle on considère que les particules du milieu réagissent au champ électromagnétique incident à la manière d'oscillateurs harmoniques. Dans le cadre de cette modélisation, on aboutit à la formule : ,
où M représente le nombre de pics de résonance pour les oscillateurs harmoniques aux longueurs d'onde λj, Bj des constantes obtenues empiriquement en adaptant le modèle aux mesures[3].
Coefficients[modifier | modifier le code]
| Matériau | B1 | B2 | B3 | C1 | C2 | C3 |
|---|---|---|---|---|---|---|
| Al2O3 Alumine (indice ordinaire) |
1,431 349 30 | 6,505 471 3 × 10−1 | 5,341 402 1 | 5,279 926 1 × 10−3 µm2 | 1,423 826 47 × 10−2 µm2 | 3,250 178 34 × 102 µm2 |
| Al2O3 Alumine (indice extraordinaire) |
1,503 975 9 | 5,506 914 1 × 10−1 | 6,593 737 9 | 5,480 411 29 × 10−3 µm2 | 1,479 942 81 × 10−2 µm2 | 4,028 951 4 × 102 µm2 |
| BK7 | 1,039 612 12 | 2,317 923 44 × 10−1 | 1,010 469 45 | 6,000 698 67 × 10−3 µm2 | 2,001 791 44 × 10−2 µm2 | 1,035 606 53 × 102 µm2 |
Notes et références[modifier | modifier le code]
- (de) Wilhelm Sellmeier, « Zur Erklärung der abnormen Farbenfolge im Spectrum einiger Substanzen », Annalen der Physik und Chemie, no 219, , p. 272-282
- (en) Refractive index and dispersion, Schott AG, coll. « Technical information » (no 29) (lire en ligne)
- (en) Alexis Mendez et T. F. Morse, Specialty optical fibers handbook, , 840 p. (lire en ligne), p. 39





