Utilisateur:MajSup/Brouillin ABR

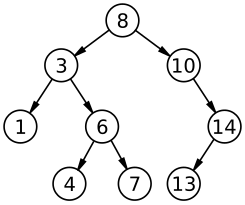
En informatique, un arbre binaire de recherche (ABR) est une structure de données pour représenter un ensemble ou un tableau associatif dont les clés appartiennent à un ensemble totalement ordonné. Un arbre binaire de recherche permet des opérations rapides pour rechercher une clé, insérer ou supprimer une clé.

Un arbre binaire de recherche est un arbre binaire dans lequel chaque nœud possède une clé, telle que chaque nœud du sous-arbre gauche ait une clé inférieure ou égale à celle du nœud considéré, et que chaque nœud du sous-arbre droit possède une clé supérieure ou égale à celle-ci — selon la mise en œuvre de l'ABR, on pourra interdire ou non des clés de valeur égale. Les nœuds que l'on ajoute deviennent des feuilles de l'arbre.

Opérations[modifier | modifier le code]

Recherche[modifier | modifier le code]

La rotation est une opération permettant d'équilibrer les arbres.

La recherche dans un arbre binaire d'un nœud ayant une clé particulière est un procédé récursif. On commence par examiner la racine. Si sa clé est la clé recherchée, l'algorithme se termine et renvoie la racine. Si elle est strictement inférieure, alors elle est dans le sous-arbre gauche, sur lequel on effectue alors récursivement la recherche. De même si la clé recherchée est strictement supérieure à la clé de la racine, la recherche continue dans le sous-arbre droit. Si on atteint une feuille dont la clé n'est pas celle recherchée, on sait alors que la clé recherchée n'appartient à aucun nœud, elle ne figure donc pas dans l'arbre de recherche. On peut comparer l'exploration d'un arbre binaire de recherche avec la recherche par dichotomie qui procède à peu près de la même manière sauf qu'elle accède directement à chaque élément d'un tableau au lieu de suivre des liens. La différence entre les deux algorithmes est que, dans la recherche dichotomique, on suppose avoir un critère de découpage de l'espace en deux parties que l'on n'a pas dans la recherche dans un arbre.

Cette opération requiert un temps en O(log(n)) dans le cas moyen, mais O(n) dans le cas critique où l'arbre est complètement déséquilibré et ressemble à une liste chaînée. Ce problème est écarté si l'arbre est équilibré par rotation au fur et à mesure des insertions pouvant créer des listes trop longues.

Pseudo code recherche élément

Insertion[modifier | modifier le code]

L'insertion d'un nœud commence par une recherche : on cherche la clé du nœud à insérer ; lorsqu'on arrive à une feuille, on ajoute le nœud comme fils de la feuille en comparant sa clé à celle de la feuille : si elle est inférieure, le nouveau nœud sera à gauche ; sinon il sera à droite.

La complexité est la même que pour la recherche : O(log n) dans le cas moyen et O(n) dans le cas critique.

Pseudo code insertion , insertion par la racine

Suppression[modifier | modifier le code]

Plusieurs cas sont à considérer, une fois que le nœud à supprimer a été trouvé à partir de sa clé :

Suppression d'une feuille : Il suffit de l'enlever de l'arbre vu qu'elle n'a pas de fils.
Suppression d'un nœud avec un enfant : Il faut l'enlever de l'arbre en le remplaçant par son fils.
Suppression d'un nœud avec deux enfants : Supposons que le nœud à supprimer soit appelé N (le nœud de valeur 7 dans le graphique ci-dessous). On échange le nœud N avec son successeur le plus proche (le nœud le plus à gauche du sous-arbre droit - ci-dessous, le nœud de valeur 9) ou son plus proche prédécesseur (le nœud le plus à droite du sous-arbre gauche - ci-dessous, le nœud de valeur 6). Cela permet de garder une structure d'arbre binaire de recherche. Puis on applique à nouveau la procédure de suppression à N, qui est maintenant une feuille ou un nœud avec un seul fils.

Pour une implémentation efficace, il est déconseillé d'utiliser uniquement le successeur ou le prédécesseur car cela contribue à déséquilibrer l'arbre.

Dans tous les cas cette opération requiert de parcourir l'arbre de la racine jusqu'à une feuille : le temps d'exécution est donc proportionnel à la profondeur de l'arbre qui vaut n dans le pire des cas, d'où une complexité maximale en O(n).

Pseudo code suppression, démo complexité pire cas

Parcours ordonné[modifier | modifier le code]

On peut facilement récupérer les clés d'un arbre binaire de recherche dans l'ordre croissant en réalisant un parcours infixe. On parcourt récursivement le sous-arbre gauche, puis en ajoutant la racine, puis en parcourant récursivement le sous-arbre droit. On peut évidemment le faire dans l'ordre inverse en commençant par le sous-arbre droit.

Le parcours de l'arbre se fait en O(n), puisqu'il doit passer par chaque nœud.

Tri[modifier | modifier le code]

On peut dès lors créer un algorithme de tri simple mais peu efficace, en insérant toutes les clés que l'on veut trier dans un nouvel arbre binaire de recherche puis en parcourant de manière ordonnée cet arbre comme ci-dessus.

Le pire temps d'exécution est en O(n²), obtenu lorsque les clés sont déjà ordonnées : on obtient alors une liste chaînée. Par exemple, si on donne dans cet ordre les clés 1, 2, 3, 4, 5, on obtient l'arbre (Vide, 1, (Vide, 2, (Vide, 3, (Vide, 4, (Vide, 5, Vide))))). Il y a de nombreuses façons d'éviter ce problème, la plus commune étant l'arbre équilibré. On peut alors arriver à un pire cas en O(n ln n).

Equilibrage[modifier | modifier le code]

L'insertion et la suppression s'exécutent en O(h) où h est la hauteur de l'arbre. Il existe des techniques pour obtenir des arbres équilibrés, c'est-à-dire pour garantir une hauteur logarithmique en le nombre d'éléments :

Les arbres AVL
les arbres rouge-noir
les arbres 2-3
les arbres 2-3-4
les B-arbres

Extensions[modifier | modifier le code]

Un arbre splay est un arbre binaire de recherche qui rapproche automatiquement de la racine les éléments utilisés fréquemment. Dans un treap, chaque nœud possède aussi une priorité supérieure à chacun de ses fils.