Théorème de la sphère

En géométrie riemannienne, le théorème de la sphère montre que des informations sur la courbure d'une variété, sorte d'espace courbe à plusieurs dimensions, peuvent contraindre fortement la topologie, c'est-à-dire la forme globale de cet espace. Le théorème original est établi en 1960-61 par Marcel Berger et Wilhelm Klingenberg, comme généralisation d'un premier résultat de Harry Rauch (en) de 1951. Il a été considérablement amélioré en 2007 par Simon Brendle et Richard Schoen. Cette nouvelle version du théorème est parfois appelée théorème de la sphère différentiable.

Énoncés

L'énoncé utilise les notions de base de la topologie et de la géométrie riemannienne. Notamment, la courbure sectionnelle de la sphère de dimension n et de rayon $R$, munie de sa métrique « standard », est une constante, valant ${\frac {1}{R^{2}}}$. D'autres exemples classiques sont les métriques standard sur l'espace projectif complexe de dimension 2n, $\mathbb {C} P^{n}$ (qui est appelée métrique de Fubini-Study), l'espace projectif quaternionique de dimension 4n, et le plan projectif sur les octonions de dimension 16. Ces métriques ont une courbure comprise entre 1 et 4.

Théorème de la sphère (Berger et Klingenberg, 1959-61) — Si une variété riemannienne complète et simplement connexe a une courbure sectionnelle vérifiant ${\frac {1}{4}}<K\leq 1$ en tout point, alors elle est homéomorphe à une sphère.

Ce théorème est assorti de l'étude du cas limite

Théorème de rigidité (Berger, 1960) — Si une variété riemannienne complète et simplement connexe a une courbure sectionnelle vérifiant ${\frac {1}{4}}\leq K\leq 1$ en tout point et n'est pas homéomorphe à une sphère, alors elle est isométrique à un espace projectif (complexe, quaternionique, octonionique) muni de la métrique standard.

Brendle et Schoen ont prouvé un résultat où l'hypothèse de « pincement » entre des valeurs fixes (1/4 et 1 par exemple) est remplacée par un simple pincement ponctuel. La conclusion est également améliorée, puisqu'on obtient un difféomorphisme

Théorème de la sphère différentiable (Brendle et Schoen, 2007) — Soit M une variété riemannienne complète et simplement connexe dont la courbure sectionnelle vérifie l'hypothèse de pincement ponctuel : $0<K(P_{1})<4K(P_{2})$ pour tout point m et tout couple de 2-plans de l'espace tangent en m. Alors M est difféomorphe à la sphère standard.

Histoire de la preuve

Le théorème de la sphère classique

Dans la première démonstration du théorème de la sphère, Harry Rauch fait une comparaison avec la façon dont une bourse se replie sur elle-même grâce à son cordon.

Le théorème de la sphère se place dans un grand mouvement de recherche de liens entre la métrique d'une variété riemannienne et sa topologie. Le théorème de la sphère est le premier résultat dans lequel on obtient un encadrement des propriétés métriques avec des bornes inférieure et supérieure. Ainsi un résultat précédent, le théorème de Bonnet-Schoenberg-Myers de 1935, assure une majoration du diamètre sous hypothèse que la courbure est minorée mais ne donne pas d'information liée à la minoration.

Heinz Hopf, qui a finalisé en 1926 la classification des variétés à courbure sectionnelle constante, émet la conjecture qu'une variété simplement connexe à courbure très proche de 1 doit encore être une sphère. En 1951, Harry Rauch apporte une preuve de cette conjecture. Ce premier résultat est proche de l'énoncé du théorème de la sphère, mais avec une constante non optimale, de l'ordre de 3/4. Pour cela il montre qu'on peut décomposer la variété en une « sphère géodésique » (image d'une sphère par l'application exponentielle) de rayon proche de $\pi$ et une partie résiduelle, qu'il arrive à décrire suffisamment pour montrer qu'elle est contractile, comme lors de la fermeture d'une bourse.

Wilhelm Klingenberg donne un nouvel outil d'étude en apportant une borne sur le rayon d'injectivité, lorsqu'on a une majoration sur la courbure. Il prouve ce résultat d'abord dans le cas des variétés de dimension paire en 1959, puis il étend son résultat à tout type de variété en 1961. Entre-temps Marcel Berger a utilisé les résultats de Klingenberg pour prouver le théorème de la sphère. Celui-ci sera publié en 1960 pour les variétés de dimension paire, mais l'amélioration du résultat de Klingenberg s'est automatiquement transférée au théorème de la sphère en 1961. Le principe général de la démonstration est d'introduire deux points p,q d'éloignement maximum (leur distance est égale au diamètre) et de montrer que la variété est recouverte par deux boules géodésiques, l'une centrée en p et l'autre en q, dès lors que les rayons sont choisis judicieusement.

À la recherche d'un théorème différentiable

Dans les décennies qui suivent sa publication, diverses améliorations du théorème de la sphère sont apportées, dans différentes directions. De nombreux résultats sont publiés avec des variantes de l'hypothèse de pincement, variantes qui contiennent parfois une spécification sur la dimension. Certains résultats permettent de pousser au-delà du facteur limite 1/4, en incluant les espaces projectifs dans les topologies caractérisées. Il y a également des versions du théorème, dites équivariantes, qui permettent de traiter le cas des variétés non simplement connexes.

Enfin une des directions de recherche principales a été l'établissement d'une version du théorème avec caractérisation de la topologie en termes de difféomorphisme. En effet, on sait depuis 1957 qu'il existe des sphères exotiques, c'est-à-dire la possibilité de trouver un certain nombre de structures différentielles autres que la structure standard sur la sphère topologique de dimension n. Il convient donc de savoir si ces variétés peuvent admettre des métriques vérifiant la condition de pincement.

Ce problème a été attaqué dans deux directions : d'une part, en partant des sphères exotiques, chercher à voir quelles conditions on peut imposer à la métrique : on sait ainsi construire un exemple de sphère non standard mais à courbure sectionnelle positive, ce qui ne rapproche qu'en partie de la propriété de pincement. D'autre part, une version du théorème de la sphère avec une conclusion plus large a été recherchée. Elle n'a d'abord été obtenue qu'avec une constante de pincement non optimale par Gromoll et Calabi en 1966. D'autres chercheurs ont peu à peu amélioré la constante dans les années 1960 et 1970, mais elle est restée loin de la valeur 1/4.

Du flot de Ricci au théorème de la sphère différentiable

Avec le flot de Ricci, on déforme la métrique continûment en espérant qu'elle se rapproche d'une métrique modèle simple.

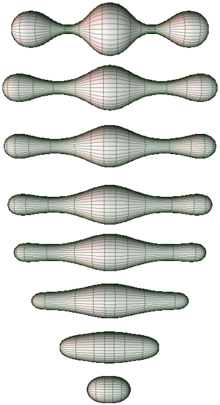
Introduction du flot de Ricci et résultats en petite dimension

Depuis les années 1980, des idées nouvelles ont été mises en œuvre avec succès pour déformer continûment des métriques afin de les « lisser » pour les rapprocher de métriques modèles. Le procédé emblématique est le flot de Ricci, qui consiste à modifier la métrique suivant une équation d'évolution faisant intervenir la courbure de Ricci : $\partial _{t}g_{t}=-2\mathrm {Ric} (g_{t})$. En introduisant ce nouveau procédé Richard Hamilton se fixe pour objectif de progresser vers une compréhension de la topologie des variétés, en visant notamment la résolution de la célèbre conjecture de Poincaré, qui de fait sera résolue en 2003 grâce à cet outil. Le flot de Ricci est également l'outil principal de la preuve du théorème de la sphère différentiable.

Le premier grand succès de la théorie a été de montrer qu'une variété de dimension 3 à courbure de Ricci strictement positive évolue vers une métrique de courbure constante, en 1982, ce qui constitue une version très forte du théorème de la sphère, mais limitée à la dimension 3. Deux ans après , un résultat analogue est établi pour les variétés de dimension 4 à opérateur de courbure strictement positif. Cette condition de positivité n'entraîne pas pour autant la condition de pincement 1/4 mentionnée dans le théorème de la sphère de 1960. Chen prouvera en 1991, toujours en employant le flot de Ricci, qu'on peut écrire ce théorème de la sphère pour les variétés de dimension 4 en concluant au difféomorphisme.

Le théorème différentiable

Un ingrédient important de la preuve du théorème différentiable de Brendle et Schoen est l'introduction de la notion de courbure isotrope et de la condition de courbure isotrope strictement positive (couramment abrégée sous la forme PIC). Cette condition peut être formulée sur le tenseur de courbure : les composantes dans une base orthonormale $(e_{1},e_{2},e_{3},e_{4})$ vérifient

$R_{1313}+R_{1414}+R_{2323}+R_{2424}-2R_{1234}>0.$

L'intérêt est que l'hypothèse de pincement 1/4 ponctuel entraîne cette condition PIC. On peut donc chercher quelles conclusions cette condition entraîne.

Micallef et Moore l'introduisent pour la première fois en 1988 ; ils prouvent, à l'aide de la théorie des surfaces minimales, qu'une variété compacte simplement connexe vérifiant la condition PIC est homéomorphe à la sphère. Hamilton montre en 1997 que le flot de Ricci conserve la condition PIC (au sens large) pour les variétés de dimension 4 et il établit un résultat de classification à difféomorphisme près sous cette condition. Dans leur preuve de 2007, Brendle et Schoen montrent que la condition PIC (au sens large) est préservée par le flot de Ricci en toute dimension. De plus, ils ont trouvé de nouvelles conditions telles que PIC1 et PIC2 qui sont préservées sous le flot.

Dans un article de 2006, Christoph Böhm et Burkhard Wilking ont prouvé qu'une variété riemannienne compacte une métrique d'opérateur de courbure strictement positif évolue par flot de Ricci (renormalisé) vers une métrique à courbure constante. Néanmoins les hypothèses « pincement ponctuel 1/4 » et « opérateur de courbure strictement positif » entraînent toutes les deux la propriété PIC2 mais ne s'entraînent pas l'une l'autre. Surtout, Böhm et Wilking introduisent, par une utilisation judicieuse du principe du maximum, une notion de famille de cônes de plus en plus pincés dans lesquels on localise l'opérateur de courbure, ce qui permet d'en maîtriser l'évolution.

Brendle et Schoen s'appuient sur l'approche de flot de Ricci pour prouver le théorème de la sphère différentiable. Ils construisent une famille de cônes adaptée à l'hypothèse PIC2 et montrent qu'une variété riemannienne compacte une métrique satisfaisant à la condition PIC2 évolue par flot de Ricci vers une métrique à courbure constante. Comme pincement-1/4 implique la condition PIC2, le théorème de la sphère différentiable suit en conséquence. Un des avantages de la démarche suivie est que la déformation de la métrique se fait de façon compatible avec l'action du groupe orthogonal, donc le théorème de la sphère différentiable possède de façon naturelle une version équivariante. Un an après la publication du théorème, Brendle et Schoen le complètent par une étude du cas limite généralisant le théorème de rigidité de Berger en termes de difféomorphismes. Ils emploient pour cela une forme forte du principe du maximum pour une équation aux dérivées partielles elliptique dégénérée.

Bibliographie

• (en) Marcel Berger, A Panoramic View of Riemannian Geometry, 2003 [détail de l’édition], p. 552-568 — L'ouvrage de Marcel Berger paru en 2003 décrit l'histoire du théorème de la sphère et les nombreuses avancées qui ont suivi, avant que la version différentiable ne vienne profondément modifier la situation.
• (en) Simon Brendle et Richard Schoen, « Curvature, Sphere Theorems, and the Ricci Flow », Bull. Amer. Math. Soc., vol. 48, n^o 1,‎ 2011, p. 1-32 (DOI 10.1090/s0273-0979-2010-01312-4, MR 2738904, arXiv 1001.2278)
• (en) Ben Andrews et Christopher Hopper, The Ricci Flow in Riemannian Geometry: A Complete Proof of the Differentiable 1/4-Pinching Sphere Theorem, Lecture Notes in Mathematics, Springer, 2011