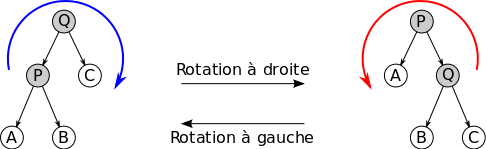
Rotation d'un arbre binaire de recherche

En algorithmique, la rotation d'un arbre binaire de recherche permet de changer la structure d'un arbre binaire de recherche ou ABR sans invalider l'ordre des éléments. Une telle rotation consiste en fait à faire remonter un nœud dans l'arbre et à en faire redescendre un autre.

Cette opération est très utilisée dans les arbres équilibrés en général car elle permet de réduire la hauteur d'un arbre en faisant descendre les petits sous-arbres et remonter les grands, ce qui permet de « rééquilibrer » les arbres et d'accélérer de nombreuses opérations sur ces arbres.

Illustration

L'opération de rotation droite telle qu'elle apparaît dans l'image ci-dessus est réalisée en utilisant Q comme racine. C'est donc une rotation droite sur Q. Elle aboutit à une rotation de l'arbre dans le sens des aiguilles d'une montre. L'opération inverse est une rotation gauche, qui aboutit à un mouvement dans le sens inverse des aiguilles d'une montre (la rotation gauche ci-dessus est réalisée sur le nœud P).

La compréhension de la rotation passe par la compréhension de ses contraintes. En particulier l'ordre des feuilles de l'arbre (lorsqu'elles sont lues de gauche à droite par exemple) ne peut pas changer (autrement dit, lors d'un parcours en profondeur, l'ordre de visite des feuilles est le même qu'avant l'opération). L'autre contrainte est la propriété principale d'un arbre binaire de recherche, c'est-à-dire que le fils gauche est plus petit que son père et que le fils droit est plus grand que son père.

Comme on peut le voir dans le diagramme, l'ordre des feuilles ne change pas. L'opération opposée préserve aussi l'ordre et est le deuxième type de rotation.

En supposant que c'est un arbre binaire de recherche, les éléments doivent être interprétés comme des variables qu'on peut comparer les unes aux autres. Les lettres de l'alphabet ci-dessus sont de telles variables.

Algorithme

Quand un sous-arbre subit une rotation, la hauteur de l'un de ses côtés augmente et celle de l'autre côté diminue. Ceci rend les rotations utiles pour équilibrer un arbre.

On utilisera la terminologie de Racine pour le nœud père du sous-arbre qui subit la rotation, Pivot pour le nœud qui devient le nouveau père, Nœud→CR pour le fils d’un nœud donné du côté de la rotation et Nœud→CO pour le fils du côté opposé. On distingue la rotation droite et la rotation gauche. Dans la première, CR désigne le fils droit d’un nœud et CO le fils gauche ; dans la seconde, c’est le contraire. Le pivot est le CO initial de la racine.

Dans le diagramme ci-dessus, pour la racine Q et la rotation droite, le CR est C et le CO est P. Le pseudo-code de la rotation est :

Pivot     = Racine→CO
Racine→CO = Pivot→CR
Pivot→CR  = Racine
Racine    = Pivot

C'est une opération en temps constant.

Le programmeur doit s'assurer que le père de la racine du sous-arbre pointe vers le pivot après la rotation (la dernière ligne dans le pseudo-code ci-dessus).

En lisant ce pseudo-code, la rotation apparaît clairement : le pivot désigne le CO initial de la racine, puis celui-ci contient le CR initial du pivot, qui devient ensuite la racine initiale, cette dernière devenant enfin le pivot.

Exemples

L'arbre

        E
       / \
      /   \
     /     \
    B       F
   / \
  /   \
 A     D
      /
     C

peut subir une rotation et devenir ainsi :

     B
    / \
   /   \
  /     \
 A       E
        / \ 
       D   F 
      /
     C

C’est une rotation droite (de racine E). L'opération inverse est la rotation gauche. Notons que le nœud D, le fils droit de B, a changé de père.

On peut aussi obtenir la forme alternative suivante :

      D
     / \
    /   \
   B     E
  / \     \
 A   C     F

en effectuant deux rotations successives :

         E                                    E                                    D       
        / \                                  / \                                  / \      
       /   \                                /   \                                /   \     
      /     \                              /     \                              /     \    
     B       F    rotation gauche         D       F    rotation droite         B       E   
    / \           -------------->        /             -------------->        / \       \  
   /   \            de racine B         /                de racine E         /   \       \ 
  A     D                              B                                    A     C       F
       /                              / \                                                  
      C                              A   C                                                 

Ici, on a fait remonter le nœud D, qui a « adopté » son père B (B a adopté C, le fils gauche de D) puis son grand-père E (D n’avait pas de fils droit, sinon E l’aurait adopté).

Liens externes

• (en) Un applet montrant des rotations