Utilisateur:Salle/Brouillon
En géométrie, une conique est une courbe algébrique plane. Du point de vue algébrique, il s'agit des courbes les plus simples en dehors des droites. Dans un certain sens, elles généralisent la notion de cercle dans des espaces sans structure métrique. Elles ont été étudiées dès l'Antiquité, notamment par Apollonius de Perga à qui est dû un Traité des coniques, datant du IIIe siècle av. J.-C..
Elles peuvent être étudiées de plusieurs point de vue. Les exposés modernes privilégient une démarche partant de la géométrie projective, modélisée par l'algèbre linéaire sur un corps de caractéristique différente de 2 : les coniques non dégénérées sont alors toutes isomorphes (sur un corps algébriquement clos) ; c'est l'exposé dans lequel la classification est la plus simple, mais il demande un outil mathématique peu enseigné dans les niveaux d'études élémentaires. L'exposé affine s'en déduit alors facilement. Dans le cas où le corps de base est le corps des nombres réels, c'est dans ce cadre qu'on retrouve les notions d'ellipse, de parabole et d'hyperbole, qui sont utiles notamment en géométrie céleste. L'exposé antique d'Appolonius distinguait ces divers types de coniques, mais par une voie différente, provenant purement de la géométrie d'incidence : elles sont obtenues comme sections planes d'un cône de révolution, et le type varie suivant l'inclinaison du plan par rapport au cône. Enfin, si une structure euclidienne est ajoutée à l'espace, les coniques d'un même type sont différenciées par des quantités métriques, notamment l'excentricité.
Point de vue linéaire[modifier | modifier le code]
En géométrie affine[modifier | modifier le code]
Dans un plan affine sur un espace vectoriel V, si une fonction du plan à valeurs dans le corps des scalaires est un polynôme de degré 2 en les coordonnées de ce point dans un repère affine fixé, alors c'est encore une fonction polynomiale de degré 2 en les coordonnées dans tout autre repère. Une telle fonction est appelée polynôme du plan affine. Une conique est définie comme une classe d'équivalence, pour la relation de multiplication par un scalaire non nul, de telles fonctions ; il s'agit donc d'une définition indépendante du repère. L'image d'une conique est l'ensemble des points dont les coordonnées annulent le polynôme. Un tel polynôme s'écrit :
où x=(x1,x2) désigne un couple de scalaires représentant les coordonnées des points du plan affine dans un repère fixé, q est une forme quadratique, l une forme linéaire, et c un scalaire. La classification des coniques s'appuie sur la classification des formes quadratiques : pour tout polynôme P(x) de degré 2, il existe un scalaire a, une forme quadratique q et un repère dans lequel la fonction ait une des trois formes suivantes :
Plus précisément, dans le premier et le troisième cas, la forme quadratique q peut être choisie parmi un système de représentants des classes d'équivalence pour l'action conjointe du groupe linéaire et du groupe multiplicatif du corps des scalaires , et dans le deuxième cas, il en est de même avec l'action . Qui plus est.........
En géométrie projective[modifier | modifier le code]
Dans le cas d'un plan projectif, une conique est une classe d'équivalence de polynômes homogènes non nuls de degré 2 en trois variables x, y et z (donc de la forme P(x,y,z)=axxx2+ayyy2+azzz2+2axyxy+2axzxz+2ayzyz , c'est-à-dire des formes quadratiques) pour la relation de colinéarité :
D'un point de vue géométrique, l'image de la conique (un point dans cette image est simplement appelé point de la conique) est alors l'ensemble des points dont les coordonnées homogènes [x:y:z], dans un repère projectif fixé, vérifient P(x,y,z) (et c'est indépendant du représentant P de la classe d'équivalence choisi). Une conique est dite propre ou non dégénérée si la forme quadratique la définissant est non dégénérée (donc de rang 3). L'image d'une conique propre est soit vide, soit isomorphe à la droite projective, comme expliqué ci-dessous. Dans le cas d'une conique de rang 2, elle peut être réduite à un point, ou être constituée de deux droites sécantes. Enfin, l'image d'une conique de rang 1 est une droite.
La tangente à une conique en un point [x0,y0,z0] non singulier de son image est la droite d'équation :
Il s'agit d'une droite passant par le point de coordonnées [x0:y0:z0], plus précisément de l'orthogonal de ce point pour la forme quadratique définissant la conique. Dans le cas d'une conique propre, c'est l'unique droite passant par ce point ne coupant pas la conique en un autre point. Par ailleurs, toutes les autres droites passant par ce point ont un unique autre point d'intersection avec la conique. La notion de tangente en un point de l'image se généralise pour tout point de l'espace projectif : à un tel point est associée sa polaire, qui est l'ensemble des points qui lui sont orthogonaux pour la forme quadratique définissant la conique.

Ce fait a pour conséquence qu'une conique non dégénérée peut être paramétrée par la droite projective. Les droites passant par un point fixé forment un faisceau. Outre la tangente, une autre droite passant par le point M=[x0:y0:z0] est fixée, dont l'équation est notée x1x+y1y+z1z. Alors l'espace des équations des droites passant par M est paramétré par :
La paramétrisation de la conique est alors obtenue en associant à une droite son autre point d'intersection avec la conique (le point M lui-même dans le cas tangent, c'est-à-dire pour les valeurs des paramètres s=0). Par exemple, dans le cas de la conique d'équation x2+y2-z2, pour le point M=[1:0:1], et en prenant (x1,y1,z1)=(0,1,0), la paramétrisation ci-dessus devient :
Aux coordonnées [1:t] est alors associé le point d'intersection de la conique x2+y2-z2=0 et de la droite tx+y-tz=0. Dans le plan affine d'équation z=1, la résolution d'une équation du second degré fournit la solution , pour toute valeur de t. On reconnaît le paramétrage du cercle unité dans un plan affine euclidien. Le paramétrage projectif est .
Passage du projectif à l'affine[modifier | modifier le code]

Un plan affine est obtenu comme un plan projectif auquel une droite, appelée « droite à l'infini », a été ôtée. D'un point de vue analytique, il s'agit de se placer dans une carte, par exemple de ne considérer que les points dont les coordonnées ont la forme [x:y:1]. L'équation d'une conique projective devient alors une classe d'équivalence de polynômes en deux variables de degré 2 (par exemple en posant z=1 dans l'équation projective). Si P est un représentant de cetet classe, l'image de la conique affine est l'ensemble des couples (x,y) tels que P(x,y)=0. Comme dans le cas projectif, la classification des coniques affines dépend du corps considéré. Le cas du corps des réels est le plus classique, une conique affine non dégénérée d'image non vide peut être de trois types :
- si la droite à l'infini ne coupe pas l'image de la conique projective, la conique affine est une ellipse.
- si le droite à l'infini est une tangente à la conique projective, la conique affine est une parabole (dont l'axe admet pour direction celle du point de tangence à l'infini).
- si la droite à l'infini est une sécante à la conique projective, la conique affine est une hyperbole (dont les directions asymptotiques sont données par les points à l'infini).
Le pôle de la droite à l'infini pour une hyperbole ou une ellipse (c'est-à-dire le point qui est orthogonal à tous les points de la droite à l'infini pour la forme quadratique définissant la conique projective) est appelé centre de la conique affine.
Définition par section d'un cône[modifier | modifier le code]
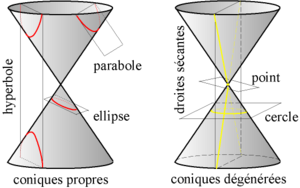
Selon les positions relatives du plan et du cône, on obtient différents types de coniques :
- les coniques propres, quand le plan n'est pas perpendiculaire à l'axe du cône, et ne passe pas par son sommet. On distingue trois sortes de coniques propres en fonction de l'angle d'inclinaison du plan avec l'axe du cône :
- les coniques partiellement dégénérées :
- l'intersection est un cercle quand le plan est perpendiculaire à l'axe du cône;
- l'intersection est une hyperbole équilatère quand l'angle d'inclinaison du plan est inférieur de 45° à l'angle d'ouverture du cône;
- et les coniques totalement dégénérées, quand le plan contient le sommet du cône :
- l'intersection est un couple de droites sécantes, si l'angle d'inclinaison du plan avec l'axe du cône est inférieur à l'angle d'ouverture du cône ;
- l'intersection est réduite à une droite si ces angles sont égaux.
- enfin elle est réduite à un point si l'angle d'inclinaison est supérieur à l'angle d'ouverture.
Définition monofocale[modifier | modifier le code]
La définition monofocale des coniques est encore appelée définition par foyer et directrice de ces coniques.
Définition[modifier | modifier le code]
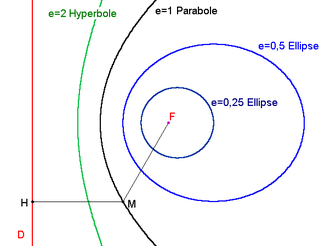
Dans un plan (p), on considère une droite (d) et un point non situé sur (d). Soit un réel strictement positif.
On appelle conique de droite directrice (d), de foyer et d'excentricité l'ensemble des points du plan (p) vérifiant :
où
- mesure la distance du point M au point F
et
- mesure la distance du point M à la droite (d)
On notera que les ellipses sont des courbes fermées et bornées, que les paraboles sont ouvertes et infinies, et que les hyperboles possèdent deux branches symétriques par rapport au point d'intersection de leurs asymptotes communes.
Mise en équation[modifier | modifier le code]
Soit O la projection orthogonale du point F sur la droite (d). Dans le plan (p) on définit alors le repère orthogonal (O, (OF), (d)).
Soit p la distance de O à F (p s'appelle le paramètre). Dans le repère défini précédemment F a pour coordonnées (p,0).
Pour un point M de coordonnées on peut exprimer les distances précédentes à l'aide des deux formules suivantes :
ce qui implique en élevant [1] au carré et en utilisant [2] et [3] :
soit après simplification :

En fonction des valeurs de e on obtient plusieurs types de courbes :
Les coniques dégénérées s'obtiennent en modifiant les conditions précédentes
- Si F est sur D, on obtient :
- Si le point O (qui est aussi le point F);
- Si la droite perpendiculaire à (d) passant par F;
- Si deux droites sécantes ;
- Si , le point O (qui est aussi le point F).
Il n'existe donc pas de définition de cercle par foyer et directrice. En revanche, si pe = r et si e tend vers 0 (ce qui augmente à l'infini la distance entre le foyer et la directrice), l'ellipse se rapproche d'un cercle de centre F et de rayon r
Définition bifocale[modifier | modifier le code]
L'ellipse peut être définie comme le lieu des points dont la somme des distances à deux points fixes appelés foyers de l'ellipse est constante et égale à une valeur fixée. Cette définition reste valable dans le cas du cercle, dans lequel les foyers sont confondus.
L'hyperbole peut être définie comme le lieu des points dont la valeur absolue de la différence des distances à deux points fixes appelés foyers de l'hyperbole est constante et égale à une valeur fixée.
La parabole n'a pas de définition bifocale.
Définition analytique[modifier | modifier le code]
Cas affine[modifier | modifier le code]
En géométrie analytique affine, les coniques sont les courbes planes algébriques du second ordre, c'est-à-dire les courbes planes dont les coordonnées cartésiennes x et y des points sont solution d'une équation polynômiale du second degré, de la forme :
avec l'un au moins des trois coefficients A, B ou C non nul pour que l'équation soit effectivement du second degré ( condition (1) ).
Suivant le repère utilisé, l'expression de l'équation sera plus ou moins simple, mais restera toujours du second degré. Il est intéressant de chercher le repère dans lequel l'expression de l'équation, dite équation réduite, sera la plus simple.
Pour cela, nous pouvons remarquer d'abord qu'il est toujours possible de rendre le coefficient B nul par une rotation du repère.
Nous regardons ensuite les coefficients A et C :
- Si le coefficient C est lui aussi nul, A est alors forcément non nul ( condition (1) ), et une translation suivant l'axe des x permet ainsi d'annuler le coefficient D.
- Si E est nul, en posant p = - F / A , l'équation se réduit à :
- Suivant le signe de p, nous obtenons 0 à 2 droites parallèles.
- Si E est non nul, une translation suivant l'axe des y annule F. En posant p = - A / E , nous obtenons l' équation cartésienne réduite d'une PARABOLE :
- Si le coefficient A est nul, on obtient la situation symétrique de la précédente où x et y voient leurs rôles échangés. On obtient donc encore :
- Si D est nul, 0 à 2 droites parallèles,
- Si D est non nul, une PARABOLE d'équation réduite :
- Si les coefficients A et C sont tous les deux non nuls, une translation suivant l'axe des x annule D, et une translation suivant les y annule E. L'équation se réduit donc à :
- Si A et C sont de même signe :
- - si F est lui aussi du même signe, il n'y a pas de courbe correspondante;
- - si F est nul, la courbe se réduit à un point;
- - si F est de signe opposé, nous pouvons poser a 2 = - F / A et b 2 = - F / C ; nous parvenons ainsi à l' équation cartésienne réduite d'une ELLIPSE :
- Si A et C sont de signes opposés :
- - si F est nul, la courbe se réduit à 2 droites sécantes (= qui se croisent);
- - si F est du signe de A, nous pouvons poser a 2 = F / A et b 2 = - F / C ; nous parvenons ainsi à l' équation cartésienne réduite d'une HYPERBOLE :
- - si F est du signe de C, nous pouvons poser a 2 = - F / A et b 2 = F / C ; nous parvenons ainsi à l' autre équation cartésienne réduite d'une HYPERBOLE :
Cas projectif[modifier | modifier le code]
En géométrie analytique projective, les coniques sont encore les courbes planes algébriques du second ordre, c'est-à-dire les courbes planes dont les points ont des coordonnées projectives X, Y et Z qui vérifient une équation polynômiale homogène du second degré de la forme (voir coordonnées homogènes):
On travaille donc dans le plan projectif où un point générique a pour coordonnées homogénes , et deux coordonnées homogènes proportionnelles ( et , pour un certain ) désignent le même point du plan. Notre plan projectif contient plusieurs exemplaires du plan affine ; notamment l'ensemble des points admettant des coordonnées homogènes de la forme .
On peut noter alors que pour Z = 1, on retrouve l'équation du cas affine. En fait, on a :
et
Une première question qu'on se pose est alors : en se limitant à l'image de la conique dans le plan affine ci-dessus défini, quel type de conique affine retrouve-t-on? (et même, retrouve-t-on bien une conique affine?). Pour ce faire, on regarde d'abord leur comportement à l'infini (présence d'asymptotes ou de branches paraboliques,...). Faire tendre x et y vers l'infini revient à faire tendre Z vers 0. Pour Z = 0, l'équation précédente se réduit à :
Cette équation est appelée équations aux directions asymptotiques, car le rapport Y / X donne alors la pente à l'infini de la courbe, c'est-à-dire sa direction asymptotique.
- Si C = 0 :
- si B = 0 , l'équation a une solution X = 0 de multiplicité double, ce qui correspond à une pente à l'infini infinie, donc à une direction asymptotique verticale double; la courbe est donc soit une parabole d'axe vertical, soit 0 à 2 droites verticales parallèles;
- si B est non nul, nous obtenons deux directions asymptotiques simples, l'une verticale, l'autre non; la courbe est donc soit une hyperbole, soit 2 droites concourantes;
- Si C est non nul, en posant t = Y / X, l'équation devient :
- si le discriminant de cette équation est strictement positif, nous obtenons 2 directions asymptotiques simples distinctes, et la courbe est soit une hyperbole, soit 2 droites concourantes;
- si le discriminant de cette équation est nul, nous obtenons une direction asymptotique double, et la courbe est soit une parabole, soit 0 à 2 droites parallèles;
- si le discriminant de cette équation est strictement négatif, la courbe n'a pas de direction asymptotique, donc pas de branches infinies, et la courbe, si elle existe, est soit une ellipse, soit un point.
Cependant, le véritable intérêt de l'utilisation de la géométrie projective est ailleurs. La classification qui a été faite dans le cas affine, et réinterprétée dans le cadre projectif, se base sur des changements de coordonnées affines ; et qui peuvent s'interpréter, le plan affine étant vu comme une partie du plan projectif, comme les changements de coordonnées projectifs qui laissent fixe la droite à l'infini (c'est-à-dire les points du plan projectif de la forme ). Il existe évidemment beaucoup d'autres changements de coordonnées projectifs, et s'autoriser à les utiliser va permettre d'assouplir grandement la classification des coniques. En fait, la classification des coniques projectives provient directement de celle des forme bilinéaire symétrique sur l'espace vectoriel de dimension 3 sous-jacent à notre plan projectif.
Cas barycentrique[modifier | modifier le code]
En géométrie analytique barycentrique, les coniques sont toujours les courbes planes algébriques du second ordre, c'est-à-dire les courbes planes dont les points ont des coordonnées barycentriques λ, μ et ν qui vérifient une équation polynômiale homogène du second degré de la forme :
On peut identifier cette équation à la précédente, en posant :
On obtient alors, à un coefficient multiplicatif près :
Liens entre les définitions[modifier | modifier le code]
Définition monofocale et définition bifocale[modifier | modifier le code]
Les paraboles admettent un et un seul couple foyer/directrice au sens de la définition monofocale, et l'excentricité correspondante vaut 1.
Ellipses et hyperboles admettent exactement deux couples foyer/directrice au sens de la définition monofocale, et ceux-ci correspondent à une même valeur de l'excentricité. Ils sont symétriques par rapport au centre de l'ellipse ou au point d'intersection des asymptotes de l'hyperbole. Ces foyers sont les points intervenant dans la définition bifocale.
Définition géométrique et définition bifocale[modifier | modifier le code]
Les foyers et les directrices des coniques peuvent être déterminés géométriquement dans le cadre de la définition des coniques comme intersection d'un cône et d'un plan ne passant pas par le centre de celui-ci.
Il existe, selon l'orientation du plan par rapport à l'axe du cône, une (cas des paraboles) ou deux (cas des ellipses et des hyperboles) sphères tangentes à la fois au plan et au cône; ce sont des sphères centrées sur l'axe, situées dans un même demi-cône (cas des ellipses) ou dans des demi-cônes opposés (cas des hyperboles).
Chacune de ces sphères définit l'un des foyers de la conique (c'est le point de tangence de la sphère et du plan) ainsi que la droite directrice associée (c'est l'intersection du plan de la conique et du plan contenant le cercle de tangence de la sphère et du cône).







![{\displaystyle [s:t]\mapsto \left(sx_{1}+t{\frac {\partial P}{\partial x}}(M)\right)x+\left(sy_{1}+t{\frac {\partial P}{\partial y}}(M)\right)y+\left(sz_{1}+t{\frac {\partial P}{\partial z}}(M)\right)z.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604941030b5d89ff6bde7fc9e8682a2790a8a435)
![{\displaystyle [s:t]\mapsto tx+sy-tz.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f6b9d4226825b3713cbc00fa32267a8c50fbae5)
![{\displaystyle [{\frac {t^{2}-1}{t^{2}+1}}:{\frac {2t}{t^{2}+1}}:1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a64311e053b06727fe854dbcad0f6ab3a63fff4f)
![{\displaystyle [s:t]\mapsto [t^{2}-s^{2}:2ts:t^{2}+s^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bc6696ce64360665d138e2fcbd2d03bfa67b491)



![{\displaystyle [1]\ d(M,F)=e\ d(M,(d))\qquad e\in \mathbb {R} _{+}^{*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/894556b5883d996388c2a94aea8d26337936c80d)



![{\displaystyle [2]\qquad d(M,F)={\sqrt {(x-p)^{2}+(y-0)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7c647eb9bd1a8e46ed8ffc6ded56873b1429d54)
![{\displaystyle [3]\qquad d(M,(d))={\sqrt {(x-0)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86761bf11020b757c40c6cf533a6858bdd294328)
![{\displaystyle [4]\qquad (x-p)^{2}+y^{2}=e^{2}x^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b091f80a00203f8c7234f618245964d2a78c2cb)
![{\displaystyle [5]\qquad x^{2}(1-e^{2})+y^{2}-2xp+p^{2}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53c7abbf50d3925f82b951eb649df53f68dbfe65)














![{\displaystyle [X:Y:Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b4c3e5530dea19af82c91a458eb9975ab3b90ce)
![{\displaystyle [\lambda X:\lambda Y:\lambda Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61a7059b1f956ac3de6e740f9882cd54461c5588)

![{\displaystyle [X:Y:1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a9ac370164b345b9a0f53cd05012c1833a5b5b5)




![{\displaystyle [X,Y,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c691adce48f5c8245cf3a51e5c8824f303c9523e)


