Utilisateur:Démosthène/Brouillon/Traduction de Polarization

Réécriture

Exemple de banc de polarisation

La polarisation est une propriété des ondes, au même titre que la phase et la fréquence. Il s'agit d'une caractéristique propre aux ondes vectorielles dont font par exemple partie les ondes électromagnétiques telles que la lumière ou les ondes gravitationnelles. En revanche, les ondes mécaniques telles que les ondes sonores ne sont pas concernées.

Dans une onde électromagnétique, le champ électrique et le champ magnétique oscillent simultanément dans des directions différentes. La polarisation de la lumière est la grandeur qui décrit le comportement du champ électrique. Ce champ peut osciller dans une seule direction (polarisation rectiligne) ou peut tourner autour de l'axe de propagation de l'onde (polarisation circulaire ou elliptique). Le sens de la rotation, droite ou gauche, est également un paramètre clé lié à la biréfringence et à l'activité optique des milieux traversés.

La polarisation des ondes occupe un place importante dans de nombreux domaines scientifiques tels que l'optique, la séismologie, l'étude des ondes radiofréquences et micro-ondes. Les technologies concernée sont plus particulièrement les lasers, les télécommunications (fibrées ou non) et les radars.

Théorie

Hypothèses de départ

La plupart des sources de lumière sont incohérentes et dépolarisées (ou partiellement polarisées). Ces sources émettent un mélange d'ondes dont les propriétés spatiales et temporelles (telles que la phase, la longueur d'onde et la polarisation) sont aléatoires. Ces sources étant difficile à étudier, on simplifie dès le départ le problème.

Onde plane

Pour bien comprendre les ondes magnétiques et la polarisation, le moyen le plus simple est de considérer des ondes planes et cohérentes. Ces ondes sont sinusoïdales et peuvent être décrites par un vecteur d'onde, un fréquence, une phase et un état de polarisation uniques.

Le formalisme décrivant la polarisation s'appuie sur le modèle de l'onde plane cohérente. En optique, caractériser un système avec une telle onde permet de déduire ensuite le comportement du système avec des ondes moins simples. En effet, le théorème de superposition permet de décomposer n'importe quelle onde complexe en une somme d'ondes élémentaires. Cette décomposition est désignée par le terme de spectre angulaire. Ainsi, une onde réelle sera modélisée par une somme d'ondes planes décorrélées dont la phase et la fréquences seront réparties aléatoirement; même en travaillant avec des ondes très simples, on peut décrire in fine des ondes beaucoup plus compliquées.

Ondes transverses électrique (TE)

Une onde électromagnétique se propageant dans l'espace libre (ou tout autre milieu homogène, isotrope et transparent) peut-être qualifiée d'onde transverse. Cela signifie que ses vecteurs E de champ électrique et H de champ magnétique sont dans un plan orthogonal à la direction de propagation. De plus, les champs E et H sont orthogonaux entre eux. En choisissant une telle onde monochromatique se propageant selon l'axe z, on oblige E et H à être dans le plan défini par x et y. Pour décrire la phase, il est de plus d'usage d'utiliser une notation en nombres complexes. Les champs réels E et H correspondent alors aux parties réelles de ces notations. En notant de plus t le temps, les ondes sont décrites par:

${\vec {E}}(z,t)={\begin{bmatrix}e_{x}\\e_{y}\\0\end{bmatrix}}\;e^{i(kz-\omega t)}$

and

${\vec {H}}(z,t)={\begin{bmatrix}h_{x}\\h_{y}\\0\end{bmatrix}}\;e^{i(kz-\omega t)}$

avec k la norme du vecteur d'onde et ω sa période. Cette expression rend compte à la fois de la dépendance temporelle et spatiale de l'onde.

De plus, E et H sont toujours orthogonaux, donc leur produit scalaire est nul.

${\vec {E}}({\vec {r}},t)\cdot {\vec {H}}({\vec {r}},t)=0$

Sachant qu'ils n'ont que des composantes selon x et y, l'équation précédente se résume à:

$e_{x}h_{x}+e_{y}h_{y}=0$

De plus, pour un milieu d'impédance η, e et h sont reliés par:

$h_{y}=e_{x}/\eta$

and

$h_{x}=-e_{y}/\eta$

Les coefficients ex et ey suffisent pour définir un état de polarisation. Dans le formalisme de Jones, l'état de polarisation de l'onde est décrite sous la forme d'un vecteur colonne à deux composantes (ex et ey), généralement complété par l'amplitude et la phase de l'onde.

Actuel sur WP français

Exemple de banc de polarisation

La polarisation est une propriété des ondes vectorielles, c'est-à-dire pouvant osciller selon plus d'une orientation. Les ondes électromagnétiques telles que la lumière ou les ondes gravitationnelles ont ainsi des propriétés de polarisation tandis que les ondes mécaniques (telles que les ondes sonores) ne sont pas concernées.

Dans une onde électromagnétique, le champ électrique et le champ magnétique oscillent simultanément dans des directions différentes. Par convention, la polarisation de la lumière décrit la vibration du champ électrique. Ce champ peut osciller dans une seule direction (polarisation rectiligne) ou peut tourner autour de l'axe de propagation de l'onde. On parle dans ce cas de polarisation circulaire ou elliptique. Le sens de la rotation, droite ou gauche, est également un paramètre clé qu'il faut mettre en regard de la biréfringence et de l'activité optique des milieux traversés.

La polarisation des ondes occupe un place importante dans de nombreux domaines scientifiques tels que l'optique, la séismologie, l'étude des ondes radiofréquences et micro-ondes. Les technologies concernée sont plus particulièrement les lasers, les télécommunications (fibrées ou non) et les radars.

Théorie

Explication du phénomène

La manifestation la plus simple de polarisation est celle d'une onde plane, qui est une bonne approximation de la plupart des ondes lumineuses. Comme toute onde électromagnétique qui se propage, elle est constituée d'un champ électrique et d'un champ magnétique tous deux perpendiculaires à la direction de propagation :

Onde lumineuse avec champ magnétique ${\vec {B}}$ et champ électrique ${\vec {E}}$ à angle droit l'un de l'autre (dans le cas d'une polarisation rectiligne).

On décide, par convention, d'ignorer le champ magnétique par la suite, car il peut être déterminé à partir du champ électrique. On considère donc uniquement le champ électrique ${\vec {E}}$ perpendiculaire à la direction de propagation.

Considérant les deux composantes vectorielles définissant l'orientation du champ électrique et conformément à la représentation ci-dessous, la figure décrite au cours du temps par le champ électrique en un point donné peut être alors :

• un segment de droite, cas de la polarisation rectiligne ;
• une ellipse, cas de la polarisation elliptique ;
• un cercle, cas de la polarisation circulaire.

Les trois figures en mouvement ci-dessous illustrent, pour chacun des trois cas, l'évolution temporelle du champ électrique ${\vec {E}}$ dans un plan d'onde fixé. Ces différentes formes définissent l'état de polarisation de l'onde : on dit que l'onde est polarisée rectilignement, elliptiquement ou circulairement.

Rectiligne	Elliptique	Circulaire

De plus, cette onde se propage dans l'espace, selon une direction précise, que l'on choisit verticale, perpendiculaire au plan d'onde horizontal, dans les figures ci-dessous (en trois dimensions) : ces courbes sont une représentation spatiale, instantanée, au temps $t_{0}$ fixé, des positions de la pointe de flèche du champ électrique dans tous les plans d'onde superposés verticalement le long de la propagation ; ces courbes sont construites en reportant à la distance verticale $d$ le vecteur champ qui existait dans le plan d'onde du bas à un instant passé $t=t_{0}-d/v$ ($v$ est la vitesse de propagation ; on tient compte ainsi de l'effet de la propagation) :

• La courbe de gauche représente la polarisation rectiligne ; c'est une sinusoïde tracée dans le plan vertical, passant par la diagonale du carré bleu, en bas.
• La courbe de droite représente la polarisation circulaire ; c'est une hélice qui s'enroule sur un cylindre vertical, dont la base est le cercle dessiné en perspective dans le carré du bas.
• La courbe du milieu représente la polarisation elliptique ; c'est une courbe ressemblant à une hélice, tracée sur un cylindre vertical, aplati, dont la base est l'ellipse dessinée dans le carré du bas.

Rectiligne	Elliptique	Circulaire

On peut se figurer la propagation en faisant glisser verticalement ces représentations spatiales instantanées : un instant $\Delta t$ plus tard, ces courbes doivent être remontées de la distance $\Delta d=v\Delta t$.

La symétrie des fonctions de l'espace et du temps, dans les équations de propagation, fait que les mêmes courbes peuvent aussi représenter mathématiquement les variations temporelles du champ électrique, dans un plan d'onde fixé, telles que nous les avons vues en mouvement dans la représentation animée ci-dessus (Il suffit alors de graduer en temps l'axe vertical).

Ce phénomène s'explique grâce à l'équation de propagation de l'onde lumineuse. En décomposant le champ électrique en ses deux composantes orthogonales (en bleu et rouge sur les schémas précédents), on s'aperçoit qu'elles ont toutes deux une évolution sinusoïdale. Lorsque les deux composantes oscillent en même temps, on obtient une polarisation rectiligne. Si elles présentent un déphasage (c'est-à-dire que l'une est en retard par rapport à l'autre), alors on obtient une polarisation elliptique.

Dans le cas particulier où ce déphasage vaut 90° et que les deux composantes ont même amplitude, la polarisation est circulaire. On distingue alors les cas de polarisation circulaire gauche et circulaire droite selon le sens de l'enroulement autour du cylindre.

Cette décomposition en deux composantes orthogonales est arbitraire. Il est aussi possible, par exemple, de décomposer en deux polarisations circulaires tournant en sens contraires.

La lumière incohérente

L'explication ci-dessus n'est valable strictement que pour une onde monochromatique, et plus particulièrement une lumière cohérente. Dans les autres cas, les effets sont un peu différents.

Par exemple, dans la lumière d'une ampoule à filament, on observe que la lumière est polarisée aléatoirement : elle ne correspond à aucun des trois cas précédents. Cela s'explique par le fait que cette lumière est composée de trains d'ondes, courtes impulsions lumineuses ayant chacune une amplitude, une fréquence, et une polarisation aléatoires. Ainsi, ce que nous observons est une moyenne de tous ces trains d'ondes qui nous apparaît non polarisée.

Toutefois, la lumière incohérente peut aussi présenter, en partie, une polarisation elliptique, circulaire, ou rectiligne. Pour déterminer alors quelle est la polarisation d'une lumière, on utilise des polariseurs et des lames à retard.

Représentation des états de polarisation

Il peut être nécessaire de représenter mathématiquement un état de polarisation de lumière, par exemple, afin de suivre son évolution à travers un système optique. On peut notamment utiliser :

• le formalisme de Jones, particulièrement adapté à la représentation d'états complètement polarisés ;
• les paramètres de Stokes, associés aux matrices de Mueller, qui permettent de décrire également la lumière partiellement polarisée.

Aspect corpusculaire

Toutes les explications ci-dessus sont données dans le cadre de l'optique physique. Cependant, la polarisation peut également être expliquée en utilisant l'aspect corpusculaire de la lumière.

La lumière est composée de photons possédant un spin de 1. La physique quantique nous enseigne donc que pour un photon, la projection sur un axe de son spin peut uniquement prendre les valeurs -1, 0 ou +1. Cependant, la valeur 0 est interdite par la théorie quantique des champs car la masse du photon est nulle. Les deux états propres correspondent donc soit à la valeur propre +1 (polarisation circulaire droite) ou à la valeur propre -1 (polarisation circulaire gauche). Conformément à la physique quantique, l'état de polarisation du photon est une combinaison linéaire de ces 2 états propres, ce qui permet de définir les polarisations rectilignes et elliptiques.

Sur WP anglais

Théorie

Hypothèses de départ

La plupart des sources de lumière sont incohérentes et dépolarisées (ou partiellement polarisées). Ces sources émettent un mélange d'ondes dont les propriétés spatiales et temporelles (telles que la phase, la longueur d'onde et la polarisation) sont aléatoires. Ces sources étant difficile à étudier, on simplifie dès le départ le problème.

Onde plane

Pour bien comprendre les ondes magnétiques et la polarisation, le moyen le plus simple est de considérer des ondes planes et cohérentes. Ces ondes sont sinusoïdales et peuvent être décrites par un vecteur d'onde, un fréquence, une phase et un état de polarisation uniques.

Le formalisme décrivant la polarisation s'appuie sur le modèle de l'onde plane cohérente. En optique, caractériser un système avec une telle onde permet de déduire ensuite le comportement du système avec des ondes moins simples. En effet, le théorème de superposition permet de décomposer n'importe quelle onde complexe en une somme d'ondes élémentaires. Cette décomposition est désignée par le terme de spectre angulaire. Ainsi, une onde réelle sera modélisée par une somme d'ondes planes décorrélées dont la phase et la fréquences seront réparties aléatoirement; même en travaillant avec des ondes très simples, on peut décrire in fine des ondes beaucoup plus compliquées.

Ondes transverses électrique (TE)

Une onde électromagnétique se propageant dans l'espace libre (ou tout autre milieu homogène, isotrope et transparent) peut-être qualifiée d'onde transverse. Cela signifie que ses vecteurs E de champ électrique et H de champ magnétique sont dans un plan orthogonal à la direction de propagation. De plus, les champs E et H sont orthogonaux entre eux. En choisissant une telle onde monochromatique se propageant selon l'axe z, on oblige E et H à être dans le plan défini par x et y. Pour décrire la phase, il est de plus d'usage d'utiliser une notation en nombres complexes. Les vrais champs E et H correspondent alors aux parties réelles de ces notations. En notant de plus t le temps, les ondes sont décrites par:

${\vec {E}}(z,t)={\begin{bmatrix}e_{x}\\e_{y}\\0\end{bmatrix}}\;e^{i(kz-\omega t)}$

and

${\vec {H}}(z,t)={\begin{bmatrix}h_{x}\\h_{y}\\0\end{bmatrix}}\;e^{i(kz-\omega t)}$

avec k la norme du vecteur d'onde et ω sa période. Cette expression rend compte à la fois de la dépendance temporelle et spatiale de l'onde.

De plus, E et H sont toujours orthogonaux, donc leur produit scalaire est nul.

${\vec {E}}({\vec {r}},t)\cdot {\vec {H}}({\vec {r}},t)=0$

Sachant qu'ils n'ont que des composantes selon x et y, l'équation précédente se résume à:

$e_{x}h_{x}+e_{y}h_{y}=0$

De plus, pour un milieu d'impédance η, e et h sont reliés par:

$h_{y}=e_{x}/\eta$

and

$h_{x}=-e_{y}/\eta$

Le formalisme de Jones permet de définir e_x et e_y (ce sont ses composantes). En général, le vecteur de Jones est complété par l'amplitude et la phase de l'onde.

$I=(|e_{x}|^{2}+|e_{y}|^{2})\,{\frac {1}{2\eta }}$

however the wave's state of polarization is only dependent on the (complex) ratio of e_y to e_x. So let us just consider waves whose |e_x|² + |e_y|² = 1; this happens to correspond to an intensity of about .00133 watts per square meter in free space (where $\eta =$ $\eta _{0}$). And since the absolute phase of a wave is unimportant in discussing its polarization state, let us stipulate that the phase of e_x is zero, in other words e_x is a real number while e_y may be complex. Under these restrictions, e_x and e_y can be represented as follows:

$e_{x}={\sqrt {\frac {1+Q}{2}}}$

$e_{y}={\sqrt {\frac {1-Q}{2}}}\,e^{i\phi }$

where the polarization state is now totally parameterized by the value of Q (such that -1 < Q < 1) and the relative phase $\phi$. By convention when one speaks of a wave's "polarization," if not otherwise specified, reference is being made to the polarization of the electric field. The polarization of the magnetic field always follows that of the electric field but with a 90 degree rotation, as detailed above.

Other types of polarization

In addition to transverse waves, there are many wave motions where the oscillation is not limited to directions perpendicular to the direction of propagation. These cases are beyond the scope of the current article which concentrates on transverse waves (such as most electromagnetic waves in bulk media), however one should be aware of cases where the polarization of a coherent wave cannot be described simply using a Jones vector, as we have just done.

Just considering electromagnetic waves, we note that the preceding discussion strictly applies to plane waves in a homogeneous isotropic non-attenuating medium, whereas in an anisotropic medium (such as birefringent crystals as discussed below) the electric or magnetic field may have longitudinal as well as transverse components. In those cases the electric displacement D and magnetic flux density B still obey the above geometry but due to anisotropy in the electric susceptibility (or in the magnetic permeability), now given by a tensor, the direction of E (or H) may differ from that of D (or B). Even in isotropic media, so-called inhomogeneous waves can be launched into a medium whose refractive index has a significant imaginary part (or "extinction coefficient") such as metals; these fields are also not strictly transverse. Surface waves or waves propagating in a waveguide (such as an optical fiber) are generally not transverse waves, but might be described as an electric or magnetic transverse mode, or a hybrid mode.

Even in free space, longitudinal field components can be generated in focal regions, where the plane wave approximation breaks down. An extreme example is radially or tangentially polarized light, at the focus of which the electric or magnetic field respectively is entirely longitudinal (along the direction of propagation).

For longitudinal waves such as sound waves in fluids, the direction of oscillation is by definition along the direction of travel, so the issue of polarization is not normally even mentioned. On the other hand, sound waves in a bulk solid can be transverse as well as longitudinal, for a total of three polarization components. In this case, the transverse polarization is associated with the direction of the shear stress and displacement in directions perpendicular to the propagation direction, while the longitudinal polarization describes compression of the solid and vibration along the direction of propagation. The differential propagation of transverse and longitudinal polarizations is important in seismology.

Polarization state

Over each cycle of a sinusoidal wave, the electric field vector (as well as the magnetic field) traces out an ellipse; note that a line and circle are special cases of ellipses. The shape and orientation of this ellipse (or line) defines the polarization state. The following figures show some examples of the evolution of the electric field vector (black), with time (the vertical axes), at a particular point in space, along with its x (red) and y (blue) components; at the base is the path traced by the vector in the transverse plane.

Linear polarization diagram

Linear

Circular polarization diagram

Circular

Elliptical polarization diagram

Elliptical

In the leftmost figure above, the electric field's x and y components (according to the axes we have established) are exactly in phase. The net result is polarization along a particular direction (depending on the relative amplitudes of the two components) in the x-y plane over each cycle. Since the vector traces out a single line in the plane, this special case is called linear polarization. Most polarizing filters produce linear polarization from unpolarized light.

In the middle figure, the x and y components still have the same amplitude but now are exactly ninety degrees out of phase. In this special case the electric vector traces out a circle in the plane, and is thus referred to as circular polarization. Depending on whether the phase difference is + or −90 degrees, it may be qualified as right-hand circular polarization or left-hand circular polarization, depending on one's convention.

The more general case with the two components out of phase by a different amount, or 90 degrees out of phase but with different amplitudes is called elliptical polarization because the electric vector traces out an ellipse (the polarization ellipse). This is shown in the above figure on the right. Again, the same ellipse shape can be produced either by a clockwise or counterclockwise rotation of the field, corresponding to distinct polarization states.

Animation of a circularly polarized wave as a sum of two components

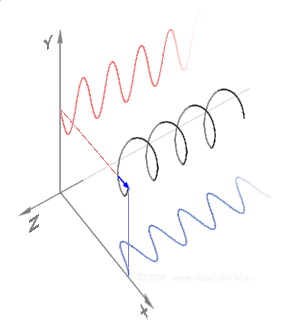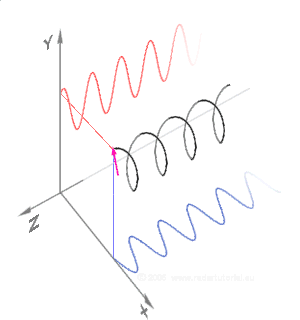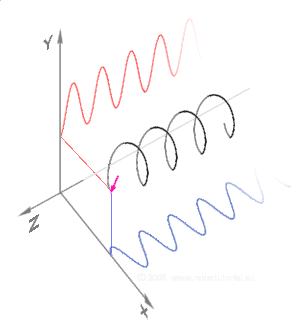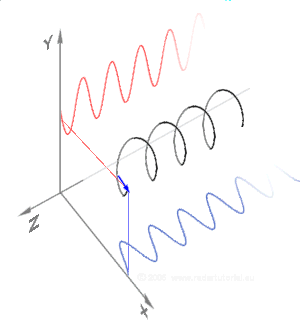
Of course the orientation of the x and y axes in such a picture is arbitrary, and any state of polarization can be represented regardless. One would typically chose axes to suit a particular problem such as x being in the plane of incidence. Moreover, one can use as basis functions any pair of orthogonal polarization states. Beyond the linear polarizations we have used here, the most useful choice is right and left circularly polarized states. The Cartesian polarization decomposition is natural when dealing with reflection from surfaces, birefringent materials, or synchrotron radiation. The circularly polarized modes are a more useful basis for the study of light propagation in stereoisomers.

Parameterization

For ease of visualization, polarization states are often specified in terms of the polarization ellipse, specifically its orientation and elongation. A common parameterization uses the orientation angle, ψ, the angle between the major semi-axis of the ellipse and the x-axis (also known as tilt angle or azimuth angle^{[réf. nécessaire]}) and the ellipticity, ε, the major-to-minor-axis ratio (also known as the axial ratio). An ellipticity of zero or infinity corresponds to linear polarization and an ellipticity of 1 corresponds to circular polarization. The ellipticity angle, χ = arccot ε= arctan 1/ε, is also commonly used. An example is shown in the diagram to the right. An alternative to the ellipticity or ellipticity angle is the eccentricity; however, unlike the azimuth angle and ellipticity angle, the latter has no obvious geometrical interpretation in terms of the Poincaré sphere (see below).

Full information on a completely polarized state is also provided by the amplitude and phase of oscillations in two components of the electric field vector in the plane of polarization. This representation was used above to show how different states of polarization are possible. The amplitude and phase information can be conveniently represented as a two-dimensional complex vector (the Jones vector):

$\mathbf {e} ={\begin{bmatrix}a_{1}e^{i\theta _{1}}\\a_{2}e^{i\theta _{2}}\end{bmatrix}}.$

Here $a_{1}$ and $a_{2}$ denote the amplitude of the wave in the two components of the electric field vector, while $\theta _{1}$ and $\theta _{2}$ represent the phases. The product of a Jones vector with a complex number of unit modulus gives a different Jones vector representing the same ellipse, and thus the same state of polarization. The physical electric field, as the real part of the Jones vector, would be altered but the polarization state itself is independent of absolute phase. The basis vectors used to represent the Jones vector need not represent linear polarization states (i.e. be real). In general any two orthogonal states can be used, where an orthogonal vector pair is formally defined as one having a zero inner product. A common choice is left and right circular polarizations, for example to model the different propagation of waves in two such components in circularly birefringent media (see below) or signal paths of coherent detectors sensitive to circular polarization.

Regardless of whether polarization ellipses are represented using geometric parameters or Jones vectors, implicit in the parameterization is the orientation of the coordinate frame. This permits a degree of freedom, namely rotation about the propagation direction. When considering light that is propagating parallel to the surface of the Earth, the terms "horizontal" and "vertical" polarization are often used, with the former being associated with the first component of the Jones vector, or zero azimuth angle. On the other hand, in astronomy the equatorial coordinate system is generally used instead, with the zero azimuth (or position angle, as it is more commonly called in astronomy to avoid confusion with the horizontal coordinate system) corresponding to due north.

s and p designations

Another coordinate system frequently used relates to the plane made by the propagation direction and a vector perpendicular to the plane of a reflecting surface. This is known as the plane of incidence. The component of the electric field parallel to this plane is termed p-like (parallel) and the component perpendicular to this plane is termed s-like (from senkrecht, German for perpendicular). Polarized light with its electric field along the plane of incidence is thus denoted p-polarized, while light whose electric field is normal to the plane of incidence is called s-polarized. p polarization is commonly referred to as transverse-magnetic (TM), and has also been termed pi-polarized or tangential plane polarized. s polarized light is also called transverse-electric (TE), as well as sigma-polarized or sagittal plane polarized.

Unpolarized light

Most common sources of visible light, including thermal (black body) radiation and fluorescence (but not lasers), produce light described as "incoherent". Radiation is produced independently by a large number of atoms or molecules whose emissions are uncorrelated and generally of random polarizations. In this case the light is said to be unpolarized. This term is somewhat inexact, since at any instant of time at one location there is a definite direction to the electric and magnetic fields, however it implies that the polarization changes so quickly in time that it will not be measured or relevant to the outcome of an experiment. A so-called depolarizer acts on a polarized beam to create one which is actually fully polarized at every point, but in which the polarization varies so rapidly across the beam that it may be ignored in the intended applications.

Light is said to be partially polarized when there is more power in one polarization mode than another. At any particular wavelength, partially polarized light can be statistically described as the superposition of a completely unpolarized component, and a completely polarized one. One may then describe the light in terms of the degree of polarization, and the parameters of the polarized component. Stokes parameters are the most common way of specifying such states of partial polarization.

Polarization in wave propagation

In a vacuum, the components of the electric field propagate at the speed of light, so that the phase of the wave varies in space and time while the polarization state does not. That is, the electric field vector e of a plane wave in the +z direction follows:

$\mathbf {e} (z+\Delta z,t+\Delta t)=\mathbf {e} (z,t)e^{ik(c\Delta t-\Delta z)},$

where k is the wavenumber. As noted above, the instantaneous electric field is the real part of the product of the Jones vector times the phase factor $e^{-i\omega t}$. When an electromagnetic wave interacts with matter, its propagation is altered according to the material's (complex) index of refraction. When the real or imaginary part of that refractive index is dependent on the polarization state of a wave, properties known as birefringence and polarization dichroism (or diattenuation) respectively, then the polarization state of a wave will generally be altered.

In such media, an electromagnetic wave with any given state of polarization may be decomposed into two orthogonally polarized components that encounter different propagation constants. The effect of propagation over a given path on those two components is most easily characterized in the form of a complex 2×2 transformation matrix J known as a Jones matrix:

$\mathbf {e'} =\mathbf {J} \mathbf {e} .$

The Jones matrix due to passage through a transparent material is dependent on the propagation distance as well as the birefringence. The birefringence (as well as the average refractive index) will generally be dispersive, that is, it will vary as a function of optical frequency (wavelength). In the case of non-birefringent materials, however, the 2×2 Jones matrix is the identity matrix (multiplied by a scalar phase factor and attenuation factor), implying no change in polarization during propagation.

For propagation effects in two orthogonal modes, the Jones matrix can be written as

$\mathbf {J} =\mathbf {T} {\begin{bmatrix}g_{1}&0\\0&g_{2}\end{bmatrix}}\mathbf {T} ^{-1},$

where g₁ and g₂ are complex numbers describing the phase delay and possibly the amplitude attenuation due to propagation in each of the two polarization eigenmodes. T is a unitary matrix representing a change of basis from these propagation modes to the linear system used for the Jones vectors; in the case of linear birefringence or diattenuation the modes are themselves linear polarization states so T and T⁻¹ can be omitted if the coordinate axes have been chosen appropriately. In media termed birefringent, in which the amplitudes are unchanged but a differential phase delay occurs, the Jones matrix is a unitary matrix: |g₁| = |g₂| = 1. Media termed diattenuating (or dichroic in the sense of polarization), in which only the amplitudes of the two polarizations are affected differentially, may be described using a Hermitian matrix (generally multiplied by a common phase factor). In fact, since any matrix may be written as the product of unitary and positive Hermitian matrices, light propagation through any sequence of polarization-dependent optical components can be written as the product of these two basic types of transformations.

Color pattern of a plastic box possessing stress induced birefringence when placed in between two crossed polarizers.

In birefringent media there is no attenuation but two modes accrue a differential phase delay. Well known manifestations of linear birefringence (that is, in which the basis polarizations are orthogonal linear polarizations) appear in optical wave plates/retarders and many crystals. If linearly polarized light passes through a birefringent material, its state of polarization will generally change unless its polarization direction is identical to one of those basis polarizations. Since the phase shift, and thus the change in polarization state, is usually wavelength dependent, such objects viewed under white light in between two polarizers may give rise to colorful effects, as seen in the accompanying photograph.

Circular birefringence is also termed optical activity especially in chiral fluids, or Faraday rotation when due to the presence of a magnetic field along the direction of propagation. When linearly polarized light is passed through such an object, it will exit still linearly polarized but with the axis of polarization rotated. A combination of linear and circular birefringence will have as basis polarizations two orthogonal elliptical polarizations; the term "elliptical birefringence" however is rarely used.

Birefringence diagram

Paths taken by vectors in the Poincaré sphere under birefringence. The propagation modes (rotation axes) are shown with red, blue, and yellow lines, the initial vectors by thick black lines, and the paths they take by colored ellipses (which represent circles in three dimensions).

One can visualize the case of linear birefringence (with two orthogonal linear propagation modes) with an incoming wave linearly polarized at a 45° angle to those modes. As a differential phase starts to accrue, the polarization becomes elliptical, eventually changing to purely circular polarization (90° phase difference), then to elliptical and eventually linear polarization (180° phase) perpendicular to the original polarization, then through circular again (270° phase), then elliptical with the original azimuth angle, and finally back to the original linearly polarized state (360° phase) where the cycle begins anew. In general the situation is more complicated and can be characterized as a rotation in the Poincaré sphere about the axis defined by the propagation modes. Examples for linear (blue), circular (red), and elliptical (yellow) birefringence are shown in the figure on the left. The total intensity and degree of polarization are unaffected. If the path length in the birefringent medium is sufficient, the two polarization components of a collimated beam (or ray) can exit the material with a positional offset, even though their final propagation directions will be the same (assuming the entrance face and exit face are parallel). This is commonly viewed using calcite crystals, which present the viewer with two slightly offset images, in opposite polarizations, of an object behind the crystal. It was this effect that provided the first discovery of polarization, by Erasmus Bartholinus in 1669.

Media in which the amplitude of one polarization mode is preferentially reduced are called dichroic or diattenuating. In terms of the Poincaré sphere, an input polarization state is "dragged" in the direction of the preferred mode. Devices that block nearly all of the radiation in one mode are known as polarizing filters or simply "polarizers". This corresponds to g₂=0 in the above representation of the Jones matrix. The output is a specific polarization state but with an amplitude equal to the input wave's original amplitude in that polarization mode. Power in the other polarization mode is absorbed (or diverted). Thus if unpolarized light is passed through an ideal polarizer (where g₁=1 and g₂=0) exactly half of its initial power is retained. Practical polarizers, especially inexpensive sheet polarizers, have additional loss so that g₁ < 1. However in many instances the more relevant figure of merit is the polarizer's degree of polarization or extinction ratio which involves a comparison of g₁ to g₂. Since Jone's vectors refer to waves' amplitudes (rather than intensity), when illuminated by unpolarized light the remaining power in the unwanted polarization will be (g₂/g₁)² of the power in the intended polarization.

Polarization in specular reflection

In addition to birefringence and dichroism in extended media, polarization effects describable using Jones matrices can also occur at (reflective) interface between two materials of different refractive index. These effects are treated by the Fresnel equations. Part of the wave is transmitted and part is reflected; for a given material those proportions (and also the phase of reflection) are dependent on the angle of incidence and are different for the s and p polarizations. Therefore the polarization state of reflected light (even if initially unpolarized) is generally changed.

A stack of plates at Brewster's angle to a beam reflects off a fraction of the s-polarized light at each surface, leaving (after many such plates) a mainly p-polarized beam.

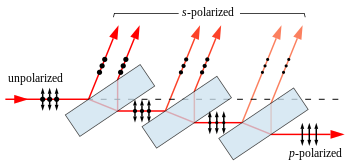
Any light striking a surface at a special angle of incidence known as Brewster's angle, where the reflection coefficient for p polarization is zero, will be reflected with only the s-polarization remaining. This principle is employed in the so-called "pile of plates polarizer" (see figure) in which part of the s polarization is removed by reflection at each Brewster angle surface, leaving only the p polarization after transmission through many such surfaces. The generally smaller reflection coefficient of the p polarization is also the basis of polarized sunglasses; by blocking the s (horizontal) polarization, most of the glare due to reflection from a wet street, for instance, is removed.

In the important special case of reflection at normal incidence (not involving anisotropic materials) there is no particular s or p polarization. Both the x and y polarization components are reflected identically, and therefore the polarization of the reflected wave is identical to that of the incident wave. However in the case of circular (or elliptical) polarization, the handedness of the polarization state is thereby reversed, since by convention this is specified relative to the direction of propagation. The circular rotation of the electric field around the x-y axes called "right-handed" for a wave in the +z direction is "left-handed" for a wave in the -z direction. But in the general case of reflection at a nonzero angle of incidence, no such generalization can be made. For instance, right-circularly polarized light reflected from a dielectric surface at a grazing angle, will still be right-handed (but elliptically) polarized. Linear polarized light reflected from a metal at non-normal incidence will generally become elliptically polarized. These cases are handled using Jones vectors acted upon by the different Fresnel coefficients for the s and p polarization components.

Optical scattering

The transmission of plane waves through a homogeneous medium are fully described in terms of Jones vectors and 2×2 Jones matrices. However in practice there are cases in which all of the light cannot be viewed in such a simple manner due to spatial inhomogeneities or the presence of mutually incoherent waves. So-called depolarization, for instance, cannot be described using Jones matrices. For these cases it is usual instead to use a 4×4 matrix that acts upon the Stokes 4-vector. Such matrices were first used by Paul Soleillet in 1929, although they have come to be known as Mueller matrices. While every Jones matrix has a Mueller matrix, the reverse is not true. Mueller matrices are then used to describe the observed polarization effects of the scattering of waves from complex surfaces or ensembles of particles, as shall now be presented.

Parameterization of incoherent or partially polarized radiation

Modèle:Principal Les vecteurs de Jones décrivent parfaitement l'état de polarisation et la phase d'une unique onde monochromatique. Cependant, dès lors qu'on s'intéresse à des mélanges d'ondes ayant différentes polarisations (ou différentes fréquences), le paramètre de Jones ne peut plus être utilisé.

The Jones vector perfectly describes the state of polarization and phase of a single monochromatic wave, representing a pure state of polarization as described above. However any mixture of waves of different polarizations (or even of different frequencies) do not correspond to a Jones vector. In so-called partially polarized radiation the fields are stochastic, and the variations and correlations between components of the electric field can only be described statistically. One such representation is the coherency matrix:

$\mathbf {\Psi } =\left\langle \mathbf {e} \mathbf {e} ^{\dagger }\right\rangle \,$

$=\left\langle {\begin{bmatrix}e_{1}e_{1}^{*}&e_{1}e_{2}^{*}\\e_{2}e_{1}^{*}&e_{2}e_{2}^{*}\end{bmatrix}}\right\rangle$

$=\left\langle {\begin{bmatrix}a_{1}^{2}&a_{1}a_{2}e^{i(\theta _{1}-\theta _{2})}\\a_{1}a_{2}e^{-i(\theta _{1}-\theta _{2})}&a_{2}^{2}\end{bmatrix}}\right\rangle$

where angular brackets denote averaging over many wave cycles. Several variants of the coherency matrix have been proposed: the Wiener coherency matrix and the spectral coherency matrix of Richard Barakat measure the coherence of a spectral decomposition of the signal, while the Wolf coherency matrix averages over all time/frequencies.

The coherency matrix contains all second order statistical information about the polarization. This matrix can be decomposed into the sum of two idempotent matrices, corresponding to the eigenvectors of the coherency matrix, each representing a polarization state that is orthogonal to the other. An alternative decomposition is into completely polarized (zero determinant) and unpolarized (scaled identity matrix) components. In either case, the operation of summing the components corresponds to the incoherent superposition of waves from the two components. The latter case gives rise to the concept of the "degree of polarization"; i.e., the fraction of the total intensity contributed by the completely polarized component.

The coherency matrix is not easy to visualize, and it is therefore common to describe incoherent or partially polarized radiation in terms of its total intensity (I), (fractional) degree of polarization (p), and the shape parameters of the polarization ellipse. An alternative and mathematically convenient description is given by the Stokes parameters, introduced by George Gabriel Stokes in 1852. The relationship of the Stokes parameters to intensity and polarization ellipse parameters is shown in the equations and figure below.

Poincaré sphere diagram

$S_{0}=I\,$

$S_{1}=Ip\cos 2\psi \cos 2\chi \,$

$S_{2}=Ip\sin 2\psi \cos 2\chi \,$

$S_{3}=Ip\sin 2\chi \,$

Here Ip, 2ψ and 2χ are the spherical coordinates of the polarization state in the three-dimensional space of the last three Stokes parameters. Note the factors of two before ψ and χ corresponding respectively to the facts that any polarization ellipse is indistinguishable from one rotated by 180°, or one with the semi-axis lengths swapped accompanied by a 90° rotation. The Stokes parameters are sometimes denoted I, Q, U and V.

The Stokes parameters contain all of the information of the coherency matrix, and are related to it linearly by means of the identity matrix plus the three Pauli matrices:

$\mathbf {\Psi } ={\frac {1}{2}}\sum _{j=0}^{3}S_{j}\mathbf {\sigma } _{j},{\text{ where}}$

${\begin{matrix}\mathbf {\sigma } _{0}&=&{\begin{bmatrix}1&0\\0&1\end{bmatrix}}&\mathbf {\sigma } _{1}&=&{\begin{bmatrix}1&0\\0&-1\end{bmatrix}}\\\\\mathbf {\sigma } _{2}&=&{\begin{bmatrix}0&1\\1&0\end{bmatrix}}&\mathbf {\sigma } _{3}&=&{\begin{bmatrix}0&-i\\i&0\end{bmatrix}}\end{matrix}}$

Mathematically, the factor of two relating physical angles to their counterparts in Stokes space derives from the use of second-order moments and correlations, and incorporates the loss of information due to absolute phase invariance.

The figure above makes use of a convenient representation of the last three Stokes parameters as components in a three-dimensional vector space. This space is closely related to the Poincaré sphere, which is the spherical surface occupied by completely polarized states in the space of the vector

$\mathbf {u} ={\frac {1}{S_{0}}}{\begin{bmatrix}S_{1}\\S_{2}\\S_{3}\end{bmatrix}}.$

All four Stokes parameters can also be combined into the four-dimensional Stokes vector, which can be interpreted as four-vectors of Minkowski space. In this case, all physically realizable polarization states correspond to time-like, future-directed vectors.

Measurement techniques involving polarization

Some optical measurement techniques are based on polarization. In many other optical techniques polarization is crucial or at least must be taken into account and controlled; such examples are too numerous to mention.

Measurement of stress

Stress in plastic glasses

In engineering, the phenomenon of stress induced birefringence allows for stresses in transparent materials to be readily observed. As noted above and seen in the accompanying photograph, the chromaticity of birefringence typically creates colored patterns when viewed in between two polarizers. As external forces are applied, internal stress induced in the material is thereby observed. Additionally, birefringence is frequently observed due to stresses "frozen in" at the time of manufacture. This is famously observed in cellophane tape whose birefringence is due to the stretching of the material during the manufacturing process.

Ellipsometry

Ellipsometry is a powerful technique for the measurement of the optical properties of a uniform surface. It involves measuring the polarization state of light following specular reflection from such a surface. This is typically done as a function of incidence angle or wavelength (or both). Since ellipsometry relies on reflection, it is not required for the sample to be transparent to light or for its back side to be accessible.

Ellipsometry can be used to model the (complex) refractive index of a surface of a bulk material. It is also very useful in determining parameters of one or more thin film layers deposited on a substrate. Due to their reflection properties, not only are the predicted magnitude of the p and s polarization components, but their relative phase shifts upon reflection, compared to measurements using an ellipsometer. A normal ellipsometer does not measure the actual reflection coefficient (which requires careful photometric calibration of the illuminating beam) but the ratio of the p and s reflections, as well as change of polarization ellipticity (hence the name) induced upon reflection by the surface being studied. In addition to use in science and research, ellipsometers are used in situ to control production processes for instance.

Geology

Photomicrograph of a volcanic sand grain; upper picture is plane-polarized light, bottom picture is cross-polarized light, scale box at left-center is 0.25 millimeter.

The property of (linear) birefringence is widespread in crystalline minerals, and indeed was pivotal in the initial discovery of polarization. In mineralogy, this property is frequently exploited using polarization microscopes, for the purpose of identifying minerals. See optical mineralogy for more details.

Sound waves in solid materials exhibit polarization. Differential propagation of the three polarizations through the earth is a crucial in the field of seismology. Horizontally and vertically polarized seismic waves (shear waves)are termed SH and SV, while waves with longitudinal polarization (compressional waves) are termed P-waves.

Chemistry

We have seen (above) that the birefringence of a type of crystal is useful in identifying it, and thus detection of linear birefringence is especially useful in geology and mineralogy. Linearly polarized light generally has its polarization state altered upon transmission through such a crystal, making it stand out when viewed in between two crossed polarizers, as seen in the photograph, above. Likewise, in chemistry, rotation of polarization axes in a liquid solution can be a useful measurement. In a liquid, linear birefringence is impossible, however there may be circular birefringence when a chiral molecule is in solution. When the right and left handed enantiomers of such a molecule are present in equal numbers (a so-called racemic mixture) then their effects cancel out. However when there is only one (or a preponderance of one), as is more often the case for organic molecules, a net circular birefringence (or optical activity) is observed, revealing the magnitude of that imbalance (or the concentration of the molecule itself, when it can be assumed that only one enantiomer is present). This is measured using a polarimeter in which polarized light is passed through a tube of the liquid, at the end of which is another polarizer which is rotated in order to null the transmission of light through it.

Astronomy

In many areas of astronomy, the study of polarized electromagnetic radiation from outer space is of great importance. Although not usually a factor in the thermal radiation of stars, polarization is also present in radiation from coherent astronomical sources (e.g. hydroxyl or methanol masers), and incoherent sources such as the large radio lobes in active galaxies, and pulsar radio radiation (which may, it is speculated, sometimes be coherent), and is also imposed upon starlight by scattering from interstellar dust. Apart from providing information on sources of radiation and scattering, polarization also probes the interstellar magnetic field via Faraday rotation. The polarization of the cosmic microwave background is being used to study the physics of the very early universe. Synchrotron radiation is inherently polarised. It has been suggested that astronomical sources caused the chirality of biological molecules on Earth.

Angular momentum using circular polarization

It is well known that electromagnetic radiation carries a certain linear momentum in the direction of propagation. In addition, however, light carries a certain angular momentum if it is circularly polarized (or partially so). In comparison with lower frequencies such as microwaves, the amount of angular momentum in light, even of pure circular polarization, compared to the same wave's linear momentum (or radiation pressure) is very small and difficult to even measure. However it was utilized in a remarkable experiment to achieve an incredibly high rotation speed.

The University of St Andrews team caused a microscopic bead of calcium carbonate 4 micrometres in diameter to rotate at speeds of up to 600 million revolutions per minute. The bead was suspended by a laser beam in a location using the principle of optical tweezers. However that beam was also circularly polarized. The calcium carbonate (calcite) bead, being birefringent, caused light transmitted through it to slightly change its polarization into one that was not fully circularly polarized, and which therefore had less angular momentum. The difference in the angular momentum between the incident beam and light transmitted through the bead was imparted to the bead itself. Suspended in a near-vacuum and facing little friction, the rotation rate of the bead could be increased to rates as high as 10 million revolutions per second. This rotation rate corresponded to a centrifugal acceleration some one billion times that of gravity on the Earth surface, but which surprisingly did not lead to the bead's disintegration.

See also

Polaroid (polarizer) Depolarizer (optics) Radial polarisation Fluorescence anisotropy Rayleigh Sky Model Nicol prism Photon polarization Polarized light microscopy Kerr effect Pockels effect Polarization rotator Notes and references External links Polarized Light in Nature and Technology Polarized Light Digital Image Gallery: Microscopic images made using polarization effects Polarization by the University of Colorado Physics 2000: Animated explanation of polarization MathPages: The relationship between photon spin and polarization A virtual polarization microscope Polarization angle in satellite dishes. Using polarizers in photography Molecular Expressions: Science, Optics and You — Polarization of Light: Interactive Java tutorial Electromagnetic waves and circular dichroism: an animated tutorial HyperPhysics: Polarization concepts Tutorial on rotating polarization through waveplates (retarders) SPIE technical group on polarization A Java simulation on using polarizers Antenna Polarization Animations of Linear, Circular and Elliptical Polarizations on YouTube