Théorème de Borsuk-Ulam

Stanislaw Ulam conjecture le théorème, mais ne parvient pas à le démontrer dans le cas général.

En mathématiques, le théorème de Borsuk-Ulam est un résultat de topologie algébrique. Il indique que pour toute fonction f continue d'une sphère de dimension n, c'est-à-dire la frontière de la boule euclidienne de ℝⁿ⁺¹, dans un espace euclidien de dimension n, il existe deux points antipodaux, c'est-à-dire diamétralement opposés, ayant même image par f.

Il fait partie des « quelques grands théorèmes concernant la topologie des espaces de dimension finie. » Contrairement au théorème de Jordan, il est peu intuitif. Il indique par exemple qu'à tout instant, il existe deux points antipodaux de la Terre ayant exactement la même température et la même pression (on suppose que ces deux grandeurs évoluent de façon continue).

Son premier usage concerne la topologie algébrique ; il permet par exemple de démontrer le théorème du point fixe de Brouwer qui lui est analogue à certains égards. Il permet de démontrer des résultats au titre aussi amusant que leur démonstration est difficile, comme le théorème du sandwich au jambon ou encore le problème du partage d'un collier. À partir des années 1970, il devient un outil pour démontrer des résultats de dénombrement, liés à la théorie des graphes.

Ce théorème fut conjecturé par Stanislaw Ulam et prouvé par Karol Borsuk en 1933.

Énoncé

Théorème — Toute application continue de la sphère S^n–1 dans un espace euclidien de dimension n – 1 est telle qu'il existe deux points antipodaux ayant même image.

Démonstrations

Dimension un

En dimension un, la preuve est une conséquence directe d'un résultat analogue au théorème des valeurs intermédiaires. Soit f la fonction continue du cercle, de centre le vecteur nul, dans ℝ. On définit la fonction g du cercle dans ℝ, qui à x associe g(x) = f(x) – f(–x). Le théorème revient à montrer que g possède un zéro. On remarque que la fonction g est impaire, c'est-à-dire que g(–x) = –g(x).

Soit x₀ un point du cercle. Si g(x₀) est nul, le théorème est démontré. Dans le cas contraire, l'image de g est connexe car le cercle l'est. Cette image contient donc le segment d'extrémités g(x₀) et –g(x₀). Ce segment contient 0, qui possède donc un antécédent.

Sous cette forme, le théorème n'est guère étonnant. Un corollaire est un peu plus surprenant : si deux fermés du cercle ont pour union le cercle entier, l'un des deux fermés contient deux points antipodaux. En effet, soit A et B les deux ensembles non vides et fermés dont l'union est égale au cercle. On considère la fonction f qui, au point x du cercle, associe la distance de x à A. Le théorème assure l'existence de deux points x et –x ayant même image par f. Si cette image est 0, alors x et –x sont tous deux dans A car A est fermé, et le corollaire est démontré. Dans le cas contraire, ils sont tous deux dans B et le corollaire est à nouveau démontré.

Dimension deux

Une méthode classique en dimension 2 fait appel au groupe fondamental du cercle. On raisonne par l'absurde et l'on suppose qu'il existe une fonction f de la sphère S² dans ℝ² telle que tous les points antipodaux ont des images distinctes par f. On associe à f une certaine fonction continue g, de la sphère S² dans le cercle S¹. L'application g induit un morphisme g_✻ du groupe fondamental de S² dans celui de S¹. Comme S² possède un groupe fondamental trivial car la sphère est simplement connexe, les images des lacets par g_✻ devraient tous être homotopes à un point. On construit un lacet dont l'image ne l'est pas. Cette contradiction démontre le théorème.

Détails

On définit la fonction g sur la sphère unité S² par :

$\forall x\in S^{2}\quad g(x)={\frac {f(x)-f(-x)}{\|f(x)-f(-x)\|}}.$

Comme on suppose qu'il n'existe aucun couple de points antipodaux ayant la même image par f, la fonction g est bien définie. On considère le lacet α de S², qui à t associe le point de coordonnées (cos(2πt), sin(2πt), 0). Comme la fonction g est impaire, on dispose de l'égalité :

$(1)\quad \forall t\in [0,1/2]\quad g_{*}\alpha (t+1/2)=-g_{*}\alpha (t).$

Par ailleurs, il existe une fonction p continue de [0, 1] dans ℝ telle que le lacet g_✻α du cercle unité S¹ s'écrive :

$\forall t\in [0,1]\quad g_{*}\alpha (t)=(\cos(2\pi p(t)),\sin(2\pi p(t)))\quad {\text{avec }}p(0)=0.$

La propriété (1) permet de déduire :

$\forall t\in [0,1/2]\quad 2\left(p(t+1/2)-p(t)\right)\in \mathbb {Z} .$

La fonction qui à t associe p(t + 1/2) – p(t) est continue, définie sur un ensemble connexe et à valeurs dans un ensemble discret ; elle est donc constante. Cette constante est de la forme c/2 où c est un entier impair. On en déduit les égalités :

$p(1)=p(1/2)+c/2=(p(0)+c/2)+c/2=c.$

Le fait que c soit un entier impair montre que p(1) est un entier non nul et donc que g_✻α n'est pas homotope à un point. En fait, le lacet g_✻α fait c tours autour du cercle. Le morphisme g_✻ est un morphisme du groupe trivial dans un groupe isomorphe à ℤ et possède une image différente de l'élément neutre. Cette impossibilité termine le raisonnement par l'absurde.

Corollaires

Partage d'une sphère

Si trois fermés recouvrent une sphère, l'un au moins contient deux points antipodaux.

Le corollaire démontré pour le cercle se généralise. Cette fois-ci, la sphère est divisée en trois parties fermées comme illustré sur la figure de droite, la bleue, notée A, la rouge notée B et la verte C. Dans l'exemple, c'est la zone verte qui contient les points antipodaux. Une fois encore, le centre de la sphère est placé sur le vecteur nul, deux points antipodaux sont ainsi opposés.

On considère la fonction, qui à x, associe le couple f(x) = (d_A(x), d_B(x)) : la première composante indique la distance séparant x de A et la deuxième celle qui sépare x de B. La fonction f étant continue, le théorème de Borsuk-Ulam assure l'existence de deux points antipodaux ayant même image par f. Si cette image comporte une coordonnée nulle, les points x et –x sont, soit dans A, soit dans B, car A et B sont fermés. Dans le cas contraire, x et –x sont nécessairement tous deux dans C.

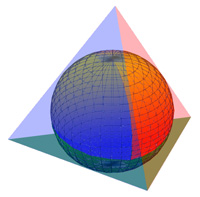
On peut se demander si 3 est bien le nombre maximal pour décomposer une sphère en fermés contenant nécessairement deux points antipodaux dans un même fermé. Pour s'en persuader, le plus simple est de placer la sphère dans un tétraèdre régulier circonscrit à la sphère, comme illustré sur la figure de gauche. On associe à chaque face du tétraèdre, un fermé de la sphère de la manière suivante. On considère un point p de la sphère et la demi-droite d'extrémité le centre de la sphère et passant par p. Si cette demi-droite rencontre une face du tétraèdre, le point p est élément du fermé associé à cette face (certains points de la sphère sont associés à deux faces si l'intersection est sur une arête). Aucun des quatre fermés ne contient de paire de points antipodaux.

Le raisonnement proposé ici se généralise pour une dimension quelconque.

Théorème du sandwich au jambon

Le théorème du sandwich au jambon annonce l'existence d'un plan qui coupe chacun des trois solides en deux parties de volumes égaux.

Le théorème du sandwich au jambon dans le cas où n est égal à 3 s'exprime de manière suivante. Soit trois parties mesurables et de mesure finie d'un espace euclidien de dimension trois. On les représente par le jambon, le fromage et le pain d'un sandwich. Il existe un plan affine qui coupe simultanément chacune des trois parties en deux sous-ensembles de volumes égaux. Plus généralement, le théorème implique :

Étant données n parties Lebesgue-mesurables et de mesures finies d'un espace euclidien de dimension n, il existe au moins un hyperplan affine divisant chaque partie en deux sous-ensembles de mesures égales.

Cette question est initialement posée par Hugo Steinhaus dans le cas de la dimension 3 et est aussitôt résolue en 1938 par Stefan Banach à l'aide du théorème de Borsuk-Ulam. La réponse à cette question d'apparence aussi ludique qu'anodine est la clé de questions très sérieuses. Luis Paris remarque que : « […] c’est avec ces mêmes techniques que les mathématiciens ont établi l’existence d’enzymes appelées topo-isomérases qui effectuent des manipulations topologiques sur l'ADN ».

Partage discret du collier

Exemple de partage, entre q = 2 voleurs, d'un collier de perles de t = 2 couleurs (3q = 6 vertes et 4q = 8 rouges) : t(q – 1) = 2 coupes suffisent.

Le problème du partage discret du collier est beaucoup plus délicat à démontrer, même si son apparence est des plus simples. On présente souvent ce problème ainsi : deux voleurs dérobent un collier composé de perles de t couleurs différentes, avec un nombre pair de perles de chaque couleur. Ces perles sont fixées sur une chaînette ouverte. Ne connaissant pas la valeur des différentes couleurs de perles, ils veulent se répartir autant de perles de chaque couleur. De plus, pour préserver les maillons d'or de la chaînette, ils souhaitent effectuer le moins de coupes possibles.

Si les perles de chacune des t couleurs sont contigües, il faut bien sûr au moins t coupes. Le théorème indique que, quelle que soit la configuration, ce nombre t de coupes est toujours suffisant.

Lorsque t est égal à 2, ce théorème se démontre de façon élémentaire : si le collier contient par exemple 2a perles vertes et 2b perles rouges et si, parmi les a + b premières à partir d'une extrémité, il y a strictement plus de a perles vertes (donc strictement moins de b rouges) alors, en translatant pas à pas cette « fenêtre » de taille a + b le long du collier, on aboutit, à l'autre extrémité, à la situation opposée, donc lors d'une étape intermédiaire, le partage est équitable.

Le théorème pour t quelconque a été démontré pour la première fois en 1985. La démonstration est considérablement simplifiée par Alon et West 1986, en utilisant le théorème de Borsuk-Ulam.

Le cas où le nombre de voleurs n'est pas 2 mais devient une valeur q quelconque (avec, dans chacune des t couleurs, un nombre de perles multiple de q) est traité l'année suivante par Alon, en utilisant un théorème qui généralise à la fois celui de Borsuk-Ulam et celui de Tverberg : il suffit de t(q – 1) coupes.

À la différence des exemples précédents, le théorème de Borsuk-Ulam quitte ici son champ d'application naturel — la topologie algébrique — pour devenir la cheville ouvrière d'un résultat de dénombrement.

Notes et références

Bibliographie

• (en) Noga Alon et Douglas B. West, « The Borsuk-Ulam theorem and bisection of necklaces », Proc. Amer. Math. Soc., vol. 98,‎ 1986, p. 623-628
• (en) Glen E. Bredon, Topology and geometry, Springer, coll. « GTM » (n^o 139), 1993, 557 p. (ISBN 978-0-387-97926-7, lire en ligne)
• (en) Allen Hatcher, Algebraic Topology, New York, CUP, 2001, 544 p. (ISBN 978-0-521-79540-1, lire en ligne)
• (en) Jiří Matoušek, Using the Borsuk-Ulam Theorem : Lectures on Topological Methods in Combinatorics and Geometry, Springer, 2003, 196 p. (ISBN 978-3-540-00362-5, lire en ligne)
• F. Meunier, Pleins étiquetages et configurations équilibrées : aspects topologiques de l'Optimisation Combinatoire, thèse de l'université Joseph Fourier, 2006 (lire en ligne), chap. 5

Voir aussi

Articles connexes

• Degré d'une application
• Lemme de Sperner
• Lemme de Tucker (en)
• Théorème de Kakutani-Yamabe-Yujobô (de)

Liens externes

• (en) Borsuk-Ulam theorem and a proof, sur PlanetMath
• (en) S. Arora, The Borsuk-Ulam theorem, un cours de l'université de Princeton
• (en) [vidéo] 3Blue1Brown, Sneaky Topology : The Borsuk-Ulam theorem and stolen necklaces sur YouTube : preuve animée du théorème de Borsuk-Ulam et de son application au problème du partage de collier.