Problème de Hadwiger-Nelson

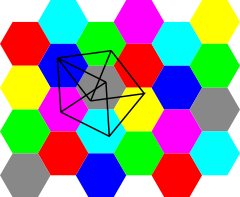
Un article de Wikipédia, l'encyclopédie libre.
Coloration du plan en sept couleurs, et dessin du graphe de Moser, exhibant des bornes supérieures et inférieures pour le problème de Hadwiger–Nelson.

En théorie géométrique des graphes (en), le problème de Hadwiger-Nelson, posé par Hugo Hadwiger et Edward Nelson vers 1950, consiste à déterminer le nombre minimum de couleurs nécessaires pour colorier le plan de telle sorte que deux points séparés d'une unité soient toujours de couleurs distinctes. La réponse est inconnue, mais est l'un des trois entiers 5, 6 ou 7 ; la valeur exacte pourrait d'ailleurs dépendre de l'axiome du choix.

Historique[modifier | modifier le code]

Le problème fut énoncé par Edward Nelson en 1950[1], et publié par Martin Gardner en 1960[2]. Cependant, Hugo Hadwiger avait publié auparavant un résultat apparenté, montrant que pour tout revêtement du plan par cinq ensembles fermés congruents, il existe deux points séparés d'une unité et situés dans le même ensemble[3] ; il mentionna le problème sous sa forme exacte dans une publication ultérieure[4]. En 2008, Alexander Soifer a publié une étude approfondie du problème et de son histoire[5].

Énoncé du problème[modifier | modifier le code]

En termes de théorie des graphes, la question peut s'énoncer ainsi : soit G le graphe distance-unité du plan, c'est-à-dire le graphe dont les sommets sont tous les points du plan (euclidien) et dont les arêtes relient deux points si et seulement si leur distance vaut 1. Le problème de Hadwiger-Nelson est alors de déterminer le nombre chromatique de G, c'est pourquoi ce problème est souvent décrit comme la question de « déterminer le nombre chromatique du plan ». Le théorème de De Bruijn-Erdős montre qu'en admettant l'axiome du choix, la question revient à déterminer le plus grand nombre chromatique d'un graphe planaire distance-unité fini. La question est aussi équivalente à déterminer le plus petit entier n pour lequel il existe une partition du plan telle qu'aucun des ne contienne de couples de points séparés d'une unité[6] ; sous cette forme, on peut exiger que les aient des propriétés géométriques supplémentaires, simplifiant le problème, comme analysé ci-dessous.

Bornes[modifier | modifier le code]

Le graphe de Solomon W. Golomb, un graphe distance-unité 4-chromatique ayant dix sommets.

La façon la plus simple d'obtenir une borne supérieure à la solution consiste à exhiber une coloration du plan satisfaisant à l'énoncé ; de même, une borne inférieure k est obtenue en exhibant un contre-exemple, c'est-à-dire un graphe distance-unité de nombre chromatique k.

Jusqu'en 2018, on n’avait pas découvert de graphe distance-unité de nombre chromatique supérieur à 4. Le premier exemple d’un graphe 4-chromatique fut découvert en 1961 par les frères William et Leo Moser, un graphe à 7 sommets appelé le fuseau de Moser. Un autre graphe (à 10 sommets) fut découvert à peu près en même temps par Solomon W. Golomb, mais il ne le publia pas immédiatement[7].

Cependant, en , des graphes de nombre chromatique 5 (comportant plusieurs milliers de sommets, le plus petit a 1581 sommets) ont été découverts par Aubrey de Grey et contrôlés par ordinateur[8],[9].

La borne supérieure provient de l'existence d'un pavage du plan par des hexagones réguliers de diamètre un peu inférieur à 1, que l'on peut colorier périodiquement en 7 couleurs (cette coloration est connue sous le nom de carte de Heawood[10]), ce qui fut remarqué par John R. Isbell[Quand ?][11].

Il a souvent été remarqué que le problème de Hadwiger-Nelson est non seulement d'énoncé simple, mais que les meilleures bornes connues (jusqu'en 2018) reposaient sur des exemples et contre-exemples tout à fait élémentaires, rendant exaspérante l'absence de progrès faits vers sa résolution en plus d'un demi-siècle[5],[12].

Variantes du problème[modifier | modifier le code]

Le problème se généralise facilement aux dimensions supérieures. Comme pour le plan, le « nombre chromatique de l'espace » (à trois dimensions) n'est pas connu, mais on sait qu'il est compris entre 6 et 15[13].

On peut aussi imposer aux ensembles de points d'une même couleur de devoir satisfaire une condition supplémentaire[14]. Cela rend certaines colorations inacceptables, ce qui peut augmenter le nombre de couleurs requises. Ainsi, si l'on demande que tous ces ensembles soient mesurables au sens de Lebesgue, on savait (longtemps avant les découvertes de 2018) que cinq couleurs au moins sont nécessaires. Il existe des modèles de la théorie des ensembles (par exemple le modèle de Solovay (en)) dans lesquels tous les sous-ensembles du plan sont mesurables, et donc dans ces modèles le nombre chromatique du plan est au moins cinq ; c’est ce résultat qui fait penser que la réponse pourrait dépendre de l’axiome du choix[15]. Si l'on demande que les ensembles soient formés de régions ayant pour frontières des courbes de Jordan, six couleurs au moins sont nécessaires[16].

Il est enfin possible de se limiter à certains sous-ensembles de points du plan, par exemple aux points à coordonnées rationnelles ; on dispose souvent de résultats exacts dans ce cas[10].

Voir aussi[modifier | modifier le code]

Notes[modifier | modifier le code]

  1. ↑ Jensen et Toft 1995
  2. ↑ Gardner 1960
  3. ↑ Hadwiger 1945
  4. ↑ Hadwiger 1961
  5. ↑ a et b Soifer 2008, chapitres 2 et 3.
  6. ↑ Coulson 2004
  7. ↑ Soifer 2008, p. 19.
  8. ↑ Aubrey D.N.J. de Grey, The chromatic number of the plane is at least 5 (en).
  9. ↑ David Madore, Le progrès récent sur le problème de Hadwiger-Nelson.
  10. ↑ a et b Madore 2015
  11. ↑ Soifer 2008
  12. ↑ Madore 2012
  13. ↑ Coulson 2002; Radoičić et Tóth 2003.
  14. ↑ Voir, par exemple, Croft, Falconer et Guy 1991.
  15. ↑ Soifer 2008, pp. 557–563; Shelah et Soifer 2003
  16. ↑ Woodall 1973 ; voir aussi Coulson 2004 pour une autre démonstration d'un résultat analogues.

Références[modifier | modifier le code]

  • (en) N. G. de Bruijn et P. Erdős, « A colour problem for infinite graphs and a problem in the theory of relations », Nederl. Akad. Wetensch. Proc. Ser. A, vol. 54,‎ , p. 371–373.
  • (en) K. B. Chilakamarri, « The unit-distance graph problem: a brief survey and some new results », Bull Inst. Combin. Appl., vol. 8,‎ , p. 39–60.
  • (en) Kiran B. Chilakamarri et Carolyn R. Mahoney, « Unit-distance graphs, graphs on the integer lattice and a Ramsey type result », Aequationes Mathematicae, vol. 51, nos 1-2,‎ , p. 48–67 (DOI 10.1007/BF01831139, MR 1372782).
  • (en) D. Coulson, « On the chromatic number of plane tilings », J. Austral. Math. Soc., vol. 77, no 2,‎ , p. 191–196 (DOI 10.1017/S1446788700013574, lire en ligne).
  • (en) D. Coulson, « A 15-colouring of 3-space omitting distance one », Discrete Math., vol. 256,‎ , p. 83–90 (DOI 10.1016/S0012-365X(01)00183-2).
  • (en) Hallard T. Croft, Kenneth J. Falconer et Richard K. Guy, Unsolved Problems in Geometry, Springer-Verlag, , Problem G10.
  • (en) Martin Gardner, « Mathematical Games », Scientific American, vol. 203/4,‎ , p. 180.
  • (en) Hugo Hadwiger, « Überdeckung des euklidischen Raumes durch kongruente Mengen », Portugal. Math., vol. 4,‎ , p. 238–242.
  • (en) Hugo Hadwiger, « Ungelöste Probleme No. 40 », Elem. Math., vol. 16,‎ , p. 103–104.
  • (en) Tommy R. Jensen et Bjarne Toft, Graph Coloring Problems, Wiley-Interscience Series in Discrete Mathematics and Optimization, , 150–152 p..
  • (en) Michael S. Payneg, « Unit distance graphs with ambiguous chromatic number », The Electronic Journal of Combinatorics,‎ (lire en ligne)
  • (en) Radoš Radoičić et Géza Tóth, Discrete and Computational Geometry : The Goodman–Pollack Festschrift, vol. 25, Berlin, Springer, coll. « Algorithms and Combinatorics », , 695–698 p. (DOI 10.1007/978-3-642-55566-4_32, MR 2038498, lire en ligne), « Note on the chromatic number of the space ».
  • (en) Saharon Shelah et Alexander Soifer, « Axiom of choice and chromatic number of the plane », Journal of Combinatorial Theory, Series A, vol. 103, no 2,‎ , p. 387–391 (DOI 10.1016/S0097-3165(03)00102-X, lire en ligne).
  • (en) Alexander Soifer, The Mathematical Coloring Book : Mathematics of Coloring and the Colorful Life of its Creators, New York, Springer, (ISBN 978-0-387-74640-1),
  • (en) D. R. Woodall, « Distances realized by sets covering the plane », Journal of Combinatorial Theory, vol. 14,‎ , p. 187–200 (DOI 10.1016/0097-3165(73)90020-4, MR 0310770)

Liens externes[modifier | modifier le code]

Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Problème_de_Hadwiger-Nelson&oldid=207719358 ».